Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПЛАЗМЕННО-ГИДРОДИНАМИЧЕСКАЯ КОНЦЕПЦИЯ СОСТОЯНИЯ ИОНОВ В РАСТВОРАХ ЭЛЕКТРОЛИТОВ В ОЦЕНКЕ НЕКОТОРЫХ СВОЙСТВ

Балданова Д М, Танганов Б Б,

3.3. Определение радиусов гидратированных ионов

В основе современных методов определения радиусов сольватированных ионов лежат представления Стокса, согласно которым радиусы макроскопических частиц, движущихся в идеальной гидродинамической среде, определяются по экспериментальным предельным значениям электропроводности  и вязкости  [82]:

,

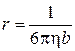где  – подвижность ионов, выраженная через предельную электропроводность согласно уравнению .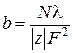

Полученные таким образом стоксовские радиусы более реальны для ионов с большими значениями кристаллографических радиусов, чем для частиц с меньшими размерами.

Использование правила Вальдена-Писаржевского, основанного на постулировании постоянства произведения  при условии, что и радиус иона остается постоянным так же не является универсальным, так как радиусы сольватированных ионов в различных средах имеют разные значения.

Согласно развиваемой нами концепции состояния ионов в растворах элект­ролитов, возможный вариант решения данной задачи состоит в рам­ках стандартных положений электродинамики и механики [83].

Предварительно рассматриваются все ионы, не участвующие в эста­фетном механизме переноса заряда. В качестве основы принимается кулоновский потенциал системы распределенных зарядов:

,                                          (3.6)

где  – плотность зарядов;  – элементарный заряд;  – плотность числа частиц в 1 см³ объема;  – расстояние от системы зарядов в элементарном объеме  до точки наблюдения. В качестве элементарного объема  примем объем сольватированного иона, равный . В этом случае точку наблюдения можно взять на поверхности объема , тогда  [84]. Тогда

.

.

Таким образом, интегрирование уравнения (3.6) приводит к выра­же­нию, определяющему энергию взаимодействия иона с  молекулами растворителя в виде:

,                                        (3.7)

где 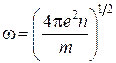 – частота ленгмюровских плазменных колебаний.

Если же гидратированный ион рассматривать как систему точечных зарядов, то энергию в виде уравнения (3.7) можно представить в форме

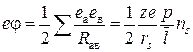,                             (3.8)

где  – заряд иона;  – дипольный заряд молекулы воды; p – дипольный момент молекулы воды;  – дипольное расстояние;  – радиус гидратированного иона;  – гидратное число.

Следовательно, равенство представлений (3.7) и (3.8) в виде:

,

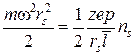приводит к следующему выражению:

.

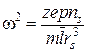Тогда соответствующая энергия этих колебаний плотности заряда относительно ее равновесного значения равна:

.

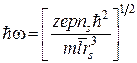Граница гидратного комплекса определяется условием , где правая часть является кинетической энергией молекул воды:

.

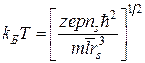Таким образом, выражение для теоретических оценок радиусов гидратированных ионов принимает следующий вид:

.

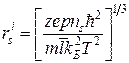Подставив в данное уравнение значения всех универсальных постоянных и параметры воды p,  в системе единиц СГС, получаем следующее выражение [83]:

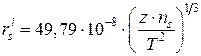, см.                       (3.9)

Некоторые результаты теоретических оценок радиусов гидратированных ионов по уравнению (3.9) и их сопоставление с данными Стокса [85] приведены в табл. 3.2.

Таблица 3.2

Радиусы гидратированных ионов