Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Балданова Д М, Танганов Б Б,
3.4. Определение радиусов гидратированных ионов и и эстафетный механизм их переноса в растворах
Теория эффективных радиусов 
и 
в растворах электролитов коренным образом отличается от таковых для других ионов. Это связано с тем, что процессы переноса в водных растворах кислот и оснований (электропроводность, вязкость, диффузия и теплопроводность) имеют характер эстафетного механизма [4]:
(3.10)
. (3.11)
В процессе (3.10) ионы группируют 4 молекулы воды [86]. При этом отрицательные заряды диполей воды направлены к , что облегчает туннельный переход протона 
в к молекулам воды и далее.
В случае процесса (3.11), ионы ориентируют 2 молекулы 
положительными зарядами диполей. Тогда за счет туннельного эффекта ионы из переходят к иону .
Эти процессы и объясняют аномально высокую подвижность и электропроводность растворов кислот и оснований.
Эффективные радиусы этих гидратированных ионов формализуются известной задачей механики [72] о системе, состоящей из одной частицы с массой 
и 
частиц с одинаковыми массами 
.
Если исключить движение центра инерции, то проблема сводится к задаче движения частиц с – масса ионов или ; – масса молекул воды; 
– гидратное число.
Рассматривается гидратный комплекс, в котором 
– радиус-вектор или ; 
– радиус вектор гидратированных молекул воды в гидратном комплексе. Расстояние от или до молекул в этом комплексе обеспечивается выражением:
, (3.12)
а начало координат в центре инерции формализуется равенством:
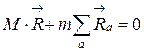. (3.13)
Очевидно, введение в уравнение (3.13) значения из [87] дает безразмерное равенство в оригинальной постановке задачи
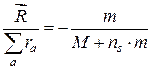. (3.14)
Гидратированные ионы имеют центрально-симметричное распределение вещества и заряда, и при их движении под действием внешнего поля меняется система отсчета. Тогда возможно умножение левой и правой частей уравнения (3.14) на величину
. Далее, в левую часть уравнения (3.14) вводится значение 
из выражения (3.12), что приводит к следующему уравнению:
.
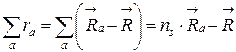В этом случае
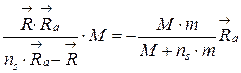. (3.15)
Наглядная трансформация векторных величин к их скалярам в виде модулей возможна в виде
.
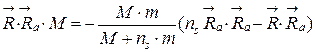Угол между векторами 
и равен α = 180°, а между векторами и α = 0°. Тогда, согласно правилам векторного анализа, скалярное произведение двух векторов равно произведению их модулей на 
(где α – угол между направлениями этих векторов). Поэтому 
, так как 
и 
ввиду того, что 
.
Приведенные факты дают основание следующему представлению
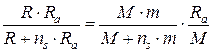. (3.16)
Таким образом, приведенная симметричная форма выражения (3.16) в скалярных аргументах с учетом приведенной массы системы, равной
,
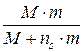показывает, что
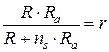
Представляет собой эффективный приведенный радиус системы.
Радиус молекулы воды в жидком состоянии при 298 K равен R = 1,15×10-8 см [4], радиус 
= 1,35×10-8 см [87] и радиус 
= 1,53×10-8 см [87]. Далее, гидратное число 
= 4 [86] и 
= 2,2 из уравнения (3.16) при 
= 1,53×10-8.
При этих значениях R, и эффективные радиусы ионов и равны:
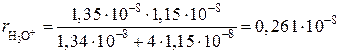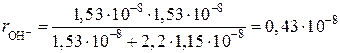см,
см.
Полученные значения 
и 
используются для кислот и оснований.