
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.5. Методы определения термодинамических характеристик сольватации ионов
Прямое измерение данных термодинамических характеристик принципиально неосуществимо. В настоящее время, нахождение характеристик процессов гидратаций ионов в основном основано на делении соответствующих экспериментально найденных термохимических характеристик для стехиометрических смесей ионов в растворе на ионные составляющие. Полученные таким способом термодинамические характеристики ионов являются в значительной степени неопределенными и зависят от физической обоснованности выбранного метода деления.
Первой серьезной попыткой в разработке теоретического метода вычисления термодинамических характеристик гидратации, основанной на модели среды как непрерывного диэлектрика, является работа Борна [88]. Он получил выражение для вычисления изменения энтальпии при гидратации ионов, известное под названием Борна-Бьеррума:
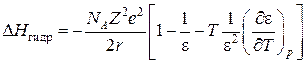 ,
,
где ![]() – радиус жесткой сферы иона;
– радиус жесткой сферы иона; ![]() – заряд иона;
– заряд иона; ![]() – диэлектрическая постоянная среды;
– диэлектрическая постоянная среды; ![]() – температура;
– температура; ![]() – постоянная Авогадро.
– постоянная Авогадро.
Усовершенствование теории Борна идет по пути уточнения радиусов ионов в водных растворах; учета изменения диэлектрической постоянной воды вблизи иона по аналогии с изменением ее под действием давления, введения дополнительных членов, комбинированного устранения указанных недостатков и т.д.
Так, Уэбб ввел поправки на уменьшение диэлектрической постоянной раствора и на работу сжатия растворителя в поле иона [89]. Вместе с тем теория Уэбба по-прежнему рассматривает растворитель как непрерывную среду и не учитывает строение его молекул и структуру.
К числу удачных работ этого направления следует отнести исследования Стокса, согласно которым суммарная энергия гидратации делится на электростатическую и неэлектростатическую составляющие. Первую он рассчитывал на основе модели Борна, вводя поправки на изменение диэлектрической постоянной вблизи иона и используя вместо кристаллохимических вандерваальсовы радиусы [88].
Чтобы отказаться от представлений о растворителе как о некоторой сплошной и однородной среде, необходимо учитывать индивидуальные свойства ее молекул. Одна из первых теорий, основанных на модельных представлениях, принадлежит Ван-Аркелю [89]. Он ввел представления об ион-дипольном характере взаимодействия при гидратации ионов, что позволило отказаться от понятия среды, как континуума, и учесть свойства отдельных молекул воды (их дипольные моменты, поляризуемость и т.д.).
Новые пути теоретического расчета термодинамических характеристик гидратации основываются на идеях, развитых Берналлом и Фаулером [89]. Сущность их теории сводится к расчету указанных величин с учетом строения молекул воды, по крайней мере, тех, что расположены по соседству с ионом. В упомянутой работе энергия гидратации состоит из ряда составляющих. Первая характеризует взаимную энергию иона и молекул воды с некоторыми поправками. Вторая пытается учесть изменение энергии при взаимодействии иона с первым слоем молекул воды. Третья учитывает энергию взаимного отталкивания молекул воды в гидратной оболочке. Следует отметить, что из-за произвольных допущений, корректный расчет тепловых эффектов гидратации по этому методу невозможен.
Последовательные улучшения ввели Эли и Эванс, Фервей, Элли и Пеппер , Мелвин-Хьюз, Дракин и Михайлов [89].
Характерным примером работ этого направления является исследование Бакингема [90]. Согласно которому, зависимость энергии взаимодействия иона с молекулами воды от величины, обратной расстоянию между центром иона и молекулами растворителя, выражается степенным рядом. Но в работе Бакингема не оценен энергетический эффект «химической» составляющей взаимодействия и отсутствует оценка сил отталкивания.
Мищенко и Сухотин [88] предложили метод расчета химических теплот гидратаций ![]() , который более полно учел составляющие эффекты взаимодействия при гидратации ионов. Авторы учли ассиметрию диполя молекулы воды, что позволило, в свою очередь, учесть различие в гидрофильности катионов и анионов одинакового заряда и радиусов.
, который более полно учел составляющие эффекты взаимодействия при гидратации ионов. Авторы учли ассиметрию диполя молекулы воды, что позволило, в свою очередь, учесть различие в гидрофильности катионов и анионов одинакового заряда и радиусов.
Можно отметить работы Аззама [89], в которых кроме борновской энергии на основе структурных предпосылок учитываются вклады, относящиеся к образованию первичной и вторичной сольватных оболочек. Определенный интерес вызывают работы Мюхид-Голд и Лайдлера [89], которыми в приближении Эли-Эванса рассчитаны изменения энтальпии при сольватации ионов. В уравнении учтено распределение зарядов в молекуле воды и использована ее поляризационно-дипольная модель.
Развиваются и теоретические методы определения энергетических характеристик сольватации ионов на основе методов статистической термодинамики и квантово-химических расчетов всех видов взаимодействия в растворах. Примером первых из них могут служить исследования Юхновского с сотрудниками [91]. Ими выдвинута микроскопическая теория растворов электролитов, учитывающая короткодействующие и дальнодействующие взаимодействия на основе коллективных переменных. Развиваемые представления открывают принципиальные возможности количественного описания растворов в зависимости от концентрации электролитов и свойств растворителя в широкой области термодинамических параметров.
На данном этапе развития теории растворов и накопления экспериментального материала, энергетические характеристики сольватации ионов находят путем деления экспериментально найденных суммарных величин на ионные составляющие с последующей обработкой их на основе приближенных корреляций.
Так Ланге и Мищенко [88] в основу разделения ![]() на ионные составляющие положили допущение о равенстве изменений энтальпии при гидратации ионов
на ионные составляющие положили допущение о равенстве изменений энтальпии при гидратации ионов ![]() и
и ![]() . Для этой цели они использовали представления об асимметрии диполя молекулы воды, согласно которым последние при гидратации располагаются ближе к анионам, чем к катионам. Фактор асимметрии, найденный авторами, колеблется в пределах 0,022–0,028 нм. Поэтому расстояние между центрами положительных и отрицательных ионов одинакового заряда и размера и центром диполя воды должно отличаться на удвоенное значение этой величины. Разность кристаллохимических радиусов ионов
. Для этой цели они использовали представления об асимметрии диполя молекулы воды, согласно которым последние при гидратации располагаются ближе к анионам, чем к катионам. Фактор асимметрии, найденный авторами, колеблется в пределах 0,022–0,028 нм. Поэтому расстояние между центрами положительных и отрицательных ионов одинакового заряда и размера и центром диполя воды должно отличаться на удвоенное значение этой величины. Разность кристаллохимических радиусов ионов ![]() и
и ![]() обеспечивает взаимную компенсацию в различных размерах ионов. Этому условию, в зависимости от выбранной системы кристаллохимических радиусов ионов, отвечают также другие пары изозарядных, изоэлектронных ионов и ионов благородных газов, например,
обеспечивает взаимную компенсацию в различных размерах ионов. Этому условию, в зависимости от выбранной системы кристаллохимических радиусов ионов, отвечают также другие пары изозарядных, изоэлектронных ионов и ионов благородных газов, например, ![]() и
и ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]() . Здесь решающее значение имеет тот факт, что вклад неэлектрического взаимодействия в
. Здесь решающее значение имеет тот факт, что вклад неэлектрического взаимодействия в ![]() уменьшается при переходе от иона лития к иону цезия и от фтор – к иод-иону. Это обстоятельство приводит дополнительно к выравниванию гидрофильности ионов
уменьшается при переходе от иона лития к иону цезия и от фтор – к иод-иону. Это обстоятельство приводит дополнительно к выравниванию гидрофильности ионов ![]() и
и ![]() в водных растворах. Более полный критический обзор существующих методов деления дан в работе [88].
в водных растворах. Более полный критический обзор существующих методов деления дан в работе [88].
Однако следует отметить, что полученные таким образом величины ![]() имеют приближенные значения, связанные с
имеют приближенные значения, связанные с
различного рода допущениями при делении на ионные составляющие. Отсутствует согласование между различными термодинамическими характеристиками гидратации отдельных ионов. Существуют трудности применения данных величин для смешанных растворителей.
