
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.7. Кинетический анализ процессов равновесий диссоциации растворов электролитов, плазменная частота и энергия многочастичных взаимодействий
Для рассмотрения вопросов, связанных с процессами переноса в качестве исходной предпосылки воспользуемся рассмотренным выше равновесным процессом диссоциации некоторого электролита ![]() в произвольном растворителе
в произвольном растворителе
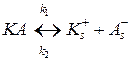 , (3.21)
, (3.21)
где ![]() и
и ![]() – константы скоростей;
– константы скоростей; ![]() и
и ![]() – сольватированные катион и анион. При фиксированной концентрации вещества
– сольватированные катион и анион. При фиксированной концентрации вещества ![]() средняя длина свободного пробега ионов
средняя длина свободного пробега ионов ![]() и
и ![]() конечна. Согласно общим положениям механики, любое одномерное конечное движение есть колебательное. Для раскрытия физического содержания этих колебаний необходимо провести кинетический анализ диссоциации процесса равновесия (3.21).
конечна. Согласно общим положениям механики, любое одномерное конечное движение есть колебательное. Для раскрытия физического содержания этих колебаний необходимо провести кинетический анализ диссоциации процесса равновесия (3.21).
Данный процесс характеризует система уравнений:
|
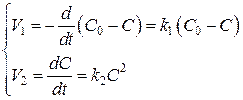 (322а)
(322а)
где ![]() – начальная концентрация электролита;
– начальная концентрация электролита; ![]() – концентрация диссоциированных молекул электролита;
– концентрация диссоциированных молекул электролита; ![]() – концентрация недиссоциированных молекул.
– концентрация недиссоциированных молекул.
Данная система уравнений предполагает два различных варианта анализа для сильных и слабых электролитов, главными критериями, которых являются следующие условия:
1) для сильных электролитов ![]() ;
;
2) для слабых электролитов ![]() .
.
Приведенная система уравнений соответствует общим положениям понятия химического равновесия. Так, при ![]() (3.22) получаем константу равновесия:
(3.22) получаем константу равновесия: 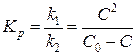 , соответствующую закону разбавления Оствальда. При этом структура уравнения (3.21) предполагает использование критерия устойчивости по Ляпунову. По данному критерию, некоторая произвольная функция
, соответствующую закону разбавления Оствальда. При этом структура уравнения (3.21) предполагает использование критерия устойчивости по Ляпунову. По данному критерию, некоторая произвольная функция ![]() непрерывно дифференцируема, для которой выполняются следующие условия:
непрерывно дифференцируема, для которой выполняются следующие условия: ![]() > 0 при y ¹ 0,
> 0 при y ¹ 0, ![]() при y = 0
при y = 0
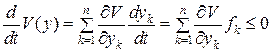 . (3.23)
. (3.23)
Для исследуемой системы уравнений (3.23), параметр ![]() соответствует концентрации
соответствует концентрации ![]() . При кинетическом анализе равновесия диссоциации некоторого электролита представляется интересным второй вариант последнего условия (3.23), когда возможны асимптотические устойчивости и вероятны предельные циклы на фазовой плоскости [93].
. При кинетическом анализе равновесия диссоциации некоторого электролита представляется интересным второй вариант последнего условия (3.23), когда возможны асимптотические устойчивости и вероятны предельные циклы на фазовой плоскости [93].
Данное требование предполагает исследование условия критерия (3.23) для производной по времени от скорости ![]() в представлении (3.22), обеспечивающим генерацию ионов:
в представлении (3.22), обеспечивающим генерацию ионов:
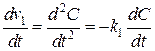 . (3.24)
. (3.24)
Поскольку скорости ![]() и
и ![]() в (3.22а) и (3.22б) являются сопряженными величинами, то в (3.24) вместо
в (3.22а) и (3.22б) являются сопряженными величинами, то в (3.24) вместо ![]() можно взять его значение для
можно взять его значение для ![]() из (3.22б). Тогда:
из (3.22б). Тогда:
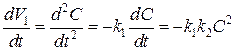 . (3.25)
. (3.25)
Так как ![]() , возможно представить выражение (3.24) в виде:
, возможно представить выражение (3.24) в виде:
![]() . (3.26)
. (3.26)
Для сильных электролитов, можно пренебречь вторым слагаемым в правой части. Тогда при ![]() , имеет место:
, имеет место:
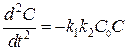 . (3.27)
. (3.27)
А это есть уравнение гармонических колебаний с решением
![]() . (3.28)
. (3.28)
По существу уравнение (3.28) является частотой популяционных колебаний Лотка-Вольтерра [94]. Определим в (3.28) значения констант скоростей ![]() и
и ![]() .
.
Решение этой задачи возможно в рамках обеспечения законов сохранения массы и заряда с использованием уравнения непрерывности
![]() . (3.29)
. (3.29)
Плотность массы или заряда ![]() может быть представлена через молярную концентрацию в следующем виде
может быть представлена через молярную концентрацию в следующем виде ![]() , где
, где ![]() – число Авогадро и 1000 – размерный коэффициент перехода от миллилитров к литрам.
– число Авогадро и 1000 – размерный коэффициент перехода от миллилитров к литрам.
Подставляя данное выражение в (3.29), после сокращения на постоянный множитель ![]() , получаем:
, получаем:
![]() . (3.30)
. (3.30)
В электродинамике первым двум слагаемым соответствует полная производная:
![]() . (3.31)
. (3.31)
Учитывая выражение (3.31) в (3.30) получаем:
![]() .
.
Для этого выразим (2.18а) и (2.18б) в удобных для сравнения видах.
|
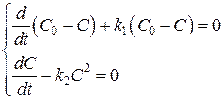 (332)
(332)
|
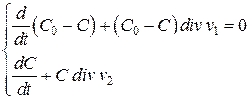 (334)
(334)
Из уравнений (3.32) и (3.34) выразим значение ![]() , а из (3.33) и (3.35) значение
, а из (3.33) и (3.35) значение ![]() , где
, где ![]() – скорость движения при диссоциации и v2 – скорость движения при рекомбинации ионов.
– скорость движения при диссоциации и v2 – скорость движения при рекомбинации ионов.
В равновесных условиях скорость взаимного удаления сольватированных ионов друг от друга ![]() в уравнении (3.21) при диссоциации
в уравнении (3.21) при диссоциации ![]() должна быть равной скорости их сближения
должна быть равной скорости их сближения ![]() при обратной ассоциации их в ионные двойники.
при обратной ассоциации их в ионные двойники.
Поскольку выражение (3.28) является частотой гармонических колебаний, то имеет место операторное тождество
![]() , (3.36)
, (3.36)
где ![]() – волновое число.
– волновое число.
Подставим в (3.28) значения ![]() и
и ![]() с учетом (3.36):
с учетом (3.36):
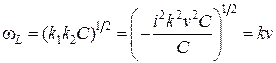 . (3.37)
. (3.37)
Здесь волновое число ![]() и тепловая скорость [95]:
и тепловая скорость [95]:
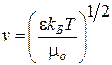 . (3.38)
. (3.38)
Дебаевский радиус для растворов электролитов равен [96]:
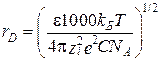 . (3.39)
. (3.39)
Подставляя уравнения (3.38) и (3.39) в формулу (3.37) получим уравнение для плазменной частоты:
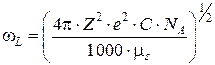 . (3.40)
. (3.40)
Таким образом, показано, что в растворах электролитов возможно локальное изменение плотности заряда с плазменной частотой (3.40). Определить же потенциальную энергию таких коллективных многочастичных взаимодействий системы ионов можно на основании кулоновского потенциала ![]() для распределенного заряда по элементу объема
для распределенного заряда по элементу объема ![]() , рассмотренного выше:
, рассмотренного выше:
![]() . (3.6)
. (3.6)
Если задать условие нахождения ![]() внутри объема
внутри объема ![]() , полагая
, полагая ![]() , тогда, при
, тогда, при ![]() , возможно представление:
, возможно представление:
![]() .
.
Отсюда, потенциальная энергия ![]() приобретает вид:
приобретает вид:
![]() .
.
Умножим и разделим правую часть на приведенную массу ![]() электролита:
электролита:
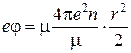 ,
,
где 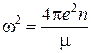 – квадрат ленгмюровской плазменной частоты [97].
– квадрат ленгмюровской плазменной частоты [97].
Тогда, согласно [98]:
![]()
есть потенциальная энергия осциллятора. По определению ![]() . В этом случае возможно следующее представление:
. В этом случае возможно следующее представление:
![]()
![]()
где ![]() – импульс и
– импульс и ![]() – классический предел соотношения неопределенностей Гейзенберга. Поэтому,
– классический предел соотношения неопределенностей Гейзенберга. Поэтому,
![]() , (3.41)
, (3.41)
где ![]() – полная энергия плазменных колебаний.
– полная энергия плазменных колебаний.
Таким образом, результаты, полученные на основании кинетического анализа процесса равновесия (3.21), свидетельствует, что сольватированные ионы, совершающие колебательные движения, дают возможность использования силы вязкости:
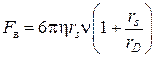 (3.42)
(3.42)
для получения уравнения электропроводности через подвижность ![]() .
.
