Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

2.3.3. Изопериметрические соотношения

В геометрических экстремальных задачах симметрия проявляется в изопериметрических задачах. В качестве иллюстрации приведем пример формулировок теорем для нескольких изопериметрических задач на плоскости.

Среди всех простых замкнутых кривых заданной длины наибольшую площадь ограничивает окружность.

Заметим, что площадь  всякой фигуры, периметр которой равен , удовлетворяет так называемому изопериметрическому неравенству на плоскости: .

Среди всех - мерных параллелепипедов одинакового объема наименьший периметр имеет - мерный куб (см. рис.2.4).

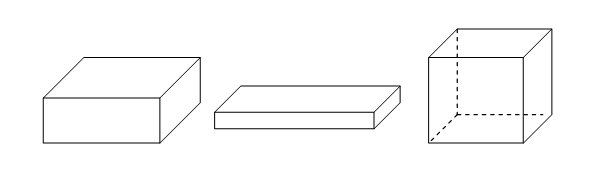
Рисунок 2.4. 3-мерные параллелепипеды одинакового объёма

Среди всех -угольников, описанных около окружности, наименьшую площадь имеет правильный -угольник.

Рассмотрим одну задачу сначала в геометрической, а затем в алгебраической постановках.

Задача о делении линии.Требуется разделить линию длиной  единиц на  отрезков, так, чтобы длина каждого отрезка равнялась целому числу единиц, а произведение длин отрезков было максимальным. Этот пример относится к особому классу задач, к изучению которого мы переходим.