Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В СРЕДЕ DELPHI

Кирьянов Б Ф,

ВВЕДЕНИЕ. Общие сведения о математических моделях и математическом моделировании. Среда Delphi как средство моделирования

1. Понятие системы. Методы исследования систем. Система – это совокупность объектов, функционирующих и взаимодействующих друг с другом для достижения определённой цели. В ряде случаев проводить эксперименты можно на реальных системах. Однако далеко не всегда это возможно, например, при невозможности получения строгого математического описания системы. Поэтому в таких случаях создаются модели реальных систем, которые и исследуются (слово «модель» происходит от греческого слова modulus). Выявленные в процессе исследования характеристики модели приписываются реальной системе, то есть системе-оригиналу. Исследования, проводимее на модели, и называются моделированием [9, 48, 62 и др.].

2. Общие определения модели и моделирования. Отметим: никакое определение не может в полном объёме охватить реально существующую деятельность по моделированию. Однако определения полезны тем, что в них делается попытка выделить наиболее существенные черты моделей и моделирования.

Свободная международная энциклопедия – википедия: Моделирование – исследование объектов познания на их моделях, построение и изучение моделей реально существующих предметов, процессов или явлений с целью получения объяснений этих явлений, а также для их предсказания.

Ляпунов А.А.: Моделирование – это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель).

Советов Б.Я. и Яковлев С.А.: Модель – это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала [62].

3. Разновидности моделей. Модели принято делить на два класса: физические и математические. Физические модели имеют ту же физическую природу, что и оригинал. Физической моделью является, например, аэродинамическая труба, в которой устанавливается самолёт для исследования поведения его органов управления при продувании трубы воздухом с такой же скоростью, как при реальном полёте. Физическим моделированием являются испытания опытных образцов различной аппаратуры на тряску, давление и т.д. Математическая модель – это точное или приближённое математическое описание свойств или закономерностей функционирования оригинала.

4. Определения математической модели и моделирования

Самарский А.А. и Михайлов А.П.: Математическая модель – это «эквивалент объекта, отражающий в математической форме важнейшие его свойства – законы, которым он подчиняется, связи, присущие составляющим его частям». «Математическое моделирование – процесс построения и изучения математических моделей реальных процессов и явле- ний» [61].

Севостьянов А.Г.: Математической моделью называется совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе.

Скворцова М.: Математическая модель – это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная задача математического моделирования – не только исследовать эти объекты, но и предсказать результаты будущих наблюдений.

В целом в литературе довольно много похожих определений. Самое короткое и лаконичное определение модели дано в одной из зарубежных публикаций: Математическая модель это Уравнение, выражающее идею. Но это определение относится, скорее, к философскому понятию модели.

5. Немного истории. Исследование систем путем их моделирования. Ещё во 2-м веке до н.э. появилась геоцентрическая система (модель) мира Птоломея, затем − гелиоцентрическая система (модель) мира Николая Коперника (16-й век н.э., helio – приставка, означающая солнце). С развитием техники перед изготовлением паровых машин, электрических установок, средств автоматизации вычислений и т.д. в большинстве случаев они предварительно отрабатывались на их моделях. Предварительное моделирование особенно важно проводить при разработке новых перспективных производственных технологий для обеспечения их эффективности, сложной и дорогостоящей техники для обеспечения её надежности (например, надёжности нового космического корабля) и т.д.

В 20-м веке с появлением ЭВМ активизировались разработка математических моделей и методов и технологий математического моделирования на ЭВМ. При этом установилась классификация способов исследования систем с помощью моделей [48, 62 и др.], приведённая на рис. В.1.

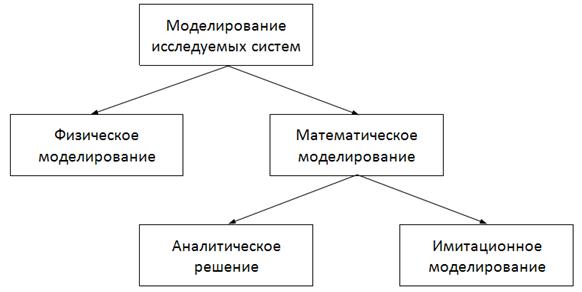
Рис. В.1. Способы исследования систем

В отличие от физического моделирования, предполагающего измерение соответствующих характеристик модели, математическое моделирование предполагает разработку математического описания функционирования исследуемой системы, которое в ряде случаев может иметь аналитическое решение. При имитационном моделировании на основе алгоритмов, описывающих указанное функционирование, модель воспроизводит процессы, происходящие в реальной системе. Частным случаем этого моделирования является эволюционное моделирование, связанное с исследованием эволюции различных систем [57].

6. Понятия функциональной полноты и адекватности модели. Пусть некоторый оригинал (рис. В.2) имеет k входов, на которые поступают соответствующие входные величины, задаваемые вектором X = (X₁, X₂, … X_k). Аналогично выходы оригинала задаются вектором Y = (Y₁, Y₂, … Y_k).

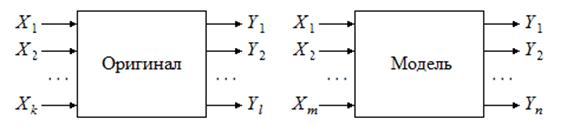
Рис. В.2. Абстрактная система оригинал – модель

Каждая координата Y_i является функцией вектора X и внутреннего состояния оригинала. Последнее в общем случае может изменяться под воздействием как входных, так и выходных величин. Если на вход модели поступает последовательность векторов X, то имеют место векторные процессы X(t) и Y(t), которые могут быть детерминированными или случайными.

Как и оригинал, модель может иметь k входов и l выходов, формируе-мых0аналогично0оригиналу. Такая модель называется функционально полной. Если при этом имеет место ещё0и0полное0совпадение выходных процессов модели и её оригинала, соответствующих любому входному процессу, то говорят, что модель адекватна оригиналу. Однако во многих случаях при моделировании нет необходимости воспроизводить все возможности оригинала. В этом случае выбирают m < k и n < l и нередко говорят о степени адекватности построенной модели по отношению к оригиналу. Однако заметим, что понятие «степень адекватности», а также используемые в литературе такие характеристики этой степени как «высокая степень адекватности», «достаточно адекватная» или «относительно адекватная», количественно не определены. Поэтому с математической точки зрения они несостоятельны. Использование же их объясняется тем, что нередко адекватность модели оригиналу просто невозможно проверить (например, ввиду ограниченности технических возможностей и т.д.).

Основные этапы разработки математических моделей:

·         Разработка математического описания предварительного варианта модели (уточнение задачи моделирования, определение требований к входным и выходным переменным, построение структурной схемы модели, выбор её параметров, выбор методов получения конечных и промежуточных результатов). Результатом этого этапа является формальное математическое описание блоков модели. При этом как бы исчезает физическая сторона исследуемой задачи, то есть для лиц, не знакомых с решаемой задачей, по математическому описанию модели крайне затруднительно или даже невозможно уяснить сущность этой задачи.

style=font-family:Symbol>·         Разработка машинной программы моделирования, включая алгоритмизацию математического описания, разработку программы в соответствующей среде программирования и проверку правильности её работы (например, по моделированию характерных частных вариантов входных величин, для которых известны или могут быть рассчитаны значения выходных величин).

·         Испытания и корректировка модели (моделирование исследуемой системы для известных частных случаев, сравнение получаемых при этом результатов с известными результатами и в случае необходимости – корректировка параметров модели). Данный этап часто называют интерпретацией результатов моделирования.

Разработка модели при отсутствии оригинала. Примером такой модели может служить модель интегральных показателей (ИП) здоровья населения, использующая в качестве параметров показатели здоровья населения. Эти показатели ежегодно определяются и публикуются Госкомстатом России. Основным вариантом таких моделей является следующий [42]:

ИП = К₁ОКР + К₂СППЖ – К₃ОЗО – К₄ПИНВ – К₅ОКС + С,

где K_I – весовые коэффициенты, ОКР – общий коэффициент рождаемости (число родившихся живыми младенцев, приходящихся на 1000 человек населения рассматриваемого региона), СППЖ – средняя продолжительность предстоящей жизни (значение прогноза, определяемого для поколения, родившегося в рассматриваемом году), ОЗО – общая заболеваемость по обращениям (число обращений населения в учреждения здравоохранения, приходящихся на 1000 человек населения), ОКС – общий коэффициент смертности (число умерших, приходящихся на 1000 человек населения), С – константа, позволяющая задавать среднее значение ИП для РФ в целом.

В приведённом выражении все ИП изменяются в интервале (0, 1), хотя это и не обязательно.

Факторный анализ на модели. Важной разновидностью исследуемых с помощью моделирования задач является факторный анализ. Его сущность заключается в исследовании влияния соответствующих параметров модели (факторов, входных факторов) на отклики (выходные факторы). В зависимости от числа анализируемых факторов различают однофакторный, двухфакторный, … , многофакторный анализ. При проведении факторного анализа изменяют только рассматриваемый входной фактор, а значения остальных факторов либо не меняются вообще, либо изменяются только от эксперимента к эксперименту. В последнем случае получают семейство таблиц, в каждой строке которых приводятся значения откликов, соответствующих выбранным значениям рассматриваемого фактора. Причем каждая такая таблица составляется для различных значений остальных факторов.

Отметим, что в последние годы исследование математических моделей чаще всего проводят в среде программирования Delphi (см. приложение П1), которая позволяет значительно облегчить работу программистов по разработке программы моделирования и упростить технологию моделирования. Поэтому все рассматриваемые в монографии программные решения задач математического моделирования приводятся для среды Delphi.

В литературе имеется достаточно много публикаций, посвящённых различным вопросам построения математических моделей и непосредственно моделированию. Большинство их осталось за пределами монографии [3, 8, 19, 20, 30, 33, 39, 43, 47, 50, 54, 59, 60, 63, 69, 75 и др.]. Монография в основном нацелена на реализацию и исследование математических моделей в среде программирования Delphi.

1) В таблице приведены результаты замеров отклика y от значений фактора x неизвестной структуры, на которую воздействуют помехи. Подобрать детерминированную модель зависимости y = f (x) и определить её параметры.

2) Моделями каких оригиналов являются глобус, журнал успеваемости преподавателя, изображение мамонта, нарисованное по его скелету, и выходные данные компьютерной программы Randomize?

3) Какие модели используются в методах Эйлера численного решения дифференциальных уравнений?

4) Привести примеры моделей в самолето- и в кораблестроении, в археологии и в милиции.

Рекомендация. Читателям, не знакомым со средой программирования Delphi, для понимания приводимых в монографии примеров программных решений рекомендуем ознакомиться с этой средой по приложению П1, которое автор старался изложить в простом, доступном широкому кругу читателей виде.