Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.1. Основные моделируемые структуры. Цифровые автоматы
В общем случае детерминированная техническая система, реализуемая с помощью работающих в дискретном времени t цифровых блоков (устройств), а также сами эти блоки можно представить в виде так называемых цифровых автоматов. Такой автомат имеет внутреннюю память, входную и выходную логические схемы (рис. 1.1). Согласно литературе цифровые автоматы делятся на автоматы Мура и автоматы Мили (по фамилиям соответствующих американских ученых – Moore machine и Mili machine). Аналоговые автоматы рассматриваться не будут (они в основном отжили).
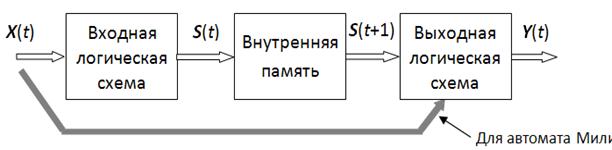
Рис. 1.1. Структурная схема цифровых автоматов Мура и Мили
Будем полагать, что входная и выходная логические схемы автоматов реализуют соответственно функции f и g, а содержимое внутренней памяти и ее входная величина подвергаются некоторому преобразованию h. Тогда поведение автомата Мура можем описать следующей системой уравнений, в которой в общем случае величины S, X и Y являются векторными:
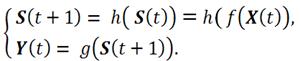
Для автомата Мили первое уравнение этой остаётся неизменным, а второе принимает следующий вид:
style=font-size:11.0pt;line-height:115%;font-family:"Calibri","sans-serif">
Приведенные выражения по существу задают разностные уравнения, реализуемые цифровыми автоматами. Такие уравнения можно рассматривать как модели соответствующих дифференциальных уравнений, описывающих процессы в реальном времени.
Отметим, что в автоматах Мили входной вектор style=font-size:14.0pt;font-family:"Calibri","sans-serif";position:relative; top:3.0pt>
можно подавать на выходную логическую схему и после прохождения им входной логической схемы. В этом случае