Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В СРЕДЕ DELPHI

Кирьянов Б Ф,

1.2. Математический аппарат, реализуемый в линейных детерминированных моделях, и основные задачи моделирования на их основе

Поскольку рассмотренные структуры цифровых автоматов являются обобщением большинства логических и арифметических устройств цифровой техники, то остановимся на вопросах их моделирования. Учтем, что обычно функции lang=EN-US>f, lang=EN-US>g и lang=EN-US>h являются линейными.

В указанном случае основным математическим аппаратом для построения моделей являются матричные (в частном случае – векторные) преобразования и линейные разностные уравнения. Рассмотрим их практическую реализацию.

Для выполнения матричных преобразований не требуются тактовые импульсы lang=EN-US>t (импульсы, реализующие временные шаги разностного уравнения, то есть шаги алгоритма). Рассмотрим на примере матричное преобразование входного вектора lang=EN-US>X, каждая координата которого задается некоторым числом. Пусть, например,

style=font-size:14.0pt;font-family:"Calibri","sans-serif">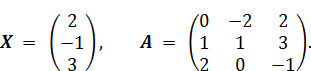

Тогда, изображаемое на схеме преобразование style=position:relative;top:9.0pt> при моделировании реализуется как style=font-size:14.0pt;font-family:"Calibri","sans-serif";position:relative; top:4.0pt> в случае представления вектора lang=EN-US>X вектором-столбцом или как style=font-size:14.0pt;font-family:"Calibri","sans-serif";position:relative; top:4.0pt> в случае представления этого вектора вектором-строкой. При этом результат lang=EN-US>Y lang=EN-US> получается на том же шаге, на котором появляется и lang=EN-US>X. Технически он реализуется с помощью логической схемы. В приведенном примере соответственно получаем:

style=font-size:14.0pt;font-family:"Calibri","sans-serif";position:relative; top:4.0pt> lang=EN-US>    или     style=font-size:14.0pt;font-family:"Calibri","sans-serif";position:relative; top:17.5pt>.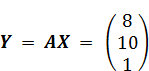

style=letter-spacing:-.2pt>При моделировании разностных уравнений соответствующие результаты должны получаться на разных шагах lang=EN-US style=letter-spacing:-.2pt>t style=letter-spacing:-.2pt>. style=letter-spacing:-.2pt> На схемах задержка на один шаг (такт) часто обозначается буквой lang=EN-US style=letter-spacing:-.2pt>D lang=EN-US style=letter-spacing:-.2pt> style=letter-spacing:-.2pt>( lang=EN-US style=letter-spacing:-.2pt>delay style=letter-spacing: -.2pt>). В программах задержка реализуется выбором соответствующей последовательности операторов программ.

Основная задача моделирования систем – исследование их поведения при различных значениях параметров. Центральной проблемой при этом является анализ устойчивости системы, описываемой разностными уравнениями, который в случае сложной правой части этих уравнений выполнить аналитически практически невозможно.

Известно несколько критериев устойчивости линейных цифровых систем, функционирование которых описывается системами разностных уравнений. Наибольшее применение получил, по-видимому, критерий устойчивости Ляпунова. Согласно ему решение системы уравнений размерности n называется устойчивым по Ляпунову, если для любого ненулевого конечного начального возмущения lang=EN-US>Y(0) существует такой вектор lang=EN-US>U lang=EN-US> размерности lang=EN-US>n lang=EN-US> lang=EN-US>c ограниченными координатами lang=EN-US>U _{lang=EN-US>i lang=EN-US>} > lang=EN-US> 0 style=position:relative;top:7.0pt> что при любом lang=EN-US>t lang=EN-US> > lang=EN-US> 0 для координат style=position:relative;top:6.0pt> «возмущённого» решения и координат lang=EN-US>Y_i( lang=EN-US>t) «невозмущённого» решений выполняется условие style=font-size:14.0pt;font-family:"Calibri","sans-serif";position:relative; top:3.0pt>( lang=EN-US>t) style=font-family:Symbol>½ style=font-family:Symbol>< style=font-size:14.0pt;font-family:"Calibri","sans-serif";position:relative; top:3.0pt> В противном случае решение называется неустойчивым. Устойчивое решение lang=EN-US>Y_i( lang=EN-US>t) называется асимптотически устойчивым, если вектор, координаты которого суть style=font-size:14.0pt;font-family:"Calibri","sans-serif";position:relative; top:3.0pt>( lang=EN-US>t) style=font-family:Symbol>½, style=position:relative;top:11.0pt> при неограниченном увеличении t стремится к нуль-вектору.

style=font-size:10.0pt>