Научная электронная библиотека

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В СРЕДЕ DELPHI

Кирьянов Б Ф,

1.3. Пример подготовки математического описания системы для её моделирования на компьютере

Пусть необходимо провести моделирование некоторой подсистемы, представляющей рассмотренный автомат Мура, в который добавлена обратная связь. Вариант схемы модели этого автомата приведён на рис. 1.2.

Так как матрица В не является нулевой, то схема на рис. 1.2 описывается неоднородным разностным уравнением:

style=font-size:14.0pt;font-family:"Calibri","sans-serif";position:relative; top:4.0pt>.

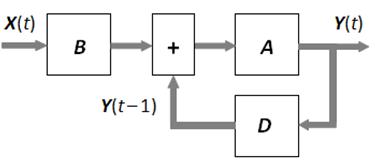
Рис. 1.2. Автомат Мура

Если матрица В – нулевая, что в технике эквивалентно отсутствию входных сигналов, то приведённая модель называется автономной.

Общее решение неоднородного уравнения состоит, как известно, из суммы решений однородной части U(t) = A Y(t–1) этого уравнения и частного решения указанного неоднородного уравнения. Необходимым условием устойчивости получаемого решения является устойчивость решения однородного уравнения. Для устойчивости решения однородного уравнения необходимо и достаточно, чтобы все характеристические числа λ_i этого уравнения (собственные значения матрицы A) находились в единичном круге комплексной плоскости. Если имеются ещё и некратные характеристические числа, лежащие на указанном круге, то решение считается условно устойчивым. Примером такого решения является дискретная синусоида с постоянной амплитудой колебаний.

Для трехмерной матрицы A значения её λ_i определяются из характеристического уравнения

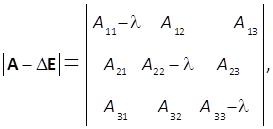
в котором E – единичная матрица.

Таким образом, если вопрос об устойчивости решения Y(t) рассматриваемого автомата можно решить на прибегая к моделированию, то графики этого векторного решения удобно получать с помощью моделирования.

Читателям рекомендуется составить векторное уравнение и соответствующую ему систему скалярных уравнений, описывающих работу автономной модели, приводимой на рис. 1.3. Матрицы A и B имеют размерность 3´3.

Y(t – 1)