Научная электронная библиотека

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

3.3. Некоторые обобщения задачи о кратчайшем пути

1⁰. Задача о кратчайших путях между всеми парами вершин состоит в одновременном определении длин между всеми парами вершин исходного графа. Существуют специализированные алгоритмы, которые гораздо быстрее решают эту задачу, чем простое применение обычных методов на хождения кратчайшего пути между парой вершин. Предложенные Флойдом (1962 г.) и Данцигом [52] (1966 г.) алгоритмы требуют сложений и сравнений, так что есть основания полагать их «неулучшаемыми».

2⁰. Задача о максимальном пути. Рассмотрим ориентированный граф с множеством вершин, перенумерованных индексом , у которого каждой дуге кроме длины приписано еще число , называемое пропускной способностью дуги, т.е. граф является 2-взвешенным. Содержательно означает максимальный объем груза, который можно в единицу времени перевезти по пути, обозначаемому дугой . Пусть некоторый путь от вершины к вершине и длина этого пути. Пропускной способностью этого пути является величина . Задача о максимальном пути заключается в отыскании такого пути , который максимизирует отношение . Содержательно эта математическая постановка представляет собой «задачу о пути с максимальной провозоспособностью». Путь , вообще говоря, является не единственным, т.е. этот путь можно представлять в виде переменной , , , в силу чего показатели и можно рассматривать как функции от и . Отсюда следует, что мы рассматриваем задачу дискретной оптимизации с дробной целевой функцией

(3.6)

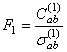Шаг 1. Используя алгоритм Дийкстры или другой метод, найдем в данном 2-взвешенном графе кратчайший путь от к . Пусть это будет путь длины . После этого находим пропускную способность и удаляем из графа все дуги с пропускной способностью и меньше. Полученный граф обозначим через , вычислим величину и перейдем к шагу 2.

Шаг . Пусть после - го шага получим граф и путь , которому соответствует величина . После этого удаляем из графа все дуги с пропускной способностью и меньше; получаем граф . Тогда в находим кратчайший путь длины , вычисляем его пропускную способность и находим величину , удаляем из все ребра с пропускной способностью и меньше. Полученный граф обозначаем через и переходим к шагу .

Алгоритм заканчивает свою работу, как только после очередного шага , перестанет существовать путь от вершины к вершине .

В результате работы алгоритма получим последовательность провозоспособностей , , среди которых находим максимальную. Пусть это будет . Тогда путь , полученный на -ом шаге и является искомым максимальным путем.

Нетрудно видеть, что число шагов строго меньше числа дуг в данном графе . С учетом установленной выше трудоёмкости алгоритма Дийкстры для -вершинного графа является очевидной оценка вычислительной сложности задачи о максимальном пути, которая ограничена сверху полиномом .

Примечание 3.2. Сформулированное выше примечание 3.1 является справедливым для задач с линейной целевой функцией вида (3.1). Однако, в задаче о максимальном пути с дробной целевой функцией (3.6) условия нечетких данных , порождают нетривиальную трудность инструментального характера. Эта трудность обусловлена тем, что к настоящему времени отсутствуют пригодные для целей оптимизации определения двух алгебраических действий: операция деления интервальных или нечетких чисел и операция сравнения и выбора (в смысле «лучше-хуже») интервальных или нечетких чисел. Таким образом, в условиях неопределенности данных для экстремальных задач на графах появляются алгоритмические проблемы, которые по своей степени сложности различаются следующим образом: по сравнению с линейной целевой функцией задача с дробной целевой функцией вида (3.6) оказывается принципиально более сложной.

3º. Задача о кратчайшем пути с линейным ограничением. Задается число и граф в котором каждой дуге кроме длины приписана также и стоимость . Задача состоит в отыскании такого пути из вершины в вершину , чтобы его длина была минимально возможной при выполнении ограничения . Для сформулированной таким образом постановки к настоящему времени достаточно эффективный метод решения неизвестен. Содержательно эту задачу можно трактовать как задачу выбора маршрута, обеспечивающего наименьшее возможное при ограниченных средствах время проезда из пункта в пункт .

Примечание 3.3. Задачу о кратчайшем пути с линейным ограничением можно рассматривать в роли конструктивного подхода к решению следующей 2-критериальной задачи. Пусть всякая дуга данного графа взвешена парой весов , . Качество решения оценивается 2-критериальной целевой функцией

(3.7)

где

, (3.8)

Векторная целевая функция определяет собой паретовское множество . Особо важным является тот факт, что определенный выше оптимум представляет собой паретовский оптимум . Этот факт позволяет использовать алгоритм линейной свертки критериев (3.8) для поиска, вообще говоря, приближенного решения задачи о кратчайшем пути с линейным ограничением. Суть этого метода состоит в том, что алгоритм Дийкстра последовательно применяется к данному графу , в котором его дуги последовательно по индексу взвешиваются сверткой весов , , , , , , . Тогда на выходе этого алгоритма получаем соответственно решения , которые представляют собой паретовские оптимумы [30], [74]. Они составляют подмножество , которое разбивается на две части и , где состоит из решений , удовлетворяющих условию задачи: . В качестве результата работы алгоритма из выбирается решение с минимальным значением критерия : . Остается открытым вопрос о достаточных условиях, при которых имеет место совпадение искомого и найденного .

4⁰. Обобщенная задача о кратчайшем пути. Пусть в графе его множество вершин разбито на подмножеств , . Требуется в найти кратчайший путь, исходящий из одной вершины множества , оканчивающийся в некоторой вершине множества и проходящий ровно одну вершину каждого множества , . Для этой задачи также не найдено достаточно эффективных методов решения. Отметим, что если в исходном разбиении , для каждого множества мощности , т.е. , то получим задачу о минимальном гамильтоновом пути.