Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

3.4. Задача о кратчайшем остовном дереве и ее приложения

Каждый связный граф содержит в качестве своего связного подграфа дерево с тем же количеством вершин, что и исходный граф, так называемое остовное дерево [45]. Задача состоит в том, чтобы для заданного неориентированного взвешенного графа  отыскать остовное дерево минимального веса или, что является синонимом, кратчайшего остовного дерева. При этом, наряду с термином «вес  ребра » используем его синоним «длина  ребра ».

Нам понадобится следующее

Определение 3.1. Фрагментом называется связный подграф остовного дерева графа . Вершину называем изолированным полюсом, если она не принадлежит никакому фрагменту.

Обоснование эффективного метода построения кратчайшего остовного дерева принадлежит Приму [77], [85]. Суть алгоритма Прима состоит в следующем. Как известно, в - вершинном графе его остовное дерево имеет  ребер. Алгоритм состоит из  шагов такого многошагового процесса, что на каждом очередном шаге к строящему (растущему) дереву присоединяется одно ребро. Прим сформулировал два основных принципа действия алгоритма на каждом шаге:

1) всякий изолированный полюс соединяется с ближайшей вершиной исходного графа;

2) всякий отдельный фрагмент соединяется с ближайшим соседом (полюсом или другим фрагментом) кратчайшим ребром.

Работа алгоритма начинается с выбора какого-нибудь полюса в качестве начального фрагмента и состоит в последовательном применении принципов 1) и 2) к имеющимся на данном шаге фрагментам или полюсам.

Пример 3.1. С помощью алгоритма Прима построим кратчайшее остовное дерево для 6-вершинного взвешенного графа, изображенного на рис.3.7.

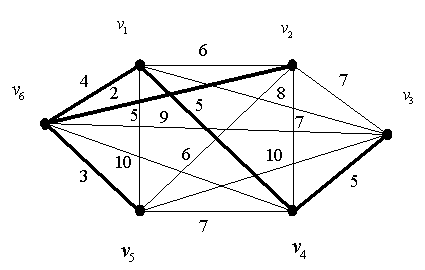
 Рисунок 3.7. Кратчайшее остовное дерево на 6-вершинном взвешенном графе

 Построение кратчайшего остовного дерева начнем с вершины . На первом шаге в качестве фрагмента  получим ребро . Ближайшим полюсом к  является вершина . В дальнейшем через  обозначим кратчайшее остовное дерево, выделяемое в  с помощью алгоритма Прима.

Обоснование алгоритма Прима вытекает из справедливости следующих двух необходимых условий для кратчайшего остовного дерева.

1⁰. Каждая вершина в кратчайшем остовном дереве  непосредственно связана по крайней мере с одной ближайшей вершиной.

2⁰. Каждый фрагмент в кратчайшем остовном дереве связан по крайней мере с одним ближайшим соседом (фрагментом) кратчайшим ребром.

Докажем справедливость условия 1⁰. Ради простоты будем предполагать, что все ребра  различны по длине . Из этого предположения вытекает

Следствие 3.1. Каждая вершина или каждый фрагмент в  имеет единственного ближайшего соседа.

Доказательство необходимых условий проведем рассуждением от противного. Предположим, что существует кратчайшее остовное дерево, для которого условие 1⁰ не выполнено. Тогда в нем найдется некоторая вершина , которая не соединена непосредственно со своим ближайшим соседом . Так как данное дерево есть связное дерево, то  обязательно соединена непосредственно с одной или несколькими вершинами отличными от , например, с . По той же самой причине вершина  соединена, через некоторую цепочку , с одной из вершин , например, с . Удалим теперь из данного кратчайшего остовного дерева ребро  и добавим ребро . Ясно, что связность вновь получившегося дерева не нарушится. В силу следствия 3.1 имеем строгое неравенство . Последнее означает, что мы получили более короткое остовное дерево, а это противоречит предположению, что в самом начале имели кратчайшее остовное дерево.

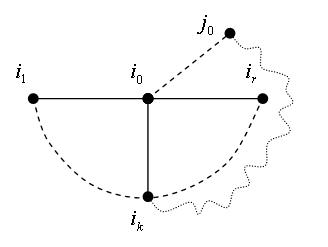
 Рисунок 3.8. Замена ребра () ребром .

 Необходимые условия 1⁰ и 2⁰ обосновывают принцип работы алгоритма Прима, согласно которому на каждом шаге  допускается добавление к фрагменту  только таких ребер, которые согласно 1⁰должны по необходимости войти в искомое кратчайшее остовное дерево.

Обращаясь теперь к обоснованию необходимости условия 2⁰, заметим, что приведенное выше доказательство необходимости условия 1⁰непосредственно переносится и на случай, если под  понимать не отдельный полюс, а фрагмент  такого кратчайшего остовного дерева, для которого по предположению не выполнено условие 2⁰. В этом случае ребро  является кратчайшим из ребер, которыми можно соединить фрагмент  с вершинами, принадлежащими фрагменту . Таким образом, мы осуществили обоснование необходимости условий 1⁰ и 2⁰.

Вернёмся к примеру 3.1. На втором шаге к фрагменту  присоединяем ребро , получим фрагмент . Ближайшим полюсом к фрагменту  является вершина . Поэтому результатом третьего шага является фрагмент . Продолжая аналогичным образом, получим на четвертом шаге  и на пятом шаге искомое кратчайшее остовное дерево . Трудоемкость алгоритма Прима имеет верхнюю оценку .

Примечание 3.4. Описанный выше метод применим для всяких весов , как положительных, так и отрицательных. Максимум множества действительных чисел равен по абсолютной величине, но противоположен по знаку минимуму множества этих чисел, взятых с противоположными знаками. Поэтому алгоритм Прима пригоден и для построения длиннейшего связывающего дерева. Для этого нужно только изменить знаки у весов  на противоположные. Более того, если веса , то кратчайшее остовное дерево минимизирует также произведение  и корень квадратный из суммы квадратов . В то же время кратчайшее остовное дерево  максимизирует сумму обратных дробей  и произведение арккотангенсов .

Сформулируем несколько обобщений задачи о кратчайшем остовном дереве, которые важны в прикладном отношении, но эффективных методов решения не имеют.