Научная электронная библиотека

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

3.6. Эйлеровы обходы (маршруты) в графах.

3.6.1. Задача об эйлеровом обходе формулируется следующим образом. Пусть задан связной неориентированный граф . Спрашивается, можно ли найти в такой цикл , который содержит все вершины и все ребра исходного графа, при условии, что в маршруте, задаваемом циклом , каждое ребро встречается один и только один раз?


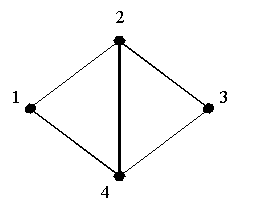
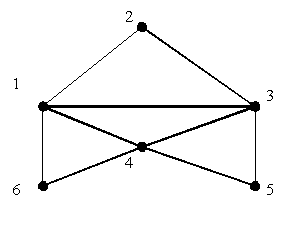
Рисунок 3.14. Неэйлеров граф	Рисунок 3.15. Эйлеров граф

Такой цикл , удовлетворяющий сформулированному определению, если он существует, называется Эйлеровым циклом, а граф , содержащий , называется Эйлеровым графом.

На рис.3.14 изображен граф, не являющийся Эйлеровым. Граф, изображенный на рис.3.15, является Эйлеровым, т.к. он содержит Эйлеров цикл .

В 1736 году Эйлером была доказано утверждение следующего содержания.

Теорема 3.5. Граф является Эйлеровым тогда и только тогда, когда он связен и степени всех его вершин четны.

Толчком к доказательству этой первой в теории графов теоремы послужила широко известная в то время задача, называвшаяся проблемой кёнигсбергских мостов (см., например [50]). Можно сказать, что исторически теория графов, как наука, началась с этой теоремы, а Л. Эйлер является отцом теории графов.

Сформулированная в настоящем параграфе задача решена в том смысле, что уже построены вполне эффективные алгоритмы для непосредственного выявления Эйлерова цикла. Укажем, например алгоритм Флёри (Fleury) [50], или алгоритм Хоанг Туи [35]. Суть алгоритма Флёри в том, что для выделения Эйлерова цикла в G достаточно придерживаться следующих правил:

1⁰. Выходим из произвольной вершины данного графа ; каждое пройденное ребро зачеркиваем.

2⁰. Никогда не идем по такому ребру , которое в рассматриваемый момент является перешейком, т.е. при удалении которого граф, образованный незачеркнутыми ребрами, распадается на две компоненты связности, имеющие хотя бы по одному ребру.

Осуществляя конструктивное доказательство теоремы 3.5, мы тем самым достаточно подробно изложим работу еще одного алгоритма выделения Эйлерова цикла в .

Доказательство теоремы 3.5.

Необходимость. Необходимость связности графа , если в нем имеется Эйлеров цикл, очевидна. Необходимость четности степеней всех вершин в следует из того, что при Эйлеровом обходе нужно входить в каждую вершину и выходить из нее одно и то же число раз, . Следовательно степень каждой вершины равна четному числу .

Достаточность. Предположим, что граф связен и степени всех его вершин четны. Начиная с вершины , будем строить цепь по принципу: «на каждом шаге построения проходим по ребру, ещё не пройдённому ранее». Так как по условию в каждой вершине сходится четное число рёбер, то при движении по маршруту из каждой вершины будет возможен выход, т.е. на каждом шаге, попав в вершину , будем иметь в своём распоряжении ещё не пройденное ранее ребро, по которому можем продолжать построение цепи . В виду конечности множества этот процесс должен заканчиваться тем, что мы попадём в исходную вершину и таким образом цепь замкнётся в цикл .

Если проходит через все ребра , то мы уже получили искомый Эйлеров цикл . Пусть не все ребра из попали в . Тогда в силу связности графа найдется вершина , принадлежащая , и инцидентная некоторому ребру , которая не принадлежит .

Например, пусть в графе, изображенном на рис.3.15 в качестве исходной вершины мы взяли и построили цикл . Тогда в качестве можно взять вершину 1, которой инцидентно ребро .

Теперь, начиная с вершины , будем строить новую цепь , используя на этот раз только те ребра, которые не принадлежат . Так как по условию вершина инцидентна четному числу ребер, то число ребер, инцидентных и не принадлежащих , также четно. Это утверждение справедливо и для всех других вершин, через которые будет проходить строящаяся цепь . Поэтому, как и для , цепь в исходной вершине замкнется в цикл .

Объединяя циклы и , получим цикл . Если включает в себя все ребра , то он является искомым Эйлеровым циклом . В противном случае найдется вершина , принадлежащая и инцидентная некоторому ребру (), которое не принадлежит циклу . Начиная с вершины строим новый цикл , используя только те ребра, которые не принадлежат . Объединяя и , получим цикл , в отношении которого проводим те же рассуждения, что и для .

Продолжая описанный выше процесс построения циклов , , через конечное число шагов получим цикл , который включает в себя все ребра исходного графа . Цикл по определению и есть искомый Эйлеровый цикл.

Теорема 3.5 доказана полностью. Заметим, что эта теорема справедлива также и для случая, когда – это мультиграф.

В отношении ориентированных графов и мультиграфов также справедливо следующее аналогичное утверждение.

Теорема 3.6 [35]. Пусть – конечный ориентированный связный граф с множеством дуг . Для того, чтобы существовал (ориентированный) контур, содержащий все дуги из , необходимо и достаточно, чтобы в каждой вершине число входящих и выходящих дуг было одинаковым.

3.6.2. Рассмотрим теперь более общую задачу построения аппроксимирующего Эйлерова цикла, оптимального относительно некоторого критерия. Эта задача означает нахождение минимального Эйлерова мультиграфа для связного графа со взвешенными ребрами и формулируется следующим образом. Задан - вершинный неориентированный связный граф , у которого каждому ребру приписано число . Задача состоит в том, чтобы указать такой замкнутый маршрут обхода всех ребер графа , при котором его длина минимальна (здесь суммирование ведется с учетом кратности прохождения маршрута через каждое ребро ).

Например, пусть – это граф, изображенный на рис.3.14, в котором ребру приписан вес 5, остальным ребрам приписан вес, равный 1. Тогда одним из кратчайших обходов всех ребер этого графа является маршрут . Если в этом решении каждое ребро продублировать столько раз, сколько раз оно встречается в , то получим Эйлеров мультиграф , изображенный на рис.3.16. Исходный граф является частичным графом для этого мультиграфа.

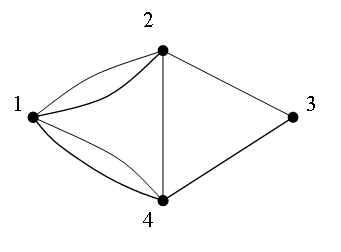
Рисунок 3.16. Эйлеров мультиграф для графа на рис. 3.14

Как мы установили ранее, для Эйлерова мультиграфа выделение Эйлерова цикла не представляет особого труда. Поэтому принято считать, что нахождение кратчайшего маршрута для и построение аппроксимирующего мультиграфа , множество ребер которого включает , и сумма весов ребер которого минимальна – это одна и та же задача.

Кратко эти задачи называют “задачей обходчика”. Последнее название возникло из изучения следующей ситуации. Имеется разветвленная сеть дорог, например, железнодорожных путей. Перед обходчиком стоит задача обойти все участки этой транспортной сети за минимальное время, т.е. так, чтобы общий пройденный путь имел минимальную длину. Другое название этой задачи «Китайский почтальон». Полиномиальный алгоритм этой задачи базируется на следующем утверждении.

Теорема 3.7. Для всякого графа со взвешенными ребрами искомый минимальный Эйлеров мультиграф таков, что его можно разложить на два обыкновенных графа и таких, что , – частичный подграф графа . При этом нахождение подграфа сводится к решению задачи об оптимальном совершенном паросочетании на полном взвешенном графе, размерность которого равна количеству вершин нечеткой степени в .