
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
МЕТОДЫ ФОТОМЕТРИЧЕСКОГО АНАЛИЗА В САНИТАРНО-ГИГИЕНИЧЕСКИХ ИССЛЕДОВАНИЯХ
Дорогова В Б, Игнатьева Л П,
4.2. Расчет основных метрологических характеристик результатов прямых (непосредственных) равноточных измерений
В химическом анализе содержание вещества в пробе устанавливают, как правило, по небольшому числу параллельных определений (п ? 3). Для расчета погрешностей определений в этом случае пользуются методами математической статистики, разработанными для малого числа определений. Полученные результаты рассматривают как случайную (малую) выборку из некоторой гипотетической генеральной совокупности, состоящей из всех мыслимых в данных условиях наблюдений. Соответственно различают выборочные параметры (параметры малой выборки) случайной величины, которые зависят от числа наблюдений, и параметры генеральной совокупности, не зависящие от числа наблюдений. Для практических целей можно считать, что при числе измерений п = 20–30 значения стандартного отклонения генеральной совокупности (s) – основного параметра – и стандартного отклонения малой выборки (s) близки (s ? s).
Все измерения в метрологии делят на прямые и косвенные. При прямых непосредственных измерениях числовое значение измеряемой величины х сразу получается из показаний прибора, при помощи которого выполняется данное измерение, например значение оптической плотности или пропускания при отсчете по шкале оптической плотности (пропускания) спектрофотометра или фотоколориметра. Результат каждого прямого измерения включает случайную погрешность, которая зависит от большого числа случайных факторов. Если отклонения, вызванные случайными факторами, сравнимы по абсолютному значению с чувствительностью прибора, то они обнаруживаются приборами, и при п измерениях одной и той же величины получаются результаты х1, х2, хi, хп, которые могут отличаться друг от друга в пределах чувствительности данных измерений.
Статистическую обработку результатов измерений малой выборки (п), оценку их воспроизводимости и правильности осуществляют по нижеприведенной схеме.
Предполагается, что выборка имеет приближенно нормальный закон распределения. Отклонения от гауссовского распределения могут иметь место, особенно при определении следовых содержаний компонентов. При этом возможно логарифмическое нормальное распределение. При необходимости следует осуществить проверку нормальности распределения.
Среднее выборки. Пусть х1, х2, ...., хп обозначают п результатов измерений величины, истинное значение которой ?. Предполагается, что все измерения проделаны одним методом и с одинаковой тщательностью. Такие измерения называют равноточными.
В теории ошибок доказывается, что при условии выполнения нормального закона (закона распределения Гаусса) при п измерениях одинаковой точности среднее арифметическое из результатов, полученных при всех измерениях, является наиболее вероятным и наилучшим значением измеряемой величины:
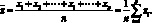 (4.4)
(4.4)
Это среднее значение принимают за приближенное и пишут 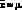
Единичное отклонение – отклонение отдельного измерения от среднего арифметического:
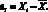 (4.5)
(4.5)
Алгебраическая сумма единичных отклонений равна нулю
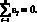
Дисперсия, стандартное отклонение, относительное стандартное отклонение. Рассеяние результатов измерений относительно среднего значения принято характеризовать дисперсией s2:
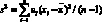 (4.6)
(4.6)
или стандартным отклонением (средним квадратическим отклонением – СКО) – s:
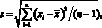 (4.7)
(4.7)
которое обычно и приводят при представлении результатов измерений (анализа) и которым характеризуют их прецизионность.
Стандартное отклонение, деленное на среднее выборки, называют относительным стандартным отклонением:
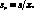 (4.8)
(4.8)
В общем случае метод (методика) анализа оптимален в той области содержаний, в которой и абсолютное (s), и относительное (Sr) стандартные отклонения имеют минимальные значения.
Дисперсия среднего арифметического (выборки), стандартное отклонение среднего арифметического (выборки). При оценке воспроизводимости полученных результатов вычисляют также дисперсию среднего арифметического:
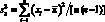 (4.9)
(4.9)
и стандартное отклонение среднего арифметического:
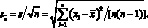 (4.10)
(4.10)