Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Дискретная оптимизация и моделирование в условиях неопределенности данных
Перепелица В. А., Тебуева Ф. Б.,
3.7.2. Решение задачи коммивояжера методом динамического программирования
В основе метода динамического программирования лежит простая идея осуществления сравнения различных вариантов допустимых решений задачи (по значению целевой функции) не в конце построения множества всех возможных вариантов, а на каждом шаге построения возможных вариантов [16], [35]. Применительно к задаче коммивояжера содержание работы алгоритма на 
-ом шаге, 
состоит в том, что имеющиеся пути коммивояжера “длины ” (т.е. проходящие через вершин) удлиняем на единицу, т.е. получаем пути, проходящие через 
вершин.
Пусть нам задан 
-вершинный граф 
, в котором вершины перенумерованы индексом 
; 
, 
, 
– матрица длин, т.е. весов 
дуг 
. Так как искомый гамильтонов контур есть замкнутый путь, то, не умаляя общности, можно считать, что начальной является вершина 0.
Пусть дан оптимальный путь коммивояжера 
. Рассмотрим в 
отрезок пути, начинающийся в 0 и заканчивающийся вершиной 
: 
; этот путь содержит промежуточных вершин. Очевидно, что так как – минимальный гамильтонов контур, то его часть 
, соединяющая вершины 0 и 
и проходящая в некотором порядке через вершины 
должна иметь минимальную длину. Введем обозначение
(3.29)
– длина пути минимальной длины, соединяющего вершины 0 и и проходящего один и только один раз через каждую из вершин 
.
В обозначениях (3.29) общий принцип оптимальности в теории динамического программирования [16] применительно к задаче коммивояжера имеет следующий вид:
(3.30)
Здесь уместно напомнить, что функция (3.29) симметрична по аргументам 
, т.е. не изменяется при любой их перестановке.
Перейдем непосредственно к изложению алгоритма.
Шаг 0. Вычисляем функцию
, 
, если дуга 
,(3.31)
Æ – пустое множество. Запоминаем все 
значений этой функции.
Шаг 1. Вычисляем функцию
(3.32)
, 
.
Запоминаем все 
значений функции (3.32), после чего вычеркиваем из памяти таблицу значений функции (3.31).
Шаг (
). Для всех 
и всех 
наборов 
вычисляем функцию 
по формуле (3.30). При этом всякий раз функция (3.30) вычисляется только для таких наборов, что 
. Для каждого значения функции (3.30) наряду с ним запоминаем оптимальную перестановку элементов , на которой реализуется фигурирующий в определении (3.29) путь 
. По окончанию вычислений вычеркиваем из памяти полученную на предыдущем шаге 
таблицу значений 
, а также соответствующие каждой функции оптимальные пути.
Подсчитаем трудоемкость алгоритма динамического программирования на - ом шаге. Количество значений 
функции 
, подлежащих вычислению и запоминанию, равно
(3.33)
На одно значение функции требуется 
действий (
выборов из таблицы, 
сложений, 
сравнений). Необходимый объем памяти 
(до вычеркивания из памяти таблиц и соответствующих оптимальных перестановок из элементов 
)) составляет
(3.34)
Шаг . Имея таблицу значений функций 
и список соответствующих им оптимальных перестановок из элементов 
, вычисляем функцию
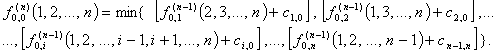
Перестановка, на которой достигается этот минимум, однозначно определит искомый оптимум задачи коммивояжера.
Просуммировав величины (3.33) по шагам 
, получим выражение для суммарного объема 
необходимых вычислений: 
операций. Аналогично согласно (3.34) получим, что для решения задачи коммивояжера с помощью алгоритма динамического программирования требуется память 
ячеек.
Нетрудно убедиться, что реализация этого алгоритма на современных ПЭВМ ограничивается как по оперативной памяти, так и по быстродействию (продолжительности процесса счета) значениями 
порядка 50.