
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ФИНАНСОВЫЙ АНАЛИЗ: РИСКИ, КРЕДИТОСПОСОБНОСТЬ, ИНВЕСТИЦИИ
Бороухин Д. С., Царева С. В., Гапоненкова Н. Б., Мотина Т. Н., Бреславец И. Н., Беспалова С. В., Дрождинина А. И., Скотаренко О. В., Смирнов А. В., Рапницкая Н. М., Кибиткин А. И.,
1.3. Показатели оценки предпринимательских и финансовых рисков
В данном параграфе мы рассмотрим основные показатели, с помощью которых производится оценка предпринимательских и финансовых рисков.
Для расчета приведенных в данном параграфе мер риска необходимо наличие достаточного объема выборки значений исследуемых показателей (прибыли/убытки, доходности и т.д.). Это является существенным ограничением для оценки большинства рисков, по которым невозможно в силу объективных причин получить достаточную по объему выборку анализируемых показателей.
Одним из наиболее широко используемых показателей риска является дисперсия (variance). Риск в контексте данного показателя представляет собой степень изменчивости экономических или финансовых переменных, которые по своей природе являются случайными величинами. Несмещенная оценка выборочной дисперсии случайной величины X производится по следующей формуле:
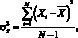 (1.1)
(1.1)
|
где |
дисперсия случайной величины X; |
|
Xi – |
значение случайной величины X в момент времени i; |
|
|
среднее значение случайной величины X; |
|
N – |
объем выборки. |
Среднее значение определяется как среднее арифметическое значений случайной величины и определяется по следующей формуле:
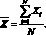 (1.2)
(1.2)
Дисперсия измеряется как квадрат единицы измерения случайной величины. Например, дисперсия квартальной прибыли измеряется в рублях в квадрате, дисперсия доходности финансовых активов измеряется в%. Более удобным, с точки зрения применения на практике, является показатель среднеквадратического отклонения или стандартной ошибки (standard deviation, standard error), который рассчитывается по следующей формуле:
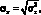 (1.3)
(1.3)
где ?x – среднеквадратическое отклонение случайной величины X.
Среднеквадратическое отклонение измеряется в тех же самых единицах измерения, что и сама случайная величина.
Рассмотрим пример (1.1). В таблице, представленной ниже, даны сведения о размере прибыли рыбной отрасли региона за 10 последовательных кварталов.
Таблица 1.2
Сведения о размере прибыли
|
Квартал |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Прибыль, руб. |
10 |
0 |
4 |
–4 |
5 |
15 |
20 |
30 |
20 |
0 |
Найдем среднее значение и стандартное отклонение квартальной прибыли. Среднее значение находим по формуле (1.2). Среднее арифметическое квартальных прибылей равно 10 руб. Среднеквадратическое отклонение определяем как квадратный корень из дисперсии. Дисперсию квартальных прибылей рассчитываем по формуле (1.1).
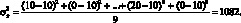
Квадратный корень из дисперсии равен 10,96. Таким образом, квартальная прибыль компании имеет среднее значение 10 руб. и стандартное отклонение 10,96 руб.
Как видно из приведенных формул и дисперсия и стандартное отклонение представляют собой меры разброса случайной величины вокруг своего среднего значения. Показатели учитывают как негативные, так и положительные отклонения от ожидаемого результата, что с точки зрения управления риском не всегда бывает удобным, поскольку, например, лицу, принимающему решение в условиях риска, более важны негативные отклонения и убытки, чем положительные отклонения и прибыли. Для учета только отрицательных исходов в практике риск-менеджмента помимо показателя стандартного отклонения также используют показатель полустандартного отклонения (semistandard deviation), являющегося аналогом стандартного отклонения и учитывающего только убыточные результаты. Полустандартное отклонение рассчитывается по формуле:
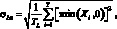 (1.4)
(1.4)
|
где ?Lx – |
полустандартное отклонение; |
|
TL – |
количество убыточных исходов; |
|
Min() – |
оператор нахождения минимального из двух величин, находящихся в скобках и разделенных запятой. |
На практике знание только стандартного отклонения бывает недостаточно для того, чтобы принять решение в ситуации выбора из нескольких альтернатив. Одним из полезных показателей, позволяющим сравнить колеблемость определенного параметра в нескольких совокупностях с различными средними значениями (например, оценить разброс значений прибыли среди нескольких альтернативных проектов с различными показателями стандартных отклонений и средних значений прибыли) является коэффициент вариации. Данный коэффициент определяется по формуле:
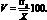 (1.5)
(1.5)
Коэффициент вариации измеряется в процентах, является мерой относительного разброса и показывает, какую долю среднего значения параметра составляет его средний разброс. Чем выше показатель вариации, тем больше риск. Продолжим рассмотрение примера (1.1) и добавим данные по квартальной прибыли для второй компании (см. табл. 1.3)
Таблица 1.3
Сведения о размере прибыли
|
Квартал |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Прибыль, руб. |
5 |
–5 |
–1 |
–9 |
0 |
10 |
15 |
25 |
15 |
–5 |
Как нетрудно убедиться среднее значение квартальной прибыли составляет 5 руб., а среднеквадратическое отклонение, как и в случае с первой компанией, составляет 10,96 руб. В первом и во втором случае прибыли компаний имеют одинаковый разброс, но среднее значение прибыли в первом случае больше, и соответственно больше коэффициент вариации – 109,65 % для первой компании против 219,3 % для второй компании.
С помощью дисперсии и стандартного отклонения измеряют риск не только отдельных активов, но и портфелей активов. При рассмотрении риска на уровне портфеля активов на первый план выходят вопросы оценки взаимосвязей между активами, составляющими портфель. Одним из наиболее важных показателей в риск-менеджменте, оценивающим тесноту связи между случайными величинами, является коэффициент ковариации, а также нормированный коэффициент ковариации – коэффициент корреляции. Приведем формулы для расчета данных коэффициентов для двух случайных величин X и Y на основе выборочных данных:
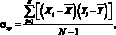 (1.6)
(1.6)
|
где ?xy – |
ковариация случайных величин X и Y; |
|
Xi, Yi – |
значения случайных величин X и Y в момент времени i; |
|
|
среднее значение случайных величин X и Y соответственно. |
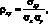 (1.7)
(1.7)
|
где ?xy – |
корреляция случайных величин X и Y; |
|
?x, ?y, – |
среднеквадратические отклонения случайных величин X и Y соответственно. |
Коэффициент корреляции измеряет степень линейной связи (неприменим в случае наличия нелинейных взаимосвязей) и является безразмерным показателем, который изменяется в пределах от –1 до + 1 включительно. Если коэффициент корреляции равен –1 или + 1, то это говорит о наличии абсолютной отрицательной или положительной линейной взаимосвязи между величинами. Если коэффициент корреляции равен или близок к нулю, то это говорит об отсутствии значимой линейной связи между величинами (значимость коэффициента корреляции оценивается с помощью специальных статистических тестов).
Рассмотрим следующий пример (1.2). Определим ковариацию и корреляцию доходностей двух финансовых активов рыболовецкой фирмы, например двух ценных бумаг А и Б. В табл. 1.4 представлена информация о значениях доходностей ценных бумаг А и Б за 10 последовательных
периодов.
Таблица 1.4
Доходность ценных бумаг А и Б
|
Период |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Доходность ценной бумаги А, % |
10 |
5 |
–15 |
0 |
7 |
–5 |
15 |
10 |
0 |
3 |
|
Доходность ценной бумаги Б, % |
–4 |
–10 |
5 |
0 |
10 |
15 |
8 |
–10 |
–5 |
3 |
Средние значения доходностей найдем по формуле (1.2). Для ценных бумаг А и Б средние доходности равны 3 и 12 % соответственно. Далее по формуле (1.6) найдем ковариацию доходностей ценных бумаг А и Б:
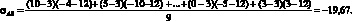
Ковариация доходностей измеряется в процентах в квадрате (аналогично дисперсии).
Для расчета коэффициента корреляции доходностей предварительно найдем среднеквадратические отклонения доходностей с использованием формул (1.1) и (1.3). Среднеквадратические отклонения доходностей для ценных бумаг А и Б равны 8,62 и 14,2 % соответственно. Далее воспользуемся формулой (1.6) для расчета коэффициента корреляции доходностей ценных бумаг А и Б:
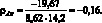
Значение коэффициента корреляции –0,16 говорит о небольшой отрицательной взаимосвязи между доходностями ценных бумаг.
Дисперсия доходности портфеля активов определяется по следующей формуле:
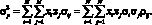 (1.8)
(1.8)
Дисперсия доходности портфеля также может быть записана в следующем виде:
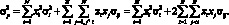 (1.9)
(1.9)
В матричном виде дисперсия портфеля записывается в более компактной форме:
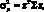 (1.10)
(1.10)
|
где x – |
вектор-столбец весов активов; |
|
? – |
ковариационная матрица. |
Ковариационная матрица является квадратной матрицей, каждый элемент которой (за исключением элементов, располагающихся на главной диагонали) представляет собой коэффициент ковариации ?ij соответствующих активов i и j. Ниже представлена ковариационная матрица ? для двух активов:
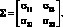
Элементы ковариационной матрицы, располагающиеся на главной диагонали (?11 и ?22 для случая двух активов), представляют собой дисперсии доходностей первого и второго актива соответственно. Недиагональные элементы матрицы являются коэффициентами ковариации первого и второго актива. При этом необходимо отметить, что равен(в этом нетрудно убедиться, если обратиться к формуле расчета коэффициента ковариации). Исходя из этого, ковариационная матрица является симметричной относительной главной диагонали и для того, чтобы задать всю ковариационную матрицу, нет необходимости рассчитывать все парные ковариации.
Рассмотрим пример (1.3) расчета риска портфеля, состоящего из двух активов. При этом воспользуемся операциями с матрицами для расчета стандартного отклонения доходности портфеля. Дан вектор-столбец весов активов в портфеле:
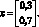
Задана ковариационная матрица доходностей активов:
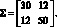
Используя формулу (1.10) найдем дисперсию доходности портфеля:
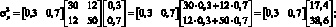
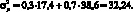
По формуле (1.3) стандартное отклонение доходности портфеля равно 5,68 %. Значение стандартного отклонения доходности всего портфеля близко к значению стандартного отклонения первого актива (5,48 %), при этом значительно меньше стандартного отклонения доходности второго актива (7,07 %). Как будет показано ниже, риск портфеля можно сделать меньше, чем риск составляющих его активов, за счет эффекта диверсификации портфеля.
Для случая двух активов дисперсия доходности портфеля будет равна:
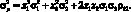 (1.11)
(1.11)
Поставим задачу нахождения портфеля (т.е. определение его структуры) состоящего из двух активов и имеющего минимальный риск. С учетом того, что сумма долей активов в портфеле равна 1, то x2 = 1 – x1. С учетом этого дисперсия портфеля равна:
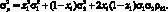 (1.12)
(1.12)
Вычислим производную по параметру x1:
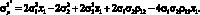 (1.13)
(1.13)
Приравняем производную к нулю и решим уравнение относительно x1:
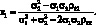 (1.14)
(1.14)
Рассмотрим некоторые частные случаи.
1. Если доходности активов связаны абсолютной положительной связью (?12 = 1), то доли активов будут равны:
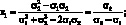 (1.15)
(1.15)
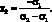 (1.16)
(1.16)
Как нетрудно убедиться в этом случае дисперсия доходности портфеля будет равна нулю. Особенность такого портфеля заключается в том, что в отношении второго актива совершается операция «короткая» продажа (short sale), это видно из того, что его доля отрицательна, при этом весь капитал инвестируется в первый активов. Только при такой стратегии достигается минимальный риск.
2. Если доходности активов являются независимыми величинами (?12 = 0), то доли активов равны:
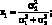 (1.17)
(1.17)
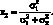 (1.18)
(1.18)
Дисперсия портфеля в этом случае будет равна:
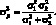 (1.19)
(1.19)
3. Если доходности активов отрицательно коррелированны (?12 = –1), то доли активов определяются как:
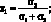 (1.20)
(1.20)
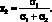 (1.21)
(1.21)
Дисперсия доходности данного портфеля, как и в первом случае, будет равна нулю. Только здесь это является следствием абсолютной отрицательной корреляции доходностей активов, когда рост или падение доходности одного актива полностью компенсируется падением или ростом доходности другого актива.
Рассмотрим следующий пример (1.4). Пусть даны две ценные бумаги А и Б, имеющие стандартное отклонение доходности 7 и 13 % соответственно. В первом случае предположим, что корреляция доходностей активов составляет –1, во втором случае 0, в третьем случае +1. Найдем риск портфеля для каждого варианта при условии, что доли ценных бумаг А и Б в портфеле составляют 0,7 и 0,3 соответственно. Для расчета риска будем использовать формулу (1.8). Дисперсия доходности портфеля для первого варианта равна:
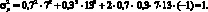
Аналогичный расчет для второго и третьего варианта дает результаты 39,22 и 77,44 соответственно. Стандартные отклонения доходности портфеля для первого, второго и третьего варианта равны 1; 6,26 и 8,8 % соответственно. Как видно из полученных результатов наименьший риск соответствует случаю абсолютной отрицательной корреляции доходностей. Риск портфеля ниже, чем риск каждого отдельно взятого актива.
Проиллюстрируем влияние на общий риск портфеля изменений весов активов при 3 вариантах корреляции доходностей и при отсутствии операции «короткая» продажа. Рассмотрим, как изменится стандартное отклонение доходности портфеля при уменьшении доли ценной бумаги Б с 1 до 0 при соответствующем росте доли ценной бумаги А с 0 до 1. Как видно из рис. 1.8–1.10 в крайних случаях, когда портфель включает только ценную бумагу А или ценную бумагу Б, стандартное отклонение портфеля соответствует стандартному отклонению доходности ценной бумаги А или Б. Однако, при изменении долей ценных бумаг в портфеле стандартное отклонение портфеля ведет себя по-разному в зависимости от степени корреляции доходностей активов. В случае, когда корреляция доходностей активов равна 1, то не происходит уменьшения риска портфеля, а наблюдается лишь усреднение рисков отдельных ценных бумаг, эффекта диверсификации не наступает. Однако, если доходности активов отрицательно коррелированны (см. рис. 1.7), то наблюдается эффект диверсификации, когда риск портфеля значительно меньше, чем риск составляющих его активов.
Продолжим далее исследовать зависимости. Рассмотрим следующий пример (1.5). Дан портфель, состоящий из двух ценных бумаг А и Б, с весами 0,3 и 0,7 соответственно. Стандартное отклонение доходности ценной бумаги А равно 10 %, а ценной бумаги Б – 15 %. Посмотрим, какое влияние на общий риск портфеля окажет изменение корреляции доходностей ценных бумаг А и Б от –1 до 1. Как видно из рис. (1.10) стандартное отклонение доходности портфеля монотонно возрастает по мере увеличения корреляции между ценными бумагами. Это подтверждает предыдущие выводы о том, что чем более отрицательно коррелированны доходности активов в портфеле, тем меньше волатильность доходности портфеля в целом и меньше его риск. Таким образом, достижение эффекта диверсификации возможно за счет включения в портфель активов, доходности которых являются максимально отрицательно коррелированными.
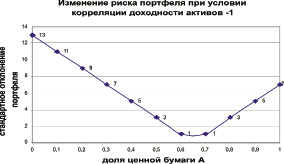
Рис. 1.7. Стандартное отклонение доходности портфеля, состоящего из двух активов, имеющих корреляцию доходностей –1
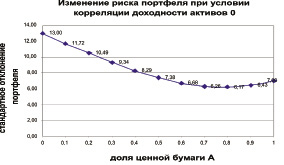
Рис. 1.8. Стандартное отклонение доходности портфеля, состоящего из двух активов, имеющих корреляцию доходностей 0
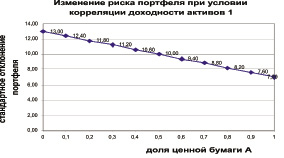
Рис. 1.9. Стандартное отклонение доходности портфеля, состоящего из двух активов, имеющих корреляцию доходностей + 1
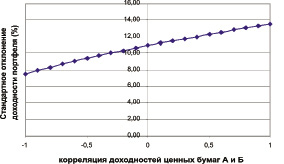
Рис. 1.10. Влияние изменения корреляции доходностей
активов на общий риск портфеля
Это является одним из основных выводов, сделанных нобелевским лауреатом по экономике Г. Марковицем.
Как было показано выше, для того чтобы оценить риск всего портфеля активов необходимо оценить все парные ковариации всех активов портфеля. В случае оценки риска хорошо диверсифицированного портфеля это потребует значительного объема вычислений. Так, для портфеля, состоящего из 10 активов, для оценки всей ковариационной матрицы необходимо произвести 55 вычислений, а для портфеля, состоящего из 100 активов, это уже 5050 вычислений. Очевидно, что портфель, включающий сотни и тысячи активов, потребует значительного объема вычислений. Данную проблему решает предложенная модель САРМ (capital assets pricing model), одним из авторов которой является нобелевский лауреат по экономике, профессор Стэндфорского университета У.Шарп. Более подробно с данной моделью можно ознакомиться в специализированной литературе. Здесь же мы остановимся на некоторых аспектах данной модели, а также рыночной модели, также предложенной У. Шарпом (САРМ является моделью равновесного рынка, рыночная модель не является равновесной моделью и не требует дополнительных условий). Во-первых, была предложена мера риска – коэффициент бета, которая оценивает чувствительность доходности актива по отношению к рыночному портфелю (модель САРМ) или некоторому индексу (рыночная модель) и является мерой т.н. систематического или рыночного риска. Во-вторых, была предложена идея разделения общего риска актива и риска всего портфеля на две составляющие: первая составляющая связана с рыночном риском (систематический риск), вторая – с индивидуальным риском каждого актива (несистематический риск).
Коэффициент бета или просто бета является достаточно популярным показателем, который публикуют некоторые финансовые издания наравне с котировками финансовых активов. Бета актива ?i рассчитывается по следующей формуле:
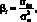 (1.22)
(1.22)
|
где ?im – |
ковариация доходности актива i и рыночного портфеля; |
|
|
дисперсия доходности рыночного портфеля. |
Бета измеряет чувствительность доходности актива по отношению к изменению доходности рыночного портфеля (или индекса). Если бета > 1, то доходность актива изменяется сильнее, чем доходность рыночного портфеля (или индекса), и такой актив считается более рисковым относительно рынка в целом. Если бета < 1, то доходность актива изменяется меньше, чем доходность рыночного портфеля (или индекса), и такой актив является менее рисковым. Бета рыночного портфеля равна 1. С точки зрения теории, рыночный портфель включает в себя все рисковые активы, обращающиеся на рынке. На практике при оценке доходности акций на основе модели САРМ используют подход на основе широкого фондового индекса. С точки зрения статистики коэффициент бета актива представляет собой коэффициент наклона простой линейной регрессии. На практике его оценивают на основе выборки.
Рассмотрим следующий пример (1.6). В табл. 1.5, приведенной ниже, даны сведения о доходности индекса и ценной бумаги А за 10 последовательных периодов. Необходимо определить коэффициент бета ценной бумаги А.
Таблица 1.5
Данные о значениях доходности индекса и ценной бумаги
|
Период |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Доходность |
5 |
3 |
7 |
–4 |
–46 |
0 |
2 |
6 |
4 |
3 |
|
Доходность ценной бумаги А, % |
–42 |
0 |
5 |
3 |
–45 |
–44 |
5 |
3 |
2 |
0 |
Среднее значение доходности индекса равно 2 %, а среднее значение доходности ценной бумаги А 0,7 %. По формуле (1.6) найдем ковариацию доходности индекса и ценной бумаги А:
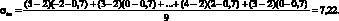
Найдем дисперсию доходности индекса по формуле (1.1). Ее значение будет равно 17,78. Тогда коэффициент бета по формуле (1.22) будет равен 0,4. Это означает, что доходность ценной бумаги будет меняться значительно меньше, чем рынок в целом. Так, при росте или падении индекса на 1 % доходность ценной бумаги А вырастет или снизится на 0,4 % соответственно. Такие ценные бумаги называют оборонительными, что подчеркивает их низкий уровень риска.
Общий риск актива можно представить в следующем виде:
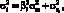 (1.23)
(1.23)
|
где |
дисперсия ошибок (отклонений фактических значений доходностей актива от значений, рассчитанных в соответствии с моделью). |
Для того чтобы аналитически задать , рассмотрим следующую линейную модель:
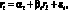 (1.24)
(1.24)
|
где ri – |
доходность актива i; |
|
rI – |
доходность индекса; |
|
?i, ?i – |
параметры модели; |
|
?i – |
случайная ошибка. |
Предположения относительно случайных ошибок ?i:
– ошибки независимы и одинаково распределены по нормальному закону распределения со средним 0 и постоянной дисперсией;
– ошибки независимы от rI.
Обозначим оценки параметров модели по методу наименьших квадратов через 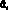 и
и  .
.  определяется по формуле 1.22, а
определяется по формуле 1.22, а 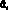 находим по следующей формуле:
находим по следующей формуле:
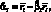 (1.25)
(1.25)
|
где |
средняя доходность актива i; |
|
|
средняя доходность индекса. |
Ошибки представляют собой отклонения фактических доходностей актива от значений, рассчитанных согласно модели:
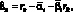 (1.26)
(1.26)
|
где rit – |
доходность актива i в момент времени t; |
|
rIt – |
доходность индекса в момент времени t. |
Искомая дисперсия случайной ошибки находится по формуле:
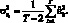 (1.27)
(1.27)
Очевидно, что представление для риска согласно формуле (1.23) верно только в случае независимости доходности рыночного портфеля (индекса) и случайной ошибки.
Таким образом, риск актива представляет собой величину, состоящую из двух элементов: рыночного риска 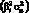 , определяемого бетой актива, и нерыночного риска
, определяемого бетой актива, и нерыночного риска 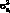 , являющегося уникальным для каждого актива.
, являющегося уникальным для каждого актива.
Перейдем от риска актива к риску портфеля. Бета портфеля ?p определяется по следующей формуле:
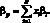 (1.28)
(1.28)
Нерыночный риск портфеля определяется по формуле:
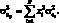 (1.29)
(1.29)
Тогда общий риск портфеля будет равен:
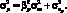 (1.30)
(1.30)
Общий риск портфеля можно переписать следующим образом:
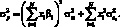 (1.31)
(1.31)
Так же как и риск актива, риск портфеля состоит из двух частей. Первая часть 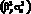 связана с общерыночными тенденциями, определяется коэффициентом бета портфеля и называется систематическим или рыночным риском, вторая часть
связана с общерыночными тенденциями, определяется коэффициентом бета портфеля и называется систематическим или рыночным риском, вторая часть 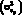 связана с индивидуальными рисковыми факторами, влияющими на доходность отдельных активов, и называется несистематическим или специфическим риском. При этом, чем больше активов включено в портфель, тем ниже общий риск портфеля за счет снижения несистематического риска. В пределе общий риск портфеля должен быть равен только рыночному риску, источником которого являются общерыночные факторы, влияющие на все активы. На рис. 1.11 проиллюстрирована данная концепция.
связана с индивидуальными рисковыми факторами, влияющими на доходность отдельных активов, и называется несистематическим или специфическим риском. При этом, чем больше активов включено в портфель, тем ниже общий риск портфеля за счет снижения несистематического риска. В пределе общий риск портфеля должен быть равен только рыночному риску, источником которого являются общерыночные факторы, влияющие на все активы. На рис. 1.11 проиллюстрирована данная концепция.
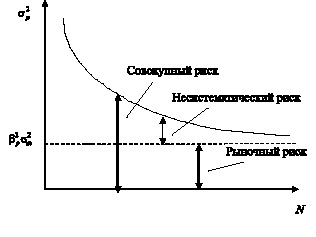
Рис. 1.11. Систематический и несистематический риск портфеля активов
При этом необходимо отметить, что достижение заданного уровня риска может быть реализовано с использованием различного количества активов. Однако, для снижения транзакционных издержек вследствие большого количество операций при формировании портфеля необходимо ориентироваться на корреляцию доходностей активов, т.к. как было отмечено выше, именно за счет включения в портфель активов, доходности которых максимально отрицательно коррелированы, можно достичь наименьшего показателя риска при меньшем количестве активов.
Продолжим изучение вопроса оценки риска с использованием стандартного отклонения. Выше мы говорили об оценке этого показателя на основе выборочных данных. В риск-менеджменте в качестве альтернативного названия стандартного отклонения используется также термин волатильность (volatility). Волатильность того или иного актива, оцененную на основе исторических данных, еще называют исторической волатильностью (historical volatility). Кроме исторической волатильности в риск-менеджменте используют также подразумеваемую волатильность (implied volatility). Подразумеваемая волатильность оценивается на основе рыночных цен торгуемых производных инструментов (опционов). Мы не будем здесь рассматривать подробно теоретические и практические вопросы, связанные с производными инструментами, с ними можно ознакомиться в специализированных источниках. В этой главе по мере необходимости изложения материала мы будем обращаться к соответствующим темам, связанным с производными инструментами. Для пояснения понятия подразумеваемая волатильность и то, как ее найти, необходимо обратиться к известной формуле ценообразования опционов Блэка-Шоулза, в соответствии с которой рассчитывается цена европейского опциона call на бездивидендную акцию:
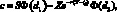 (1.32)
(1.32)
|
где S – |
текущая цена опциона; |
|
X – |
цена исполнения опциона; |
|
T – |
момент исполнения опциона; |
|
r – |
безрисковая доходность; |
|
?() – |
функция стандартного нормального распределения. |
В вышеприведенной формуле значения d1 и d2 определяются по формулам (1.33) и (1.34):
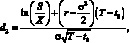 (1.33)
(1.33)
|
где c – |
цена европейского опциона колл; |
|
? – |
волатильность цены актива. |
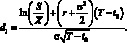 (1.34)
(1.34)
Как видно из приведенной формулы стоимости опциона волатильность цены акции является одной из ее составляющих. Для нахождения волатильности необходимо подставить в данную формулу все остальные известные параметры. Цена опциона является строго возрастающей функцией от волатильности. Каждому значению цены опциона соответствует единственное значение волатильности, которое можно найти численно. Подразумевая волатильность – это рыночная оценка волатильности базового актива опциона на текущий момент.
Поясним на числовом примере (1.7) расчет подразумеваемой волатильности на основе стоимости опциона на бездивидендную акцию. Предположим, что текущая цена акции равна 100 руб. Безрисковая процентная ставка составляет 8,25 % годовых. На основе исторической выборки цен акции определяем годовую волатильность доходности акции, пусть ее значение равно 20 % годовых. Найдем стоимость опциона call на данную акцию (базисным активом опциона является одна акция), при условии, что цена исполнения опциона составляет 115 руб., а срок до погашения полгода. Для нахождения стоимости данного опциона воспользуемся приведенной выше формулой Блэка-Шоулза. Для начала оценим значения d1 и d2:
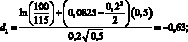
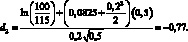
Далее найдем значение функции стандартного нормального распределения для найденных значений d1 и d2 (например, можно воспользоваться формулой программы Excel НОРМСТРАСП()):
?(–0,63) = 0,27;
?(–0,77) = 0,22.
Теперь найдем стоимость опциона call по формуле (1.32):
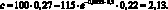
Таким образом, стоимость опциона call на бездивидендную акцию с ценой исполнения 115 руб. и текущей ценой 100 руб. должна быть равна 2,13 руб. При этом для оценки стоимости опциона мы нашли историческую волатильность доходности акции. Найденная стоимость опциона не является рыночной ценой, т.е. ценой, по которой с данным опционом совершаются сделки. Найденная стоимость опциона является оценкой рыночной цены опциона. Теперь рассмотрим задачу нахождения подразумеваемой волатильности доходности акции на основе рассмотренного опциона. Предположим, что рыночная цена опциона как раз равна 2,13 руб. Задача заключается в нахождении неизвестного значения волатильности при условии, что все остальные параметры, используемые в формуле Блэка-Шоулза, известны. Данная задача решается численными методами (для простоты можно воспользоваться стандартной возможностью программы Excel поиск решения). В результате решения данной задачи найденное значение подразумеваемой волатильности будет равно 20 % годовых.
Рассмотрим следующие два показателя, использующиеся при анализе денежных потоков. Эти показатели – дюрация (duration) и выпуклость (convexity). Дюрация и выпуклость являются мерами чувствительности потока платежей к изменению процентной ставки. Рассмотрим данные показатели на примере анализа облигаций. Облигацию можно представить как актив, дающий определенный денежный поток. Обозначим через CFt денежный поток по облигации в момент времени t. Текущая цена облигации P определяется как приведенная стоимость будущих денежных потоков по облигации:
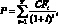 (1.35)
(1.35)
где i – доходность к погашению облигации.
Для купонной облигации дюрация определяется из следующего соотношения:
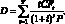 (1.36)
(1.36)
Экономическая интерпретация дюрации заключается в том, что данный показатель характеризует средневзвешенное время до погашения облигации. При этом весами выступают приведенные стоимости денежных потоков. Очевидно, что для бескупонных облигаций дюрация равна сроку до погашения T. Дюрацию, приведенная в формуле (1.35), еще называют дюрацией Маколея (Macaulayduration). Кроме дюрации Маколея рассчитывают модифицированную дюрацию:
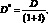 (1.37)
(1.37)
Модифицированная дюрация является мерой подверженности цены облигации риску изменению процентных ставок. Первая производная цены облигации по доходности равна:
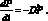 (1.38)
(1.38)
Изменение цены облигации связано с модифицированной дюрацией следующим соотношением:
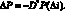 (1.39)
(1.39)
Как видно из данной формулы, чем больше модифицированная дюрация, тем больше изменяется цена облигации при изменении доходности. Иными словами, на величину изменения цены облигации оказывает влияние средневзвешенный срок до погашения облигации. Чем этот срок больше, тем большее изменение в ценах облигаций (падение или рост) происходит. В условиях ожидания тех или иных изменений доходности необходимо производить калибровку дюрации портфеля облигаций для того, чтобы обеспечить меньшую подверженность портфеля процентному риску (например, сокращать дюрацию портфеля облигаций в условиях ожидаемого роста доходности).
Выпуклость купонной облигации рассчитывается по следующей формуле:
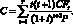 (1.40)
(1.40)
Для бескупонных облигаций выпуклость считается по формуле:
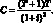 (1.41)
(1.41)
Выпуклость связана со второй производной цены облигации следующим соотношением:
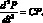 (1.42)
(1.42)
Используя данные соотношения, запишем изменение цены облигации через разложение в ряд Тейлора:
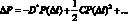 (1.43)
(1.43)
Таким образом, модифицированная дюрация является линейной аппроксимацией изменения цены облигации. Учет выпуклости при расчете изменения цены облигации позволяет учесть нелинейность взаимосвязи между ценой и доходностью.
Рассмотрим применение данных показателей на числовом примере (1.8). Рассмотрим бескупонную облигацию со сроком погашения 5 лет. Облигация торгуется на рынке с доходностью 10 % годовых. Ее текущая стоимость получена на основе формулы (1.35):
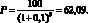
Дюрация Маколея совпадает со сроком до погашения 5 лет. Модифицированная дюрация рассчитывается по формуле (1.37):
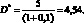
Выпуклость облигации находим по формуле (1.41):
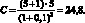
Произведем аппроксимацию изменения цены облигации с помощью дюрации и выпуклости в случае, если доходность увеличится на 1 до 11 %. Используя выражение (1.43) получаем:
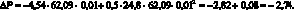
Как видно из приведенного расчета, учет только первой производной дает цену облигации в размере 62,09 – 2,82 = 59,27 руб., а использование и первой и второй производных дает цену немного выше: 62,09 – 2,82 + 0,08 = 59,35 руб. Теперь сравним полученные цены с точной ценой 59,34 руб. Очевидно, что использование только линейной аппроксимации дает большую ошибку, чем использование совместно и линейной и нелинейной аппроксимации.
Аналогично можно представить дюрацию и выпуклость для портфеля облигаций. Обозначим через wi вес облигации i в портфеле, который будем рассчитывать по следующей формуле:
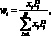 (1.44)
(1.44)
|
где xi – |
количество облигации i; |
|
Pi – |
цена облигации i; |
|
N – |
количество облигаций в портфеле. |
Тогда модифицированная дюрация портфеля облигаций 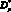 определяется по следующей формуле:
определяется по следующей формуле:
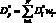 (1.45)
(1.45)
Аналогично определяем выпуклость портфеля облигаций Cp:
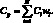 (1.46)
(1.46)
В финансовом риск-менеджменте выражение для аппроксимации изменения стоимости актива на основе разложения в ряд Тейлора является фундаментальным. Аналогичные подходы используются для аппроксимации изменения цен многих финансовых активов, в том числе производных финансовых активов, в частности опционов. В случае с опционами первые и вторые производные имеют тот же смысл, только отличаются назва-
нием – дельта и гамма соответственно. Более подробно с данным вопросом можно ознакомиться в специализированной литературе.
Следующий показатель, который мы рассмотрим, это показатель ValueatRisk (VaR). Данный показатель является одним из широко используемых показателей при оценке рисков. VaR был разработан банком J.P. Morgan и на его основе была предложена целая методология оценки рыночных рисков Risk Metrics, которая была обнародована в 1994 г. Позднее департамент банка, занимавшийся корпоративным риск-менеджментом, был выделен в отдельную компанию Risk Metrics Group, после чего новая компания провела первичную эмиссию акций и стала публичной. Нынешним владельцем компании является MSCI Inc. Всю необходимую техническую документацию, касающуюся методологии RiskMetrics, можно найти на сайте www.msci.com.
Рассмотрим, что представляет собой показатель VaR. VaR – это максимальная величина потерь за определенный временной интервал T при фиксированной доверительной вероятности p. Иными словами, VaR это величина убытков, которая не будет превышена с вероятностью p за время T. Поясним суть данного показателя на примере распределения прибылей и убытков. На рис. 1.12 представлена плотность распределения f(x) и интегральная функция распределения F(x) прибылей и убытков. Как видно из данного рисунка VaR представляет собой квантиль уровня 1 – p распределения (в данном случае 5 %) прибылей и убытков.
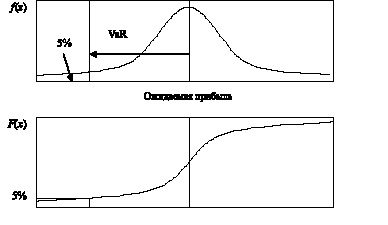
Рис. 1.12. VaR как квантиль распределения прибылей/убытков
На практике выделяют два показателя VaR. Один из них известен как абсолютный VaR, который определяет максимальные убытки при самом худшем сценарии развития ситуации с доверительной вероятностью p. Второй показатель – относительный VaR, рассчитывается как разница между ожидаемой прибылью/потерями и убытками при худшем сценарии с доверительной вероятностью p. Поясним их отличие на следующей примере. На рис. 1.13 представлено распределение прибылей и убытков. Для простоты будем считать, что прибыли и убытки распределены нормально.
Как видно из рисунка показатель VaR* соответствует максимальной величине убытков при доверительной вероятности 95 %. Доверительная вероятность определяется как:
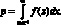 (1.47)
(1.47)
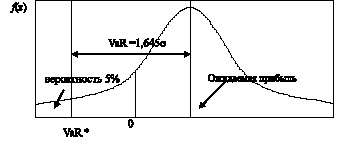
Рис. 1.13. Сравнение абсолютного и относительного VaR
Таким образом, существует 5 % вероятность того, что фактические убытки превысят VaR*. Этот показатель называют абсолютным VaR. Относительный VaR равен разнице между ожидаемой прибылью/убытком и VaR*. При условии равенства ожидаемой прибыли/убытка 0 эти два показателя равны. На практике, когда говорят о VaR, то имеют ввиду именно относительныйVaR. Кроме этого, в концепции экономического (или рискового) капитала, имеющей большое значение для банковской сферы, показатель VaR используется в своем втором значении.
Рассмотрим пример (1.9). Найдем VaR портфеля, состоящего из инвестиций в валюту, например доллар США, при доверительной вероятности 95 %. Случайной переменной является изменение долларовой стоимости портфеля. Пусть ожидаемое значение изменения стоимости портфеля равно ?. Предположим, что изменение стоимости портфеля нормально распределено. Квантиль распределения, соответствующий доверительной вероятности 95 % равен:
? – ??, (1.48)
где ? – квантиль стандартного нормального распределения уровня 1 – p.
Квантиль стандартного нормального распределения, соответствующего доверительной вероятности 95 %, равен –1,645. Найдем теперь VaR по следующей формуле:
? – (? – ??). (1.49)
Пусть стандартное отклонение портфеля равно 10 млн. долл., тогда потенциальное максимальное снижение портфеля при доверительной вероятности 95 % составит 1,645•10 млн. долл. = 16,45 млн. долл.
Если стандартное отклонение выражается в терминах доходности актива, а не в стоимостном выражении (как в предыдущем примере в долл. США), то VaR актива можно найти следующим образом:
VaRi = Pi??i, (1.50)
|
где Pi – |
стоимость актива i; |
|
?i – |
стандартное отклонение доходности актива i. |
Для оценки VaR большое значение имеет выбор временного интервала и доверительной вероятности. Временной интервал можно определить как ожидаемый срок нахождения инструмента в портфеле, на протяжении которого можно закрыть позиции без существенного убытка. Уровень доверия выбирается в зависимости от решения конкретной задачи и целей, которые необходимо достичь. Тем не менее, существуют рекомендательные значения для использования в тех или иных ситуациях. Например, в соответствии с рекомендациями RiskMetrics временной интервал для оценки рыночного риска с помощью показателя VaR составляет один день при доверительной вероятности 95 %. В соответствии с рекомендациями Базельского комитета по банковскому надзору при Банке международных расчётов используется десятидневный временной горизонт (десять рабочих дней или две календарные недели) и 99 % уровень доверия.
При оценке стандартного отклонения доходности для разных временных горизонтов используется поправка на корень квадратный из времени. Так, для нахождения годового стандартного отклонения доходности по известному дневному значению, необходимо дневное стандартное отклонение доходности умножить на  . В данном случае 250 означает среднее количество торговых дней в году.
. В данном случае 250 означает среднее количество торговых дней в году.
Рассмотрим следующий пример (1.10). Дан портфель, состоящий из инвестиций в акции компании А, текущая стоимость портфеля равна 10 млн. руб. Годовое стандартное отклонение доходности акции составляет 30 % годовых. Доходность акции распределена нормально. Определим однодневныйVaR портфеля. Найдем дневное стандартное отклонение доходности акции в соответствии с правилом, описанным выше:
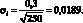
Т.е. значению годового стандартного отклонения доходности акции, равному 30 %, соответствует дневное стандартное отклонение доходности в размере 1,89 %. Далее, воспользуемся формулой (1.50) для вычисления однодневного VaR портфеля:
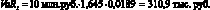
Таким образом, с вероятностью 95 % стоимость портфеля за следующий торговый день может снизиться не более чем на 310,9 тыс. руб.
Рассмотрим теперь VaR портфеля, состоящего из нескольких активов. Логика вычисления VaR портфеля аналогична вычислению VaR отдельного актива. VaR портфеля (VaRp) будем определять по следующей формуле:
VaRp = Pp??p, (1.51)
|
где Pp – |
стоимость портфеля; |
|
?p – |
стандартное отклонение доходности портфеля. |
Для портфеля, состоящего из двух активов, с учетом формулы (1.8) для дисперсии портфеля, оценка VaR примет следующий вид:
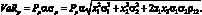 (1.52)
(1.52)
Сделаем некоторые преобразования:
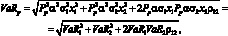 (1.53)
(1.53)
где VaR1, VaR2 – оценка VaR для первого и второго активов.
Как следует из приведенной выше формулы оценки VaR для первого и второго активов можно выразить следующим образом:
 (1.54)
(1.54)
где P1 – стоимость первого актива.
 (1.55)
(1.55)
где P2 – стоимость первого актива.
Формула (1.53) может быть распространена на случай n активов:
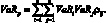 (1.56)
(1.56)
Рассмотрим следующий пример (1.11). Портфель состоит из инвестиций в акции двух компаний А и Б. Доля акции компании А в портфеле 30 %, компании Б – 70 %. Однодневные стандартные отклонения доходности акций компании А и Б равны 1,5 и 2 % соответственно. Доходности акций нормально распределены. Корреляция доходностей акций составляет 0,6. Стоимость всего портфеля равна 10 млн. руб. Найдем однодневный VaR портфеля при доверительной вероятности 95 %. Используя формулу (1.8), находим дисперсию доходности портфеля. Подставляя все известные данные, мы получим дисперсию в размере 2,9185. Извлекая квадратный корень из дисперсии, найдем однодневное стандартное отклонение портфеля – 1,7 %. Подставляя значение стандартного отклонения в формулу (1.51) найдем искомую оценку VaR портфеля:
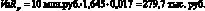
Таким образом, стоимость портфеля в течение следующего торгового дня не снизится более чем на 279,7 тыс. руб. при 95 % уровне доверия.
В приведенных выше примерах мы предполагали, что законы распределения активов и ковариационные матрицы доходностей активов заданы. При этом доходности активов распределены по нормальному закону распределения. Метод расчета VaR, основанный на данных предположениях, известен как параметрический или дельта-нормальный. Однако у данного метода есть существенные недостатки. Основной недостаток связан с предположением о нормальности распределения доходностей. На практике распределения доходностей не следуют нормальному распределению, а демонстрируют различного рода отклонения от данного закона. В частности, ассимитричность, островершинность или наоборот более пологий наклон ветвей распределения (т.н. проблема толстых «хвостов»). Кроме параметрического метода существует еще два метода оценки VaR: исторический и метод Монте-Карло. В соответствии с историческим методом оценки VaR анализируемое распределение стоимости портфеля получают на основе исторической выборки значений доходности и построения гистрограммы распределения частот. При использовании данного метода критическим показателем становится объем выборки. Недостатком исторического метода является предположение о том, что историческое распределение доходности является лучшим распределением будущих значений доходности. Метод Монте-Карло относится к методам имитационного моделирования. Результат применения данного метода представляет собой распределение стоимости портфеля, полученное путем неоднократного итерированного процесса моделирования. При использовании данного метода критическим является требование к вычислительной мощности. Кроме этого, существенным недостатком данного метода является т.н. модельный риск. Допущение о нормальном распределении необходимо в дельта-нормальном методе, в методе Монте-карло и историческом методе этого не требуется.
Методы оценки риска на основе VaR были разработаны для оценки рисков банковских портфелей. На сегодняшний день эти методы используются и в других финансовых институтах. В дальнейшем, данные методы получили свое распространение и в среде нефинансовых организаций, где особое значение с точки зрения риска имеет денежный поток. В результате была предложена мера риска Cashflowatrisk (CFaR), которая по аналогии с VaR оценивает наихудший сценарий развития ситуации – в данном случае наименьший денежный поток из-за неблагоприятного влияния рыночных факторов риска за определенный временной интервал при заданном уровне доверительной вероятности. В качестве примера неблагоприятного влияния рыночного фактора риска на денежный поток компании можно привести снижение экспортной выручки от укрепления национальной валюты.
Некоторые исследователи относят кнедостаткомVaR как меры риска то, что VaR не является когерентной мерой риска (не обязательно выполнение свойства субаддитивности), кроме того VaR не учитывает распределение доходности портфеля за пределами VaR. В качестве альтернативного показателя риска, позволяющего исправить последний недостаток показателя VaR и учесть потери за пределами VaR, является показатель ожидаемых потерь. В зарубежной литературе по проблематике рисков он имеет несколько названий, в т.ч. Expected Shortfall (ES), Conditional VaR (CVaR), Average value at risk (AVaR), Expected tail loss (ETL). В то время как VaR показывает уровень максимальных потерь при заданном уровне доверительной вероятности, показатель ожидаемых потерь позволяет оценить ожидаемый убыток в том случае, если VaR будет превышен. Т.е. если мы говорим об оценке VaR с доверительной вероятностью 95 %, то Expected Shortfall показывает ожидаемые потери в оставшихся 5 % случаев.
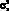 –
–
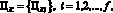 –
–
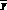 –
–
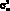 –
–
 –
–
 –
–