Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ФИНАНСОВЫЙ АНАЛИЗ: РИСКИ, КРЕДИТОСПОСОБНОСТЬ, ИНВЕСТИЦИИ

Бороухин Д. С., Царева С. В., Гапоненкова Н. Б., Мотина Т. Н., Бреславец И. Н., Беспалова С. В., Дрождинина А. И., Скотаренко О. В., Смирнов А. В., Рапницкая Н. М., Кибиткин А. И.,

1.4. Методы анализа предпринимательских и финансовых рисков

В данном параграфе мы рассмотрим некоторые используемые на практике методы анализа предпринимательских и финансовых рисков.

Одними из простых, но при этом эффективных методов анализа рисков являются анализ чувствительности и анализ безубыточности. Анализ чувствительности заключается в оценке влияния изменений одного или нескольких исходных параметров на результирующий показатель. Так, например, анализ чувствительности некоторого инвестиционного проекта может заключаться в оценке влияния изменения основных параметров этого проекта на показатели его эффективности. Анализ чувствительности предполагает построение определенной финансовой модели проекта, связывающей исходные параметры и результирующий показатель согласно заданному алгоритму. Результатом анализа чувствительности является значение или интервал возможных значений результирующего показателя при изменении исходных параметров в заданных пределах. При этом используются как абсолютные, так и относительные значения. Как правило, при проведении анализа чувствительности не учитываются взаимосвязи между исходными параметрами. Однако на практике такой подход может привести к ошибочным выводам.

Рассмотрим анализ безубыточности и анализ чувствительности на следующем примере (1.12). Найдем минимальный (безубыточный) объем продаж рыбной продукции. Запишем выражение для нахождения операционной прибыли:

П = P•Q – VC•Q – FC, (1.57)

Тогда безубыточный объем реализации продукции будем равен:

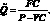(1.58)

Пусть, даны следующие исходные условия: цена реализации единицы продукции 20 руб., удельные переменные издержки 10 руб., общий объем постоянных расходов 100 000 руб. Тогда безубыточный объем реализации:

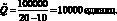
Ответим на следующий вопрос: на сколько увеличится прибыль, если объем реализации увеличится на 1000 единиц? В этом случае увеличение прибыли составит:

??Q = ?Q•(P – VC). (1.59)

Для нашего примера увеличение объема реализации на 1000 единиц приведет к увеличению прибыли на 10 000 руб. На рис. 1.14 показана динамика затрат, выручки и прибыли. Прибыль изменяется линейно относительно объема реализации.

Таким образом, мы нашли минимальный объем реализации и выяснили, как будет меняться операционная прибыль при изменении объема реализации. Однако на практике такого упрощенного подхода, когда при изменении объема реализации остальные параметры остаются постоянным, как правило, бывает недостаточно. Изменение объема предложения должно сказываться на отпускных ценах. Пусть объем реализации и цена связаны следующим соотношением:

P = –0,1Q + 250. (1.60)

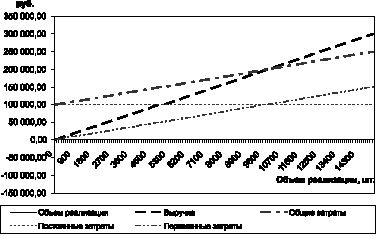
Рис. 1.14. Динамика затрат, выручки и прибыли в зависимости от изменения объема реализации

Тогда, общая величина прибыли будет равна:

(1.61)

Для нашего примера выражение для операционной прибыли примет вид:

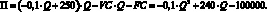(1.62)

В отличие от соотношения (1.57), теперь выражение для прибыли представляет собой квадратное уравнение. Найдем объем реализации, при котором прибыль равна нулю (безубыточный объем реализации). Для квадратного уравнения таких решений будет два. Для нашего примера целочисленными решениями уравнения (1.62) являются значения объемов реализации 536 и 1863. В отличие от линейного уравнения прибыли, подразумевающего, что прибыль может расти бесконечно при увеличении объема реализации, для квадратного уравнения (1.62) существует объем реализации, при котором прибыль достигает максимального значения. В нашем случае:

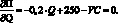
Откуда получаем:

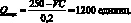
Ответим на вопрос: на сколько увеличится прибыль при увеличении объема реализации на X единиц? В отличие от линейного уравнения прибыли, где увеличение объема реализации сопровождалось пропорциональным ростом прибыли, для квадратного уравнения прирост прибыли будет разным в каждой точке, соответствующей определенному объему реализации. На рис. 1.15 представлена динамика затрат, выручки и прибыли в случае учета взаимосвязи между объемом реализации и отпускными ценами.

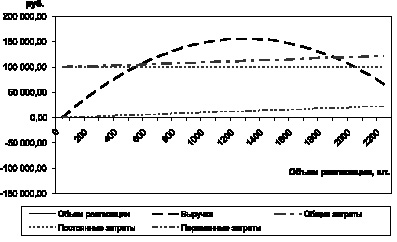
Рис. 1.15. Динамика затрат, выручки и прибыли в случае линейной взаимосвязи между объемом реализации и ценой продаж

Дальнейшим развитием анализа чувствительности являются сценарный анализ и имитационное моделирование. Сценарный анализ заключается в разработке сценариев развития ситуации, учитывающих взаимосвязи между различными факторами, и расчет показателей эффективности для каждого сценария. Данный метод существенно дополняет возможности по анализу рисков и позволяет посмотреть на проблему комплексно. Каждый сценарий представляет собой одно из возможных состояний среды в будущем и позволяет оценить, как будет функционировать система в случае реализации того или иного сценария. Если сценарный анализ предполагает разработку нескольких сценариев возможных состояний среды и оценку эффективности функционирования системы в каждом сценарии, то имитационное моделирование позволяет смоделировать динамику всей системы, изучить ее поведение при всевозможных изменениях среды. В результате применения данного метода исследователь получает не отдельные дискретные значения анализируемых показателей, а целое распределение значений показателей. Имитационное моделирование относится к численным методам и используется тогда, когда аналитическое выражение для решения определенной задачи получить невозможно или крайне
затруднительно.

Отдельным методом анализ рисков является метод стресс-тестирования. Стресс-тестирование представляет собой инструмент оценки потенциальных потерь объекта исследования (например, финансовые результаты проекта, стоимость портфеля активов, финансовое состояние компании) в условиях, выходящих за пределы нормального его функционирования. Стресс-тестирование оценивает потенциальное воздействие на объект исследования критических, стрессовых изменений исходных параметров (факторов риска). Стресс-тестирование позволяет моделировать воздействие или эффект исключительных, маловероятных, но при этом потенциально возможных событий. Как правило, в моделях стресс-тестирования учитываются не отдельные рисковые факторы, а их комбинации. В качестве основных методов стресс-тестирования применяются однофакторные (анализ чувствительности) и многофакторные стресс-тесты (сценарный анализ). Менее популярны методы оценки максимальных потерь и методы, основанные на теории экстремального значения.

Особое место в анализе рисков занимает теория игр. Теория игр является широко распространенной теоретической концепцией, имеющей непосредственное прикладное значение. Впервые математические аспекты теории игр были представлены в книге фон Неймана и Моргенштерна «Теория игр и экономическое поведение» в 1944г. Применительно к экономической науке теория игр представляет собой математический метод исследования и принятия оптимальных решений в условиях неопределенности, наличия конфликта интересов и конкурирующих стратегий поведения участников с целью достижения наилучшего результата. Каждая сторона (игрок) реализует определенную стратегию, которая характеризуется набором исходов (прибыли, убытки), ее конкретный результат зависит от того, какую стратегию избрали конкуренты. Основная цель использования теории игр для решения практических задач заключается в выборе оптимальной стратегии поведения в условии конфликта (конкуренции) с другими игроками (сторонами, конкурентами) для достижения в среднем более высокого выигрыша. В условиях неопределенности для выбора наилучшей стратегии поведения в теории игр используют следующие критерии:

– критерий гарантированного результата (максиминный критерий Вальда) – данный критерий обеспечивает максимальный выигрыш из всех минимальных выигрышей, или иначе минимальный убыток из всех максимальных потерь;

– критерий оптимизма (максимакса) – данный критерий обеспечивает получение максимального выигрыша из всех максимальных выигрышей, или иначе минимальный убыток из всех минимальных убытков;

– критерий пессимизма;

– критерий Сэвиджа – аналогичен критерию Вальда, применяется только для матрицы рисков (упущенных возможностей) и позволяет минимизировать потери;

– критерий Гурвица – в соответствии с данным критерием выбор осуществляется как комбинация самого оптимистичного и пессимистичного решения. Критерий Гурвица применяется как к матрице выигрышей, так и рисков.

Рассмотрим использование данных критериев для выбора оптимальных стратегий на следующем примере (1.13). Предположим, что некая компания планирует запустить производство новой продукции. Компания разработала три стратегии производства. Однако, спрос на новую продукцию неизвестен. На основе проведенных маркетинговых исследований был спрогнозирован уровень спроса в трех вариантах: пессимистичный, реалистичный, оптимистичный. Зададим следующую платежную матрицу:

Таблица 1.6

Платежная матрица стратегий производства

Данная платежная матрица представляет собой таблицу, в которой каждый ее элемент – прибыль (?ij), соответствующая выбранной стратегии производства Bi при реализации j-го варианта прогноза спроса (Cj). Данный вариант задачи выбора оптимальной стратегии поведения в теории игр получил название игры с «природой».

Найдем наилучшие производственные стратегии, удовлетворяющие вышеперечисленным критериям. Начнем с критерия Вальда. Данный критерий можно задать следующим образом:

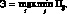(1.63)

С помощью данного критерия выбирается стратегия производства, обеспечивающая минимально гарантированную прибыль. Для этого определяется минимальная прибыль каждой стратегии производства: –30, 50, –20. Далее выбирается максимальное из полученных значений. Таким образом, в соответствии с данным критерием выбор делается в пользу стратегии производства B2, обеспечивающей гарантированную прибыль в размере 50 руб.

При использовании критерия максимакса выбирается стратегия, дающая максимальную прибыль. Данный критерий записывается следующим образом:

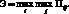(1.64)

Для выбора стратегии на основании данного критерия найдем максимальную прибыль для каждого варианта стратегии производства: 100, 200, 50. Далее, выберем стратегию, соответствующую максимальной из полученных значений прибыли. Таким образом, критерию максимакса соответствует стратегия и значение прибыли 200 руб.

Следующий критерий – критерий пессимизма, который записывается следующим образом:

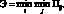(1.65)

В данном случае выбирается стратегия, прибыль которой наименьшая среди всех стратегий. Такой стратегией является стратегия B1, которой соответствует минимальная прибыль –30 руб.

Для выбора оптимальной стратегии в соответствии с критерием Сэвиджа необходимо платежную матрицу, приведенную в табл. 1.6, преобразовать в матрицу рисков. Элементами матрицы рисков являются значения (риски), которые определяются следующим образом:

(1.66)

где ?maxj – наибольшая прибыль, соответствующая уровню спроса Cj.

Т.е. риск в данной ситуации представляет собой разницу между прибылью, которую компания могла бы получить в случае, если бы точно знала, что уровень спроса будет соответствовать Cj, и той прибылью, которую компания получит при отсутствии возможности точного прогнозирования спроса. Критерий Сэвиджа определяется следующим образом:

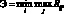(1.67)

Таким образом, критерий Сэвиджа соответствует критерию гарантированного результата Вальда с той лишь разницей, что применяется к матрице рисков. Продолжим рассмотрение примера. Преобразуем платежную матрицу в табл. 1.6 в матрицу рисков(табл. 1.7).

Таблица 1.7

Матрица рисков стратегий производства при неопределенном спросе

Находим максимальный риск, соответствующий каждой стратегии производства: 230, 50, 150. Далее, выбирается стратегия производства, чей риск является наименьшим из найденных значений. Таким образом, выбирается стратегия B2, риск которой равен 50 руб.

Критерий Гурвица является компромиссным критерием, усредняющим критерии крайнего оптимизма и пессимизма. Критерий выбора оптимальной стратегии Гурвица записывается следующим образом:

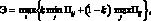(1.68)

где k – коэффициент пессимизма.

Если k = 0, то критерий Гурвица будет соответствовать критерию крайнего оптимизма, если k = 1 – то критерию Вальда. Конкретные значения коэффициента k выбираются между 0 и 1, и определяются в зависимости от конкретной задачи и склонности к риску. Продолжим рассматривать наш пример. Пусть k = 0,4. Найдем для каждой стратегии линейную комбинацию из минимальной и максимальной прибыли в соответствии с выражением 1.68: 48, 140, 22. Таким образом, в соответствии с критерием Гурвица оптимальной стратегией производства является стратегия B2, которой соответствует максимальное из полученных значений – 140 руб.

Рассмотрим следующий метод анализа рисков и принятия решений в условиях неопределенности – метод дерева решений. Название метода связано с соответствующим графическим представлением последовательности операций и решений, а также состояний среды с присваиванием каждому возможному состоянию среды вероятностей и значений исходов (выигрышей или проигрышей). Данный метод используется в задачах, в которых существует несколько возможных решений, при этом каждое конечное решение связано с определенной последовательностью промежуточных решений. Использование данного метода применительно к конкретной задаче подразумевает выполнение следующих этапов:

– формулирование задачи;

– построение дерева решений;

– оценка вероятностей состояний среды;

– определение исходов (выигрышей или проигрышей) для каждого состояния среды;

– решение задачи.

Рассмотрим применение данного метода на следующем примере (1.14). Транспортная компания приняла решение о расширении операций и приобретении дополнительно 10 автомобилей. Стоимость одного автомобиля равна 100 тыс. руб. Компания ожидает, что в первый год рост продаж будет высоким с вероятностью 0,6 и низким с вероятностью 0,4. В последующие 4 года рост продаж будет высоким с вероятностью 0,9 при условии, что в первый год он также был высоким, и с вероятностью 0,7 рост продаж будет низким при условии, что в первый год он также был низким. В случае высокого роста продаж суммарный годовой доход составит 500 тыс. руб., а в случае низкого роста продаж – 200 тыс. руб. Компания вместо приобретения автомобилей рассматривает возможность их аренды. Условия аренды предусматривают единовременную плату в размере 100 тыс. руб. за все 10 автомобилей плюс 30 % от годового дохода в течение 5 лет. Остаточная стоимость автомобилей не учитывается. Доходность операций компании составляет 10 % годовых. Используя метод дерева решений, найдем какой вариант приобретения автомобилей для компании будет предпочтительным. На рис. 1.16 показано дерево решения данной задачи.

Значения, представленные в правой части дерева решений, равны суммарным доходам за период со второго по пятый годы в текущих ценах, т.е. приведенных к настоящему моменту времени. В частности, значение в узле Ж дерева решений рассчитывается как:

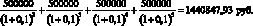
Значение в узле З определяется схожим образом:

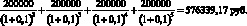
Аналогично определяются суммы приведенных доходов для узлов с И по О. Далее найдем ожидаемые значения приведенных доходов для узлов В, Г, Д и Е с учетом найденных значений приведенных доходов и заданных вероятностей роста продаж. Для узлов В и Д ожидаемое значение приведенного дохода будет равно:

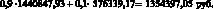
Для узлов Г и Е ожидаемый приведенный доход будет равен:

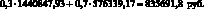
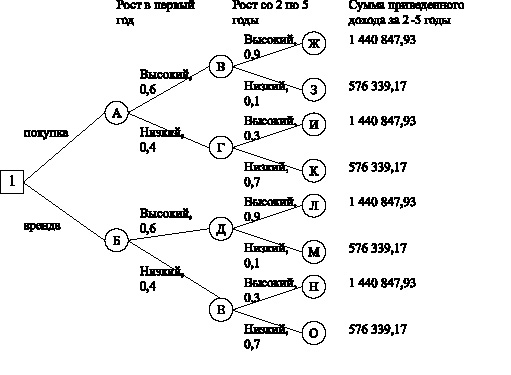
Рис. 1.16. Дерево решений задачи выбора между покупкой иди арендой автомобилей

С учетом полученного дохода в первый год скорректируем общую сумму приведенного дохода для узлов В, Г, Д и Е. Для узлов В и Д она составит:

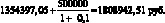
Соответственно для узлов Г и Е общая сумма приведенного дохода будет равна:

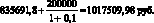
Теперь найдем ожидаемый приведенный доход в узлах А и Б. Как нетрудно заметить он будет одинаковым для обоих узлов дерева решений:

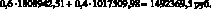
Чистый ожидаемый доход в узле А с учетом стоимости приобретения автомобилей будет равен:

Чистый ожидаемый доход в узле Б с учетом затрат на аренду автомобилей будет равен:

Таким образом, аренда является наиболее предпочтительным способом приобретения автомобилей, т.к. он максимизирует чистый ожидаемый доход компании.

Одним из широко используемых на практике инструментов анализа рисков является матрица вероятности и последствий рисков. Данная матрица позволяет в наглядном виде представить и ранжировать идентифицированные риски в зависимости от потенциального размера ущерба и вероятности наступления. Данная матрица предоставляет возможность не только идентифицировать все риски компании в координатах вероятность-последствие, но и выработать стратегию управления конкретными рисками в зависимости от вероятности их наступления и размера ущерба.

В условиях неполноты и недостоверности имеющейся в наличии информации использование методов анализа и оценки рисков, основанных на статистических методах, является затруднительным. В этом случае на практике прибегают к экспертным методам, когда для получения количественных оценок рисков используются мнения и суждения экспертов. Недостатками применения экспертных методов анализа рисков являются субъективность оценок и отсутствие строго математического доказательства оптимальности решений.