Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

4.1.2. Нечеткие данные, возникающие в процессе математического моделирования

4.1.2.1. Понятие нечеткого множества

Продолжая обсуждать проблему неопределенности, отметим, что она неизбежно возникает при моделировании сложных систем, где человек играет активную роль. Для получения существенных выводов о поведении сложной системы необходимо в принципе отказаться от высоких стандартов точности и строгости, которые характерны для сравнительно простых систем. Как отмечено выше, эффективная методология для такого отказа (теория нечетких множеств) была предложена Л. Заде [31].

В основе теории Л. Заде лежит достаточно очевидный факт – объективные представления о цели всегда нечетки. Но он делает и следующий шаг – полагает, что и все оценки субъекта и ограничения, с которыми он работает, также, как правило, нечетки, а иногда и вообще лишены в своем начальном виде количественных характеристик. Так он приходит к понятию лингвистической переменной – красное, не очень красное, совсем не красное и т.п. – а затем вводит некоторую функцию принадлежности, как способ формализации субъективного смысла этих качественных показателей.

Категория нечеткости и связанные с ней модели и методы очень важны с мировоззренческой точки зрения, поскольку с их появлением стало возможно подвергать количественному анализу те явления, которые раньше либо могли быть учтены только на качественном уровне, либо требовали использования весьма грубых моделей.

В обычной теории множеств существуют несколько способов задания множества. Одним из них является задание с помощью характеристической функции, определяемой следующим образом. Пусть  – так называемое универсальное множество, из элементов которого образованы все остальные множества, рассматриваемые в настоящей задаче, например, множество всех целых чисел, множество всех гладких функций, заданных на действительной оси, т.д. В дальнейшем в качестве универсального чаще будет, как правило, использовано множество действительных чисел, реже – множество вербальных значений, отражающих качественные значения. Характеристическая функция множества  – это функция , значения которой указывают, является ли  элементом множества :

Особенностью этой функции является бинарный характер ее значений – либо 1 либо 0.

С точки зрения характеристической функции нечеткие множества (НМ) являются естественным обобщением обычных множеств, когда мы отказываемся от бинарного характера этой функции и предполагаем, что она может принимать любые значения из отрезка [0, 1]. В теории НМ характеристическая функция называется функцией принадлежности (элемента  нечеткому множеству ), а ее значение  – степенью принадлежности элемента  НМ , где  – элемент универсального множества  [64], [76].

Более строго, нечетким множеством  называется совокупность пар , где элементы  называются носителями НМ [13], а  – это функция принадлежности вида : . Если носитель имеет лингвистическое значение, то его называют термом. Функция принадлежности определяет субъективную степень уверенности эксперта в том, что рассматриваемый носитель  соответствует содержательному смыслу данного НМ. Например, определить значения НМ С=«средняя урожайность» и В=«высокая урожайность» можно так:

, .

Эти функции не стоит путать с вероятностями, которые носят объективный характер и подчиняются другим математическим зависимостям. На рис.4.1 отражено, как одни и те же носители могут участвовать в определении различных НМ.

Важно отметить, что в реальном моделировании смысловая интерпретация функции принадлежности не является универсальной. Действительно, рассмотрим два случая. Пусть в первом случае  представляет градацию урожайности определенной сельскохозяйственной культуры, где   представляет интервал значений, соответствующих низкой (средней, высокой) урожайности;  – множество действительных чисел, представляющее область значений потенциально возможной урожайности для рассматриваемой ситуации. Тогда, говоря о прогнозируемой урожайности  в следующем году, нечеткое множество  можно трактовать следующим образом: ожидаемая урожайность окажется низкой в малой степени, средней – в несколько большей степени и высокой – в значительной степени.

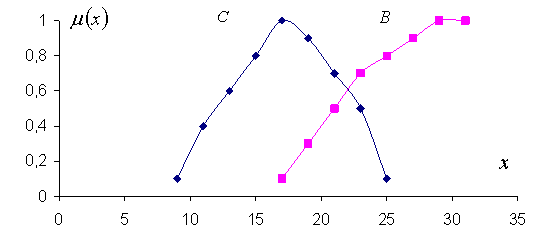
 Рисунок 4.1. Графическое представление нечетких множеств С и В

Во втором случае рассмотрим лингвистическую переменную «возраст», которая может принимать следующие значения: , , , ,  и другие – в зависимости от требуемой степени детального описания. Ясно, что переменная «возраст» будет обычной переменной, если ее значения представляют собой точные числа; лингвистической она становится будучи использована в нечетких рассуждениях человека. Так, лингвистическому значению  (около 20 лет) может соответствовать функция принадлежности, приведенная на рис.4.2.

Таким образом, в первом случае функция принадлежности выполняет роль вероятности, а во втором случае она выполняет роль «размытой» характеристической функции определенного качества.

 Рисунок 4.2. Графическое представление функции принадлежности терма «молодой»

 Коротко остановимся на понятии лингвистической переменной [19], [32]. Не вдаваясь в тонкости, ее можно определить как переменную, значениями (термами) которой являются не числа, а слова или предложения естественного (или формального) языка. Например, лингвистическая переменная «рост» определяется через множество термов {карликовый, низкий, средний, высокий, очень высокий}.

Для каждого терма  лингвистической переменной  определено численное значение  функции принадлежности, которое отражает степень соответствия этого терма содержательному смыслу лингвистической переменной, т.е. нечеткому множеству .

Сопоставляя рассмотренные выше случаи, нетрудно увидеть различия в смысловой трактовке соответствующих им функций принадлежности. В первом случае она имеет вероятностный характер, отражая по существу вероятность появления каждого из событий ,  или . Во втором случае каждому терму  соответствует определенное нечеткое множество со своей функцией принадлежности, которая описывает совместимость этого терма с различными числовыми значениями точек оси абсцисс на рис.4.2.

Пример аналитического задания функции принадлежности можно представить выражением

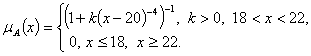
Это выражение задает функцию принадлежности для представления терма «возраст, очень близкий к двадцати».

Ясно, что конкретный вид функции принадлежности (и значения входящих в нее параметров) носит в значительной мере субъективный характер. Уменьшить степень этой субъективности можно, используя метод экспертных оценок, суть которого состоит в том, что как вид функции принадлежности, так и значения соответствующих параметров являются результатом коллективного творчества группы специалистов в рассматриваемой области – экспертов.

Пусть, например, решается задача определения значения некоторого параметра . В простейшем случае каждым из  экспертов назначается свое значение этого параметра – , затем эти числа усредняются

и полученный результат используется в качестве значения параметра . В соответствии со степенью опытности экспертов им могут быть присвоены веса , с учетом которых предыдущая формула усложняется:

,

где . Более детально с методом экспертных оценок можно ознакомиться в работах [93], [97].

В качестве второго подхода к определению конкретной функции принадлежности можно назвать приближенные значения эмпирической функции распределения. Этот подход тесно примыкает к такому разделу статистического анализа, точнее, статистического оценивания, как «проблема малых выборок» [24]. Предложенный в [8] метод построения функции принадлежности сочетает в себе вероятностный подход с процедурой парного сравнения степеней принадлежности, полученными от индивидуальных экспертов. Краткое описание различных подходов к определению функции принадлежности можно найти в [32], [81].

Заслуживает внимания статья [6], посвященная взаимосвязи между интервальной математикой и теорией нечетких множеств. Связь между интервальной математикой и теорией НМ очевидна в общем случае, а также в арифметике, логике и в исследованиях математических неопределенностей. Многие исследователи по сегодняшний день используют интервальную математику в теории нечетких множеств. Влияние нечеткой теории на интервальную математику не совсем очевидно. Вместе с тем результаты, полученные в теории нечетких множеств, используют в исследованиях, относящиеся к области интервальной математики. Кажущиеся различия между ними возникли в силу того, что основные направления интервальной математики и теории нечетких множеств развивались параллельно, практически не пересекаясь. Теория приближений независимо развилась из того, что было известно в обобщенном интервальном анализе, и, вместе с тем, она может быть использована в обобщенной теории нечетких множеств. Отметим, что интервальный анализ зарождался как метод моделирования и учета погрешностей, возникающих в результате компьютерных вычислений.

Следует отметить публикации [13], [19], посвященные применению интервальных методов в теории нечетких множеств. Можно также утверждать, что эти  области являются взаимодополняющими. Кроме того, сегодня уже есть достаточно много работ, посвященных методам оптимизации как в области интервального анализа, так и в теории нечетких множеств. Эти работы устанавливают взаимосвязь задач с интервальными данными и нечеткими данными.

4.1.2.2. Проблема определения операции над нечеткими множествами

Над нечеткими множествами можно производить различные операции, при этом необходимо определить их так, чтобы в частном случае, когда нечеткое множество является четким (обычным), эти операции переходили в обычные операции теории множеств, то есть операции над нечеткими множествами должны обобщать соответствующие операции над обычными множествами. При этом обобщение может быть реализовано различными способами, из-за чего какой-либо операции над обычными множествами может соответствовать несколько операций в теории нечетких множеств.

В задачах дискретного программирования, рассматриваемых в настоящей работе, используются две бинарные операции: суммирование исравнение с целью определения отношения >, < или =. Проанализируем степень пригодности или адекватности этим задачам существующих определений этих операций, представленных в известных к настоящему времени публикациях. При этом отметим, что нечеткие переменные принято делить на нечисловые и числовые, причем, последние принято называть нечеткими числами (НЧ).

В работе [32] представлены 3 аксиоматически определенных метода суммирования НМ  и  в полном пространстве :

  - алгебраический : ;

  - граничный :  для ;

  - драстический : , если  , если   и  в других случаях.

Каждый из этих методов, что принципиально важно, представляет собой некий вариант теоретико-множественного суммирования, т.е. сумма двух НМ и есть либо теоретико-множественное объединение их терм-множеств, либо некоторая его модификация. Можно утверждать, что представленные выше три метода суммирования НМ принципиально не соответствуют содержательному смыслу суммирования нечетких чисел (НЧ)  в целевых функциях вида , , например, задач землепользования. Отсюда вытекает необходимость предлагать и обосновывать новое определение операции суммирования НЧ в целевых функциях от допустимых решений  рассматриваемых задач, в частности, экстремальных задач на графах, взвешенных нечеткими числами.

В большинстве литературных источников операция суммирования НМ или НЧ рассматривается по сути как теоретико-множественное объединение. В [13], [32] осуществлена попытка замены теоретико-множественного сложения следующим видом суммирования. Следуя [13], [32], рассмотрим два НЧ  и , для которых определены соответственно два множества-носителя  и . Для элементов этих множеств априори известны дискретные функции принадлежности  и , . Предполагая, что множества  и  упорядочены по возрастанию, получаем множество-носитель для суммы носителей НЧ , представляющее собой такое упорядоченное по возрастанию множество , в котором , ,..., .

Определение функции принадлежности  элементов в сумме  представим на примере одного элемента . В процессе суммирования представителей носителей нечетких весов  и  элемент  может получаться в результате сложения элементов определенных  пар: , , , . Тогда степень принадлежности элемента  в  определяется согласно следующего выражения [13], [32]

 (4.1)

удовлетворяющего общепринятому свойству меры принадлежности: . Таким образом, множество и определенная для его элементов функция принадлежности ,  представляют собой НЧ, являющееся нечетким множеством.

Отметим, что определение (4.1) является уже четвертым по счету. В качестве иллюстративного примера неадекватности такого способа суммирования содержанию рассматриваемой задачи землепользования рассмотрим два конкретных НЧ, представляющих урожайность озимой пшеницы на пахотных угодьях одного хозяйства:

 (4.2)

В выражении (4.2) веса  и  представляют собой ожидаемые урожайности, т.е. ожидаемые урожаи, которые могут быть получены с единичной площади 1 га на двух различных полях. Согласно (4.2) ожидается: низкий урожай ц/га с функцией принадлежности (ФП) ; средний урожай  ц/га с ФП  и высокий урожай  ц/га с ФП . Тогда содержательно непротиворечивым суммированием этих двух одинаковых урожайностей является выражение

 (4.3)

Содержательный смысл выражения (4.3) состоит в том, что на площади  ожидается следующий урожай: ц/га с функцией принадлежности ,  ц/га с функцией принадлежности ,  ц/га с функцией принадлежности .

Вычислим теперь сумму , используя формулу (4.1):

 (4.4)

Сравнивая правые части выражений (4.3) и (4.4), видим, что каждая из них представляет собой НЧ, причем НЧ (4.3) является собственным подмножеством нечеткого множества (4.4). Иными словами, в нечетком множестве (4.4) по сравнению с (4.3) появились два новых элемента:

 , ,(4.5)

которые по сути дела привносят собой ненужную, более того, отвлекающую информацию о результатах выполнения операции сложения. Действительно, представленные в (4.5) урожайности 35 ц/га со значением ФП  и 65 ц/га со значением ФП  просто непредусмотрены содержательным смыслом рассматриваемой ситуации, определяющей суммарный выход продукции с пахотных угодий площадью 2 га.

Таким образом, каждое из четырех представленных выше известных определений операции суммирования нечетких чисел [13], [32], [64], [76] не позволяет адекватно отразить операцию суммирования нечетких весов, т.е. НЧ в известных теоретико-графовых моделях задач землепользования. Отсюда следует, что применительно к таким конкретным задачам, как упомянутая задача землепользования необходимо представлять новое, более адекватное реальным ситуациям определение операции суммирования двух нечетких чисел.

4.1.2.3. Методы построения нечетких множеств

Теория нечетких множеств позволяет моделировать приближенные рассуждения человека. Основной трудностью, мешающей интенсивному применению теории нечетких множеств при решении практических задач, является то, что функция принадлежности должна быть задана вне самой теории. Существует ряд методов построения по экспертным оценкам функции принадлежности нечеткого множества [19]. Из них можно выделить два основных: прямые и косвенные.

Прямые методы определяются тем, что эксперт непосредственно задает правила нахождения значений функции принадлежности , характеризующей некоторое свойство . Эти значения согласуются с его предпочтениями на универсальном множестве  следующим образом:

1) для любых  выполняется свойство  тогда и только тогда, когда  предпочтительнее , т.е.  в большей степени обладает свойством ;

2) для любых   тогда и только тогда, когда  и  безразличны относительно свойства .

Для получения функции принадлежности нечеткого множества можно использовать следующую процедуру:

a) определить список свойств, по которым оценивается объект;

б) найти в этом списке полярные свойства и сформировать полярную шкалу;

в) для каждой пары полюсов оценить понятие того, как сильно оно обладает положительным свойством.

Исходя из полученной полярной шкалы, эксперт задает степени принадлежности  элементов универсального множества  нечеткому множеству , формируя, таким образом, векторную функцию принадлежности .

Как правило, прямые методы используются для описания понятий, которые характеризуются измеримыми свойствами, такими, как высота, рост, вес, объем. В этом случае является удобным непосредственное задание значений степени принадлежности. Если гарантируется, что люди далеки от случайных ошибок и работают как “надежные и правильные приборы”, то можно спрашивать их непосредственно о значениях принадлежности. Однако из-за возможности искажений (например, субъективная тенденция сдвигать оценки объектов в направлении концов оценочной шкалы) прямые измерения, основанные на непосредственном определении принадлежности, должны использоваться только в том случае, когда такие ошибки незначительны или маловероятны.

На практике бывают случаи, когда не существует элементарных измеримых свойств или признаков, с помощью которых определялись бы интересующие нас понятия, например, эффективность. В таких случаях трудно проранжировать степень проявления некоторого свойства у рассматриваемых элементов. Так как степени принадлежности рассматриваются на конкретном реальном множестве, а не в абсолютном смысле, то интенсивность принадлежности можно определить, исходя из попарных сравнений рассматриваемых элементов. Если значения степени принадлежности были бы известны, например, , , то попарные сравнения можно представить матрицей отношений , . Так как отношения сравнения  в реальном случае неточны из-за того, что они получены эмпирическим способом, необходимо вычислить оценки для . Для получения этих оценок формируется матрица сравнений  рассматриваемого множества элементов. Элементами такой матрицы являются значения, показывающие, во сколько раз один элемент лучше другого. Значения координат собственного вектора матрицы , деленные на их сумму, служат искомыми степенями принадлежности.

При формировании оценок попарных сравнений обычно эксперта просят отразить ощущения или опыт следующим образом:

а) установить, какой из двух предлагаемых элементов, по его мнению, более важен;

б) оценить восприятие интенсивности различия в виде ранга важности по определенной ранговой шкале.

В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформированным условиям. Из числа этих методов [19] заслуживают внимания такие, как использование статистических данных, параметрический подход, а также подход на основе интервальных данных. Косвенные методы более трудоемки, чем прямые, но их преимущество – в стойкости по отношению к искажениям в ответе.

Представленный в [13] анализ многочисленных публикаций, посвященных определению функции принадлежности, убеждает нас в том, что конкретный вид этих функций определяется, в первую очередь, содержательным смыслом исследуемой задачи.