Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

4.2.1. Прогнозирование временных рядов на базе инструментария фазового анализа

Неопределенность данных, выражаемая интервальными или нечеткими числами, является результатом прогнозирования временных рядов (ВР) соответствующих показателей. Одним из инструментарием прогнозирования является фазовый анализ, использование которого можно продемонстрировать на конкретном ВР солнечной активности.

Используемые в настоящем изложении термины, понятия и факты, относящиеся к пятнообразовательной деятельности Солнца, можно найти в[21]. В контексте предпрогнозного анализа и прогнозирования ВР чисел Вольфа (среднемесячных и среднегодичных) можно использовать такой метод нелинейной динамики [54], [86], как инструментарий фазового анализа [47], [71], [73], который позволяет выявлять новые закономерности, не обнаруживаемые с помощью математической статистики.

Временной ряд (среднегодичных) значений чисел Вольфа обозначим через , где индексом  занумерованы годы с 1700 по 2005. В целях визуализации на рис.4.3 дано графическое представление ВР .

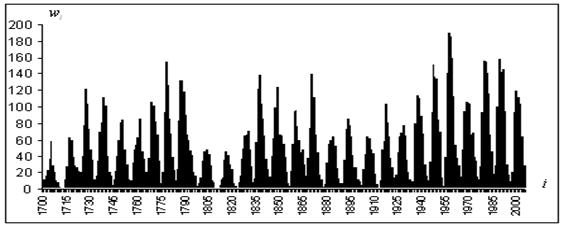
Рисунок 4.3. Графическое представление временного ряда среднегодичной солнечной активности за период 1700-2005 гг.

Предлагаемый инструментарий фазового анализа базируется на построении фазовой траектории , , представленной на рис.4.4(а) где пары соседних точек ,  соединяются отрезком кривой.

Эта фазовая траектория разбивается на фазовые квазициклы , . Число точек в квазицикле  называется его длиной и обозначается через . В качестве типичного на рис.4.4(б) представлен квазицикл , у которого длина , равная 10, означает, что он является 11- летним, т.е. состоит из 11 уровней ВР . Представленная на рис.4.4(а) фазовая траектория ВР  фактически состоит из 28 завершенных квазициклов, которые в совокупности включают в себя 306 (среднегодичных) уровней . Отсюда получаем среднее значение длины квазициклов вида рис.4.4(б):  лет, т.е. оказалось вычисленным среднее значение длительности так называемого «11-летнего цикла» [21].

В таблице 4.1 приведены частости длин квазициклов ВР , откуда вытекает также 11-ти летнее значение средней длины годичных квазициклов; в области значений длин  типичными являются 10 и 11 лет. Отметим, что представленные в табл.4.1 данные в терминологии [21] определены согласно правилам «эпохи минимумов» (эти данные в [21] определяют продолжительность цикла в пределах от 9,0 до 13,6).

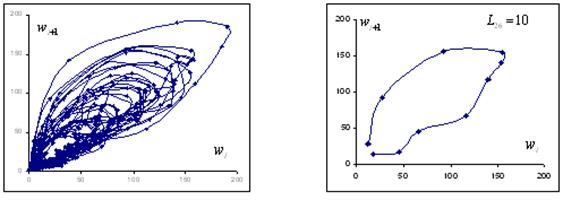
Рисунок 4.4. а) Фазовая траектория временного ряда среднегодичной солнечной активности , б) ее типичный квазицикл  длиной .

 Таблица 4.1. Распределение частостей длин квазициклов временного ряда среднегодичной солнечной активности . 

Остановимся теперь на вопросе (“вероятно существующего” [21]) векового цикла пятнообразования. Представленная в [21] библиография позволяет назвать следующие 3 подхода в попытках различных авторов обосновать существование векового цикла и оценить его продолжительность: 1)метод векового сглаживания (В. Глайзберг, Д. Шов, М. Эйгенсон, М. Вальдмайер), 2)метод скользящих средних (Б. Рубашев, Ю. Витинский), а также использование спектрального анализа и индексов мощности явлений пятнообразования. Различные подходы привели к различным оценкам продолжительности вековых циклов: 79 лет, 80-90 лет и др.

Описанию предлагаемого ниже метода фазовых траекторий предпошлем одно замечание. В [21] отмечено следующее предложение В.Ф. Чистякова: «вековой цикл начинается и заканчивается максимумом». Фазовый анализ выделения векового квазицикла базируется на ВР локальных максимумов , , где  – это значение максимального уровня в -ом квазицикле ВР ,  – число наблюдаемых квазициклов. В табл.4.2 представлен временной ряд , а на рис.4.5 приведена фазовая траектория , .

 Таблица 4.2. Временной ряд  локальных максимумов

 Рисунок 4.5. Фазовая траектория  временного ряда  локальных максимумов

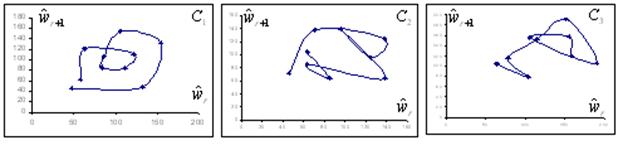
 Рисунок 4.6. Вековые циклы временного ряда среднегодичной солнечной активности .

На рис.4.6(а, б, в) представлено разложение этой фазовой траектории на 3 сложных квазицикла ,  и  (термин «сложный» означает наличие внутри квазицикла петли, происхождение которой объяснил В.Ф. Чистяков: «вековой цикл обычно характеризуется двумя максимумами, которые разделены «провалом»). В терминах нумерации точек фазовой траектории  на рис.4.6 цикл  начинается в точке 6 и заканчивается в точке 105, т.е. его длина  равна  лет; цикл  начинается в точке  и заканчивается в точке , т.е. его длина  равна  года; тогда длина цикла  составляет  лет. Оставляя пока в стороне вопрос о том, является ли завершенным или незавершенным цикл  с учетом значений , , условимся называть вековыми пересекающиеся циклы , ,  (локальные максимумы  и  выполняют двоякую роль – конец одного цикла и начало другого).

Перечислим характерные особенности, которые присущи циклам , , :

- в фазовой траектории  точки начала этих квазициклов сосредоточены в узкой окрестности (на рис.4.5 см. точки с номерами 1, 10, 19);

- каждый из квазициклов длится порядка одного столетия в земных годах;

- в терминах фазовой траектории локальных максимумов  на рис.4.6 структура каждого квазицикла удовлетворяет правилу «восход – петля (упомянутая выше) – нисход»;

- в измерении количества 11-ти летних циклов для вековых ,  и  выполняются соотношения 0,5+8+0,5, где первое (третье) слагаемое означает ветвь спада (роста) начального (конечного) 11-летнего цикла в составе векового цикла.

Из этих четырех особенностей заключительная, возможно, не является обязательной с учетом того, что у третьего векового цикла его длина  земных лет и, кроме того, на рис.4.6(в) точка окончания цикла  находится на значительном расстоянии от точки его начала. Последнее дает некоторые основания предположить, что следующий 11-ти летний цикл ,  окажется достаточно коротким и незначительным по величине локального максимума . В этом случае присоединение этого (пока не существующего) максимума к точке завершения векового квазицикла  на рис.4.6(в) окажется достаточно близкой к точке его начала. При этом в единицах измерения земного года вековой цикл  может оказаться на несколько лет длиннее .

Рассмотрим результаты фазового анализа ВР среднемесячных чисел Вольфа , . В качестве иллюстративного примера рассмотрим период с января 1981 г по декабрь 2005 г., т.е. . Фазовая траектория ВР среднемесячных чисел Вольфа ,  в определенном смысле содержит циклическую компоненту, которая, однако, проявляет принципиальное отличие от циклической компоненты фазовой траектории ВР среднегодичных чисел Вольфа (см. рис.4.4 и табл.4.1). На рис.4.7 дано графическое представление распределения частостей длин квазициклов ВР среднемесячной солнечной активности . Здесь поведение квазициклов длины 3 принципиально отличается от квазициклов длины . По существу в случае  соответствующие части фазовой траектории не являются квазициклами, а представляют лишь последовательности ацикличных отрезков, т.е. зигзагообразных отрезков фазовой траектории. Эти ацикличные отрезки появляются в окрестности смены знака приращений («+» на «-» или «-» на «+») среднегодичного ВР  (см. рис.4.3), т.е. в окрестности локальных точек максимума (или минимума) этого ВР. Собственно «циклическая часть» фазовой траектории  состоит из квазициклов, которые имеют в среднем полугодичную длительность.

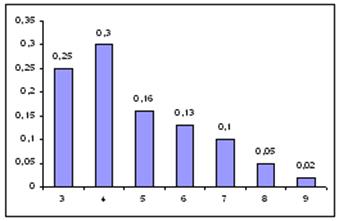
 Рисунок 4.7. Распределение частостей длин квазициклов временного ряда среднемесячной солнечной активности .

 Резюмируя результаты фазового анализа ВР солнечной активности, можем отметить их определенную согласованность с общепризнанными фактами [21] в той части, которая касается 11-ти летних циклов среднегодичного ВР солнечной активности. В то же время по отношению к уже известным результатам более ранних исследований [21] существует определенное расхождение в той части, которая касается вековых циклов (мы получили существенно более определенные оценки числовых значений параметра их длины), а также квазициклов среднемесячного ВР солнечной активности. Заслуживает внимания также тот факт, что фазовый анализ ВР солнечной активности устанавливает трехуровневую иерархию в структуре динамики эволюционирования уровней солнечной активности. Нижний уровень этой иерархии составляют квазициклы среднемесячного ВР, средний уровень составляют 11-ти летние квазициклы среднегодичного ВР чисел Вольфа, верхний уровень составляют вековые циклы. Можно говорить о сравнительном анализе трех рассматриваемых ВР , ,  по такому показателю, как качество цикличности, т.е. речь идет о степени проявления в этих ВР таких характеристик цикличности (циклической компоненты), как наличие циклов, степень их завершенности и периодичности, отсутствия, или наоборот, наличие джокера [15], [73] и степень его проявления и т.д. С очевидностью можно утверждать, что по “качеству цикличности” наилучшим является ВР среднегодичной солнечной активности , наихудшим – ВР вековых циклов; промежуточное положение занимает ВР среднемесячной солнечной активности . Более подробный анализ вышеуказанных трех иерархических уровней оперирует такими параметрами, как траектория дрейфа центров квазициклов, траектория размера периметров их габаритных прямоугольников и др. [73]. Эти параметры представляют собой исходные данные для прогнозирования уровней ВР солнечной активности.

Выявленная трехуровневая иерархия ВР  солнечной активности представляет предпрогнозную информацию для трех горизонтов прогнозирования: краткосрочного (помесячного), среднесрочного (по годам) и долгосрочного (по десятилетиям). Вышеуказанная предпрогнозная информация представляет возможность разрабатывать достаточно точную и надежную гибридную [99] прогнозную модель вида клеточный автомат + фазовый анализ + нечеткие системы.