Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

4.2.3. Гибридные модели прогнозирования

В настоящее время можно говорить о возрастающем внимании к использованию гибридного подхода [23], [99] к построению интеллектуальных систем, вызванная его высокой эффективностью. Инструментальной базой этого подхода являются так называемые «мягкие вычисления». Напомним, что термин «мягкие вычисления» был введен Л.Заде [10], [31] и, как известно, интерпретируется следующей формулой: Мягкие вычисления = нечеткие системы + нейронные сети +генетические алгоритмы. В настоящей работе слагаемые этой формулы изменены следующим образом: вместо«нейронной сети» используется «клеточный автомат», а вместо «генетического алгоритма», осуществляющего оптимизационную настройку функций принадлежности нечетких множеств [99], используется «фазовый анализ».

Реализацию идеи прогнозирования с помощью предлагаемого «тройного гибрида» продемонстрируем, используя представленные в предыдущем п.4.2.2 ВР заболеваемости  и . Фазовые траектории рассматриваемых ВР  и  строятся в фазовом пространстве размерности 2 и представляются множествами (координат) точек соответственно ,  и , , где каждая пара точек соединяется кривой. На рис.4.8 представлен 8- недельный базовый отрезок фазовой траектории . На рис.4.9 представлен годовой базовый отрезок фазовой траектории . Эти отрезки выполняют роль «обучающих выборок» [99].

Согласно определению клеточно-автоматной прогнозной модели [71] прогнозируемое значение  очередного уровня рассматриваемого ВР  представляется в виде двух нечетких множеств (НМ): лингвистического НМ  и числового НМ , где ,  и  – это термы, представляющие такие значения лингвистических переменных, как «низкое», «среднее» и «высокое» значение  уровня заболеваемости;   и  – значения функции принадлежности для этих уровней заболеваемости. Аналогично для ВР  результат клеточно-автоматного прогнозирования очередного уровня  представляется двумя НМ:  , и   В процессе гибридного прогнозирования корректируются значения функции принадлежности ,  и  в зависимости от того, в какую «зону» (,  или ) попадают вычисленные прогнозные значения этой функции при сравнении их с обучающей выборкой.

Валидация, т.е. оценка погрешности «негибридного» клеточно-автоматного прогнозирования ВР  осуществлялась для 8- недельного горизонта прогноза, , , ; погрешность прогноза в худшем случае не превосходила 16 %. Аналогично, валидация клеточно-автоматного прогнозирования ВР  осуществлялась для 12- месячного горизонта прогноза, , , , погрешность прогноза не превосходила 20 %. Т.е. отрезки ,  и ,  вместе со “своими” отрезками фазовых траекторий вида рис.4.9 и рис.4.10 представляют собой обучающую выборку, т.е. базу для дополнительного входа [99] позволяющего настроить («оптимизировать») в режиме обучения функцию принадлежности  выходных (т.е. прогнозируемых) переменных для вышеуказанных горизонтов прогноза. Погрешность гибридного прогнозирования уменьшилась в ~ 2 раза по сравнению с вышеупомянутой погрешностью «чисто» клеточно-автоматного прогнозирования.

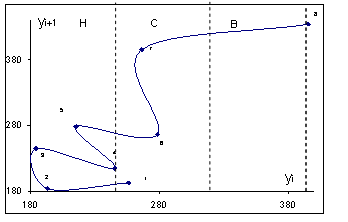
 Рисунок 4.10.  Базовый квазицикл для «обучения» функции принадлежности  применительно к временному ряду .

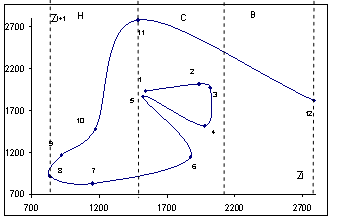
 Рисунок 4.11. Базовый квазицикл для «обучения» функции принадлежности применительно к временному ряду .

 Полученный результат гибридного прогнозирования: в худшем случае ошибка прогнозирования не превышает 10% как для ВР , так и для ВР .