Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

5.6. Асимптотически точный алгоритм

В настоящем параграфе предлагается приближенный алгоритм с оценкой, получающий асимптотически оптимальное решение. Через  обозначим множество всех полных - вершинных графов , у которых каждому ребру  приписан вес , представляющий собой интервал из множества интервалов

 , , ,

т.е. для ребра  его вес

 , , .(5.22)

При заданном параметре  допустимым решением рассматриваемой задачи покрытия графа  звездами является всякий такой его остовный подграф , , в котором каждая компонента связности представляет собой -вершинную звезду;  – множество всех допустимых решений (МДР).

На МДР  определена максимизируемая ИЦФ

 ,(5.23)

где при вычислении интервально-значной функции  осуществляется классическое суммирование [11] интервалов :

 ,

где

 , .(5.24)

В работе [7] обосновывается утверждение о том, что всякая интервальная задача на графах с ИЦФ (5.2) эквивалентна соответствующей производной от нее 2-критериалыюй задаче с векторной целевой функцией (ВЦФ)

 ,(5.25)

состоящей из двух критериев весового вида MAXSUM

 , ,(5.26)

где  и ,  – пара весов, которой взвешены ребра  полного графа , при условии , , т.е. значения критериев (5.24) и (5.26) совпадают.

ВЦФ (5.25)-(5.26) в МДР  определяет ПМ  [74]. Искомым решением рассматриваемой 2-критериальной задачи покрытия графа  - вершинными звездами является ПМА .

Примечание 5.1. Среди методов отыскания паретовских оптимумов (ПО)  многокритериальных задач наиболее распространенными являются алгоритмы линейной свертки критериев (АЛСК) [74]. Эти алгоритмы базируются на том факте, что при положительно определенной -критериальной ВЦФ элемент , максимизирующий (минимизирующий) линейную свертку критериев (ЛСК)

 ,(5.27)

является ПО [74]. Здесь вектор , где

.

Рассмотрим некоторую индивидуальную задачу с  максимизируемыми критериями, которые определены на МДР . Если для каждого ПО  найдется вектор , удовлетворяющий равенству , то говорят, что проблема нахождения ПМА  разрешима с помощью АЛСК. Если определенная таким образом разрешимость присуща всем индивидуальным задачам рассматриваемой массовой задачи, то для каждой из них можно найти искомое ПМА с помощью АЛСК.

Примечание 5.2. В однокритериальной классической постановке задача покрытия графа звездами является NP- трудной [27], откуда вытекает, что к настоящему времени отсутствуют полиномиальные алгоритмы ее решения. В многокритериальной [89] или интервальной постановке [11] она является труднорешаемой. Последнее означает, что нижняя оценка вычислительной сложности нахождения ее ПМА растет экспоненциально от размерности .

В настоящей главе для интервальной задачи покрытия графа звездами предлагается полиномиальный двухуровневый АЛСК нахождения допустимого решения, которое в определенном смысле близко к искомому оптимуму.

На нижнем уровне каждому ребру присваивается значение линейной свертки значений границ его весового интервала, а на верхнем уровне находится допустимое решение с помощью предлагаемого градиентного алгоритма . Для построения ЛСК вида (5.27) вначале выбирается конечное подмножество  множества . Далее для каждого вектора  строится JICK

 .(5.28)

В силу аддитивной природы критериев (5.26) ЛСК (5.28) представляем в качестве целевой функции (ЦФ) оптимизационной задачи, решаемой на верхнем уровне:

 .(5.29)

Из примечания 5.1 следует, что решение, оптимальное по ЦФ (8), является парето-оптимальным по ИЦФ (5.23)-(5.24) или ВЦФ (5.25)-(5.26). В результате объединения найденных решений по всевозможным вариантам ,  получаем некоторое подмножество паретовского множества . В свою очередь из этого подмножества выделяется некоторое подмножество искомого ПМА . Последнее подмножество можно рассматривать в качестве аппроксимации искомого ПМА .

Описание алгоритма верхнего уровня  для фиксированного вектора . Предлагаемый алгоритм  использует процедуру координатного подъема. Представляемая на вход этого алгоритма исходная информация получается из данного интервально взвешенного полного графа , в котором каждому ребру приписан интервальный вес . В графе  интервальные веса  заменяются на линейную свертку (JIC) их концов

 , ;(5.30)

через  обозначим данный граф , в котором интервальные веса заменены на их свертки вида (5.30).

Работа алгоритма  состоит из 2 этапов  и . Пусть . На этапе  1-взвешенный граф  разбивается произвольным образом на подграфы  с равномощными множествами вершин , . Множество  рассматривается в качестве множества центров звезд.

Этап  состоит из  подэтапов , . На вход подэтапа  представляется двудольный граф , определяемый подмножеством ребер , состоящим из всех таких ребер , что , а . Каждый из подэтапов ,  состоит из шагов ; через , ,  обозначим ребро, выделенное на шаге ;  – множество ребер, выделенное на первых  шагах;  –подмножество вершин , каждая из которых инцидента некоторому ребру . Если , то на шаге  выделяется такое ребро , , которое инцидентно вершине  и при этом его ЛС  имеет максимальное значение среди таких ребер , каждое из которых не пересекается с каким-либо ребром :

 ,(5.31)

где .

Далее ребро  окрашивается, после чего осуществляется реализация следующего шага. По завершению шага  подэтап  завершает свою работу и далее следует переход к подэтапу , . На шаге  завершает свою pa6oту подэтап , а вместе с ним и этап .После этого случае в каждом из двудольных графов ,  выделяем множество  всех окрашенных ребер , составляющих совершенное паросочетание в , после чего в данном графе  выделяем -дольный остовный подграф , где . Т.к. алгоритм  применен к полному графу, то по определению этапа  окрашенные ребра, инцидентные вершине ,  образуют -вершинную звезду, т.е. подграф  представляет собой допустимое решение ,  рассматриваемой задачи на полном 1-взвешенном графе , .

Определим, каким условиям должны удовлетворять параметры задачи (5.23)-(5.24) для того, чтобы получаемое решение было асимптотически оптимальным по ЛСК (5.29). Для этого воспользуемся техникой вероятностного анализа комбинаторных алгоритмов [66].

Асимптотическую точность алгоритма  будем обосновывать, используя аппарат теории случайных (вероятностных) графов [12], [44].

Через  обозначим полный вероятностный - вершинный граф, в котором для какой-либо пары вершин  ребру  с условной вероятностью  присваивается определенный согласно (5.22) интервальный вес , , . Применив к  алгоритм нижнего уровня, каждому его ребру с согласно (5.30) присвоим значение ЛС. Взвешенный таким образом граф  обозначим через .

Через  обозначим множество всех -вершинных графов , у которых при фиксированном  каждому ребру  приписано значение ЛС (5.30). Последовательности  будем ставить во взаимнооднозначное соответствие последовательность множеств  и последовательность чисел , , а также последовательность вероятностных графов .

Через  будем обозначать допустимое решение, которое получено в результате применения алгоритма  к графу ,значение ЦФ (5.29) для этого решения .

Через  будем обозначать вес оптимального по ЦФ  решения рассматриваемой задачи на данном графе .

Определение 5.9. Пусть существует последовательность , , , для которой свойство  выполняется для почти всех графов  или выполняется с вероятностью ,  для графа . Тогда будем говорить, что  почти всегда приводит к асимптотически точному решению. При этом удовлетворяющее этому определению допустимое решение будем называть асимптотически точным [25], [66].

При фиксированном  по аналогии с (5.30) применим к элементам  операцию преобразования их в ЛС

 , .(5.32)

Обозначим через  упорядоченное по возрастанию множество , .

Всякий полный - вершинный 1-взвешенный граф, ребрам  которого приписаны веса  из множества , по определению принадлежит определенному выше множеству , которое в дальнейшем обозначим через .

Через  будем обозначать вероятностный -вершинный полный граф, в котором всякому его ребру  приписывается вес ЛС  с вероятностью  согласно распределению вероятностей

 , , , , ,(5.33)

где  – интегральная функция распределения, .

Необходимо обосновать накладываемые на множество  вероятностные условия, при выполнении которых алгоритм  почти всегда приводит к асимптотически точному решению.

Пусть к некоторой реализации вероятностного -вершинного графа  применен алгоритм , в результате чего получено допустимое решение , на котором ЦФ (5.29) принимает значение . Через  будем обозначать нижнюю оценку значения некоторой ЦФ на оптимальном покрытии  рассматриваемой реализации графа . Пусть для величин  выполняется указанное выше распределение вероятностей (5.33). Определим условия, при выполнении которых вероятность получения асимптотически точного решения стремится к 1:

 ,(5.34)

где  и  при .

Согласно равенства  число ребер, составляющих остовные подграфы  и , определяется соотношением

 .(5.35)

Далее с учетом определения величин  и  согласно (5.35) получаем неравенство , откуда для выполнения неравенства (5.34) достаточно, чтобы выполнялось следующее соотношение:

 .(5.36)

Пусть  – математическое ожидание величины ,  – дисперсия величины . Допустим, что мы получили нижнюю оценку  для математического ожидания : . Выберем новую величину  так, что выполняется строгое неравенство  и оценим вероятность того, что величина  не превосходит . Воспользуемся неравенством Чебышева:

 .(5.37)

Величину  определим следующим образом:

 ,(5.38)

где  – произвольная, сколь угодно медленно растущая функция,  с ростом . Тогда

 .(5.39)

Перейдем теперь к вычислению нижней оценки матожидания . Учитывая обозначения, использованные при описании этапа , рассмотрим работу его первого подэтапа , состоящего из шагов . На каждом шаге выбирается ребро максимального веса из множества, мощность которого обозначим через : , . Значения этого максимума обозначим через ;  – математическое ожидание величины выделяемого максимума .

Через  обозначим суммарный вес ребер, выделенных и окрашенных в двудольном подграфе  графа  в процессе работы подэтапа , ;  – математическое ожидание величины .

В принятых обозначениях результатом работы шага  подэтапа  является выделенное на этом шаге ребро , вес которого равен . Математическое ожидание  можно вычислить по формуле

 ,(5.40)

где

 .(5.41)

По определению графа  вычисляемые согласно (5.26) элементы  независимы. Отсюда с учетом соотношения  и равенств (5.30), (5.31), а также известной формулы для вычисления суммы бесконечной убывающей геометрической прогрессии, вычисляем матожидание :

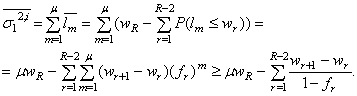
По определению алгоритма  выделяемые им множества ребер ,  попарно не пересекаются, а по определению графа  веса ребер этого графа являются независимыми случайными величинами. Поэтому математическое ожидание веса покрытия  представляет собой сумму математических ожиданий результатов работы подэтапов , :

 .(5.42)

Учитывая, что правая часть выражения (5.42) не зависит от значения индекса , получим оценку, для представленной выше величины :

 .(5.43)

На основании (5.28) и (5.43) вычисляем значение :

.

Последнее выражение для расчета  можем преобразовать в терминах ЛС (5.20):

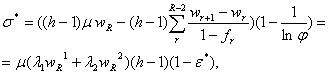 (5.44)

где .

С учетом (5.24) и упорядочения элементов  для оптимального значения  справедлива верхняя оценка . Тогда на основании полученной формулы (5.44) для оценки  можем сформулировать следующее

Утверждение 5.5. Для того, чтобы имело место стремление  при  достаточно, чтобы выполнялись неравенства

.

Аналогично вычислим верхнюю оценку для дисперсии :

 .(5.45)

Подставляя (5.43)и (5.45) в (5.29) с учетом равенства  можем записать:

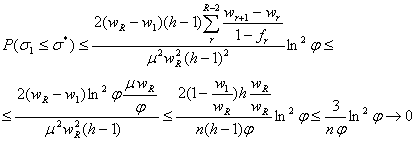
при .

Отсюда с учетом утверждения 5.2 доказана следующая

Теорема 5.6. Если распределение вероятностей (5.43) для весов ребер графа  удовлетворяет неравенству

,

то с вероятностью ,  при  решение , полученное с помощью алгоритма , является асимптотически точным. При этом вычислительная сложность этого алгоритма .

Последнее утверждение теоремы 5.6 очевидно, т.к. согласно своему определению, каждое ребро данного графа алгоритм  просматривает не более одного раза, в силу чего , где .

В целях сравнения полученных в настоящей главе результатов с известными ранее [25], [66] рассмотрим частный случай расположения интервалов на числовой оси. Пусть интервалы ,  имеют длину, равную 2. Центры интервалов представляют собой возрастающую последовательность целых чисел с шагом 1, правые и левые границы интервалов являются целыми числами. Распределение вероятностей является равновероятным, т.е.  и для всякого . В этом случае справедливо следующее

Утверждение 5.6. Для почти всех графов  решение  является асимптотически точным, если выполняется неравенство .

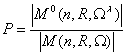Доказательство. Действительно, пусть  обозначает множество всех графов , для каждого из которых в контексте определения 5.9 справедливо неравенство , . Это неравенство равносильно тому, что в случае равномерного распределения вероятность  получения асимптотически точного решения  равна отношению . Поэтому достаточно показать, что при выполнении условий этого утверждения для равномерного распределения имеют место равенства , , где величины ,  определяются выражениями (5.29), (5.34) в контексте определения 5.9. Из них вытекает следующее обоснование асимптотической точности решения , получаемого на выходе алгоритма :

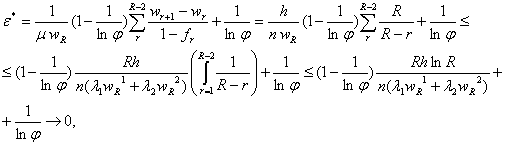
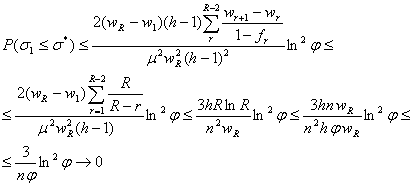
при  и

 , .(5.46)

Утверждение 5.6 доказано.

Среди известных результатов о достаточных условиях асимптотической точности градиентных алгоритмов можно привести следующий [25], [66]. Если множество  и  для почти всех графов  алгоритм градиентного типа находит асимптотически точное решение задачи коммивояжера с минимизируемой ЦФ. Отметим, что при таком определении  достаточное условие утверждения 5.6 принимает вид (5.36). Т.о., область достаточных условий асимтотической точности в случае максимизируемой ЦФ экспоненциально превосходит область достаточных условий асимптотической точности минимизируемых критериев [66].

В работе [53] для максимизируемой ЦФ получены достаточные условия асимптотической точности алгоритма координатного подъема для задачи о цепях в виде . Таким образом, представленные в утверждении 5.6 достаточные условия асимптотической точности градиентного алгоритма для задачи с интервальными данными фактически совпадают с достаточными условиями асимптотической точности аналогичного алгоритма для задачи с детерминированными данными в случае, когда параметр  является константой или ограниченной растущей функцией от .

Полученные в настоящей книге результаты относятся к классу задач дискретного программирования в условиях неопределенности данных. Исследуемая авторами проблема оценки эффективности градиентных алгоритмов для экстремальных задач на интервально взвешенном графе, по-видимому, ранее рассмотренной не была. Представленная выше теорема 5.6 устанавливает принципиальную возможность обоснования асимптотической точности алгоритмов градиентного подъема (спуска) для дискретных задач с интервальными данными. Представляет интерес исследование других задач дискретной оптимизации с интервальными данными.