Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Основы проектирования гидротехнических сооружений, лесных бирж и рейдов приплава

Седрисев Д Н, Рубинская А В, Аксёнов Н В, Кожевников А К,

7.4. Расчет элементов бетонных и железобетонных конструкций по предельным состояниям первой группы

Расчет по прочности бетонных элементов. Производится расчет для сечений, нормальных к продольной оси. В зависимости от условий работы элементов они рассчитываются без учета, а также с учетом сопротивления бетона растянутой зоны.

Без учета сопротивления бетона растянутой зоны рассматриваются внецентренно сжатые элементы, в которых по условиям эксплуатации допускается образование трещин (элементы, не подверженные действию агрессивной воды и не воспринимающие напор воды). Предельное состояние таких элементов характеризуется разрушением бетона сжатой зоны при достижении напряжений, равных призменной
прочности бетона Rb. Эпюра напряжений в сжатой зоне условно принимается равномерно распределенной (рис. 7.6, а).  

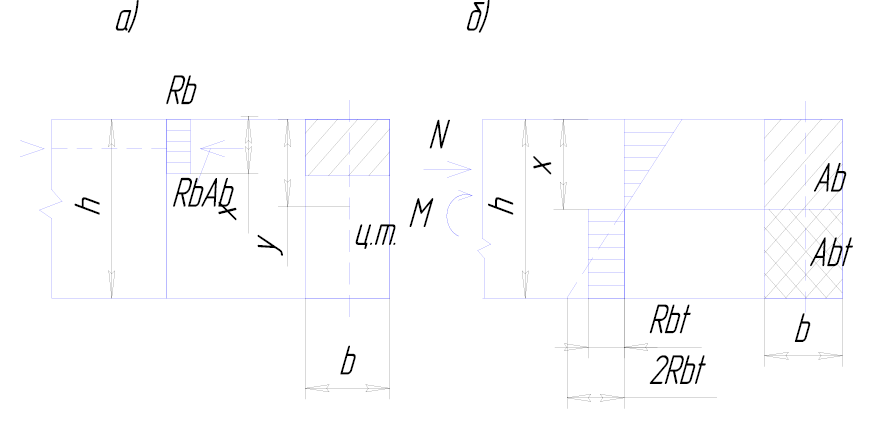
Рис. 7.6. Схема усилий и эпюра напряжений в сечении, нормальном
к продольной оси бетонного элемента:
а – внецентренно сжатого, рассчитываемого по прочности без учета сопротивления бетона растянутой зоны; б – изгибаемого (внецентренно сжатого), рассчитываемого по прочности с учетом сопротивления бетона растянутой зоны: Ц. Т. – центр тяжести сечения

Расчет прочности таких элементов производится так:

уп yf ylc уса N ≤ φ уbi Rb Ab, (7.22)

С учетом сопротивления бетона растянутой зоны сечения рассчитываются все изгибаемые элементы, а также внецентренно сжатые элементы, в которых по условиям эксплуатации образование трещин не допускается. При этом принимается, что достижение предельного состояния характеризуется разрушением бетона рас тянутой зоны (появлением трещин). Напряжения в бетоне растянутой зоны принимаются равномерно распределенными и равными Rbt (рис. 7.6, б).

Таблица 7.3

Коэффициент продольного изгиба

Примечания:

1. Наименьший размер прямоугольного сечения b.

2. Наименьший радиус инерции сечения i.

Расчетная длина элемента lef, принимаемая в зависимости от характера закрепления концов элемента равной: при полном защемлении обоих концов 0,5l; при полном защемлении одного конца и шарнирно неподвижном закреплении другого 0,7l; при шарнирно неподвижном закреплении обоих концов l;при одном полностью защемленном и одном свободном конце 2l; l – геометрическая длина элемента.

Расчет прочности изгибаемых бетонных элементов производится из условия

уп yf ylc уса M ≤ уbi уh Rbt Apl, (7.23)

Для элементов прямоугольного сечения Wpi = (bh2)/3,5.

Расчет по прочности сечений железобетонных элементов, нормальных к продольной оси. Бетонная балка, лежащая на двух опорах и подверженная поперечному изгибу, имеет малую несущую способность. Несущая способность такой балки ограничивается низким сопротивлением бетона растяжению, в то время как высокое сопротивление бетона сжатию остается неиспользованным (рис. 7.7, а).

Железобетонная балка, в которой растягивающие усилия воспринимаются расположенной внизу арматурой, может иметь несущую способность, почти в 20 раз большую, чем несущая способность бетонной балки таких же размеров без арматуры.

Опытами установлено, что разрушение железобетонной балки, подверженной поперечному изгибу, может произойти или в зоне действия максимальных изгибающих моментов по нормальному к продольной оси сечению Б–Б, или в зоне действия максимальных поперечных сил по наклонному сечению В–В (рис. 7.7, б).  

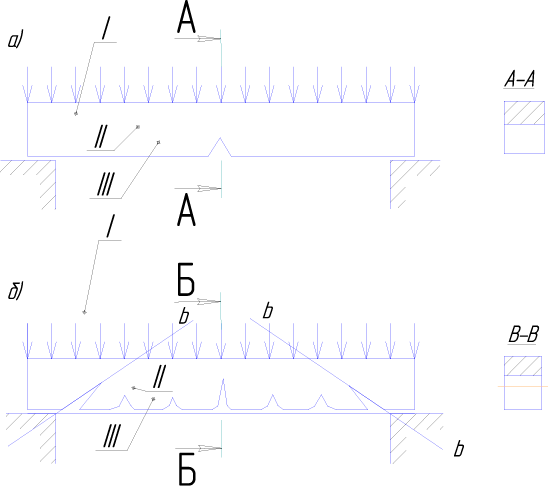
Рис. 7.7. Характер образования трещин
и расчетные сечения в бетонной (а) и железобетонной (б) балках:
/ – сжатая зона; // – нейтральный слой; /// – растянутая зона

Поэтому расчет на прочность железобетонных элементов должен производиться для сечений, нормальных к их продольной оси, а также для наклонных к ней сечений.

Различают две возможные схемы разрушения железобетонного изгибаемого элемента:

1) в рационально армированных изгибаемых элементах разрушение начинается с растянутой арматуры при достижении в ней расчетных сопротивлений Rs

2) в так называемых переармированных элементах разрушение начинается со сжатой зоны бетона при достижении в ней расчетного сопротивления Rbh. При этом напряжения в растянутой арматуре меньше расчетного сопротивления RS, что экономически невыгодно.

При расчетах прочности железобетонных изгибаемых элементов изгибающий момент от внешней нагрузки не должен превышать несущей способности сечения, т.е. М < Мsес.

Для определения внутренних усилий применяют метод сечений. Для этого мысленно разрезают элемент на две части. Одну из них (обычно правую) отбрасывают, а для соблюдения равновесия заменяют действие отброшенной части на оставшуюся внутренними усилиями. Таким образом получают расчетную схему. Затем используют три уравнения статики: сумма моментов всех сил относительно любой точки, сумма проекций усилий на поперечную ось Y и на про дольную ось X должны равняться нулю: ΣМ = 0; ΣХ = 0 ΣY = 0.

Путем решения этих уравнений определяются внутренние усилия, выводятся расчетные формулы.

Расчет прочности изгибаемого железобетонного элемента любой симметричной формы. Расчет производится из условия

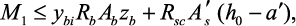(7.24)