Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Выглаживание: качество, технологии и инструменты

Губанов В Ф,

1.1. Процесс выглаживания и его стабильность

Выглаживание, как известно, представляет собой метод отделочно-упрочняющей обработки деталей поверхностным пластическим деформированием, который заключается в деформировании обрабатываемой поверхности скользящим по ней индентором. В результате прикладываемого давления происходит упрочнение поверхностных слоев и образование благоприятного, с позиции износостойкости, микрорельефа поверхности, в частности, сглаженного профиля шероховатости поверхности.

Самыми распространенными способами выглаживания являются: выглаживание с упругим и с жестким закреплением индентора.

Выглаживание с жестким закреплением индентора (рис. 1.1) [53], которое рассматривается в данной работе, осуществляет жесткую кинематическую связь между индентором и обрабатываемой деталью. За счет определенной величины внедрения рабочей части индентора в обрабатываемую заготовку (натяга), реализуется требуемое силовое воздействие рабочей части инструмента на обрабатываемую поверхность, приводящее к пластическому течению материала детали. При этом повышается точность размеров и исправляются погрешности формы (волнистость). Жесткая кинематическая связь позволяет также осуществлять обработку прерывистых поверхностей и применяется на станках повышенной точности.

В результате осуществления процесса выглаживания значительно уменьшаются высотные параметры шероховатости поверхности и повышается ее микротвердость, что, как показывают результаты многочисленных исследований советских и российских ученых, оказывает определяющее влияние на многие эксплуатационные свойства деталей и их соединений. В данной работе при проведении экспериментальных исследований акцент сделан на незакаленные стали, поскольку процесс формирования и обеспечения параметров качества поверхностного слоя «мягких» материалов изучен в меньшей степени, поэтому в ряде случаев возможно из технологического цикла исключить их термообработку, заменив ее выглаживанием.

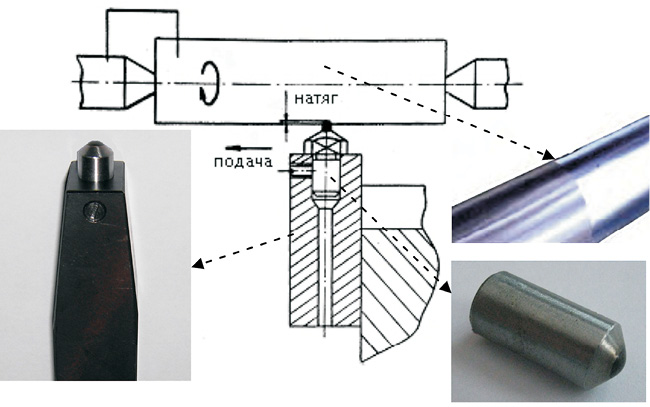
Рис. 1.1. Схема выглаживания с жестким закреплением индентора

На формирование параметров качества поверхностного слоя деталей при выглаживании большое влияние оказывают возникающие в ходе этого процесса автоколебания [33, 53].

При жестком выглаживании для уменьшения интенсивности автоколебаний можно рекомендовать следующее: уменьшить подачу; для сглаживающего режима обработки – увеличить натяг, для сглаживающе-упрочняющего режима обработки – уменьшить натяг; уменьшить скорость выглаживания [10]. Эти мероприятия приведут к уменьшению высотных параметров шероховатости поверхности и будут способствовать образованию регулярной шероховатости поверхности (при условии регулярности исходной шероховатости).

Однако, приведенные рекомендации по уменьшению интенсивности радиальных автоколебаний необходимо использовать рационально, учитывая: трудоемкость обработки, требования к качеству обработанной поверхности, стойкость рабочей части индентора.

Установлено, что свойства вибросигналов из зоны выглаживания косвенно характеризуют стабильность процесса в целом, с точки зрения не только автоколебаний, но и формирования параметров качества поверхностного слоя детали, например микротвердости.

Сила, как известно, связана с ускорением, поэтому, если виброускорение обладает свойством стационарности и эргодичности, сила выглаживания также обладает этим свойством, а, следовательно, и процесс выглаживания – стационарен и эргодичен.

Обеспечение заданных параметров шероховатости возможно только при условии стационарного и эргодичного процесса, что также является одним из условий для обеспечения регулярного профиля шероховатости поверхности.

Можно использовать следующую последовательность действий для проверки стационарности стохастического процесса (вибросигнала) с одновременной проверкой воспроизводимости результатов:

1. Ансамбль разделяется на N равных интервалов (реализаций), причем наблюдения в различных интервалах полагаются независимыми [6].

2. Для каждого интервала проводится серия параллельных опытов при одинаковых условиях обработки, в каждом параллельном опыте определяется среднее значение (m_x) и дисперсия (D_x) вибросигнала.

3. Вычисляются оценки среднего значения m_mx, m_Dx и дисперсии D_mx и D_Dx в каждом интервале для средних значений и дисперсий по результатам параллельных опытов.

Случайный стационарный процесс будет характеризоваться стабильным средним значением и стабильной дисперсией для средних значений и дисперсий, на всех интервалах.

Разобьем ансамбль на 3 равных интервала (в каждом интервале обрабатывается некоторая длина заготовки – одна из базовых длин при измерении параметров шероховатости). Необходимо заметить, что длительность интервалов по времени должна быть больше, чем период самой низкочастотной составляющей сигнала, иначе стационарный процесс может быть ошибочно принят за нестационарный процесс, содержащий нелинейный тренд [7].

Полученные данные (проведем дублирование опытов, n параллельных опытов для каждого интервала, обычно 5 или 6):

1 интервал – (m_mx1, D_mx1) и (m_Dx1, D_Dx1);

2 интервал – (m_mx2, D_mx2) и (m_Dx2, D_Dx2);

3 интервал – (m_mx3, D_mx3) и (m_Dx3, D_Dx3).

Проверка однородности дисперсий по критерию Кохрена (для среднего значения, затем для дисперсии) [5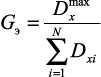1]:

(1.1)

т.е. берется отношение максимальной дисперсии какого-то интервала, по результатам параллельных экспериментов, к сумме дисперсий интервалов.

Если экспериментальное значение критерия Кохрена не превышает табличного (при числе дисперсий, равном числу интервалов N и числе степеней свободы, равном f = n – 1), значит, дисперсии однородны.

Для определения равенства оценок математического ожидания (для среднего значения, затем для дисперсии) используется расчетный критерий максимального относительного отклонения (для максимального и минимального значения математического ожидания в интервале с наибольшей дисперсией, в случае необходимости – для всех интервалов) [51]:

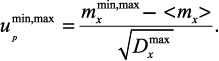(1.2)

Если расчетные значения критерия максимального относительного отклонения по абсолютной величине меньше табличного значения, гипотеза равенства оценок математического ожидания принимается, т.е. одновременно со стационарностью проверяется идентичность вибросигналов при воспроизведении одних и тех же условий обработки.

Для того чтобы вибросигналы были эргодичными, необходимо, чтобы ковариационные функции интервалов были одинаковы (в случае нормального распределения) [7]. Иначе говоря, случайный процесс строго эргодичен, если с вероятностью, равной единице, его статистические характеристики можно предсказать по одной реализации (интервалу) из ансамбля с помощью усреднения по времени [6].

Анализ вибросигналов, записанных при различных (стабильных) условиях жесткого выглаживания, позволяет сделать вывод о том, что вибросигналы являются стационарными и эргодичными.

Рассмотрим теперь изменение вибросигнала во времени, с точки зрения его частотного наполнения. Если процесс обработки стабилен, в спектре вибросигнала в различные моменты времени присутствует один и тот же набор частот. Появление или исчезновение какой-нибудь частоты свидетельствует о появлении экстренной ситуации (например, катастрофический износ инструмента, раковина на поверхности заготовки и т.д.).

На рис. 1.2 представлен пример частотно-временного представления вибросигнала при выглаживании. Очевидно, что процесс обработки стабилен (т.к. в спектре вибросигнала присутствует один и тот же набор частот).

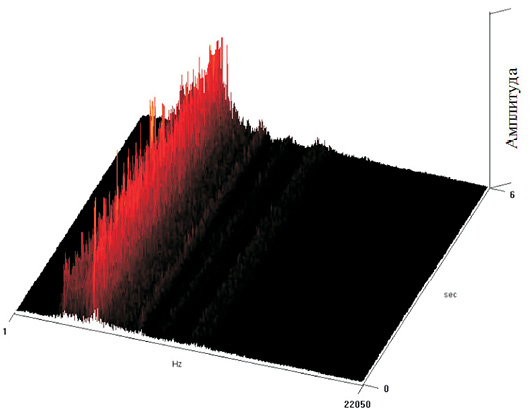
Рис. 1.2. Частотно-временное представление вибросигнала
при выглаживании