Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Выглаживание: качество, технологии и инструменты

Губанов В Ф,

1.2. Шероховатость поверхностей выглаженных деталей

Известно [51], что из параметров шероховатости рабочих поверхностей деталей такие параметры, как Ra – среднее арифметическое отклонение профиля, мкм, Sm – средний шаг неровностей профиля, мм, S – средний шаг местных выступов профиля, мм, Rp – высота сглаживания профиля шероховатости, tp – относительная опорная длина профиля на уровне p, Rmax – наибольшая высота профиля, оказывают наибольшее влияние на различные эксплуатационные свойства деталей. Обеспечение заданных значений параметров шероховатости поверхности является целью почти всех методов механической обработки деталей. При этом, в качестве непараметрической оценки неровностей используются профилограммы, коррелограммы (рис. 1.3), гистограммы и спектрограммы (рис. 1.4) всей поверхности, а в качестве параметрической – параметры этих кривых [50].  

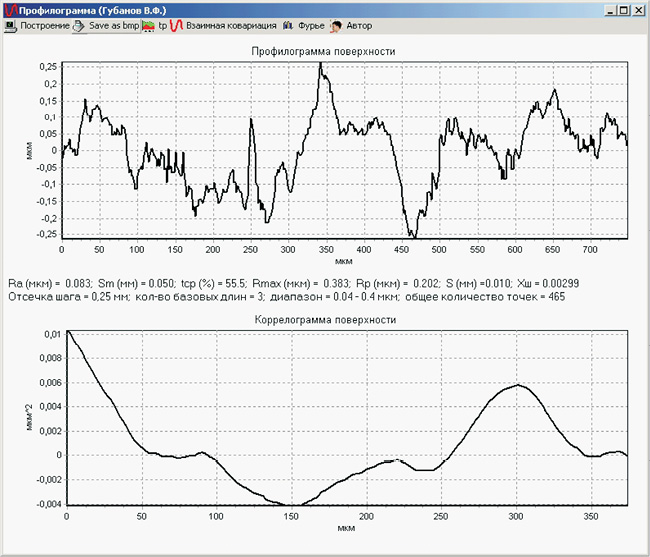
Рис. 1.3. Пример профилограммы и коррелограммы
выглаженной поверхности

Шероховатость выглаженной поверхности обычно имеет благоприятную «притупленную» форму (рис. 1.5), что наряду с повышенной микротвердостью поверхности и значительными сжимающими остаточными напряжениями повышает износостойкость деталей, работающих в условиях трения.

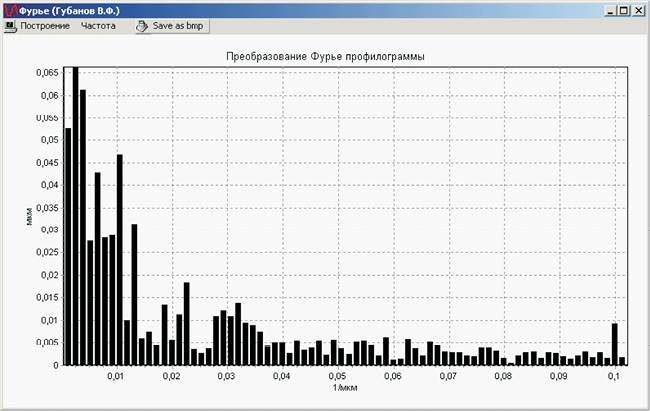
Рис. 1.4. Пример спектрограммы выглаженной поверхности

Проведенные исследования профилограмм выглаженных поверхностей показывают, что обеспечение заданного значения Ra (табл. 1.1: «+» – указывает на наличие корреляционной связи, «–» – указывает на отсутствие корреляционной связи) автоматически приводит к получению заданных значений Rmax и Rp. Это означает также, что обеспечение заданного значения Ra автоматически не обеспечит, в большинстве случаев, такие важнейшие составляющие профиля как Sm, tp, S.

Учитывая вышесказанное, необходимо искать определенный диапазон условий обработки, в котором гарантированно бы обеспечивались заданные значения параметров шероховатости поверхности, варьируя преимущественно скоростью выглаживания.

При этом для многих эксплуатационных свойств деталей различной техники немаловажное значение имеет опорная способность шероховатости поверхности [56].

Опорная способность шероховатости поверхности после выглаживания возрастает, что иллюстрируется на рис. 1.6.  

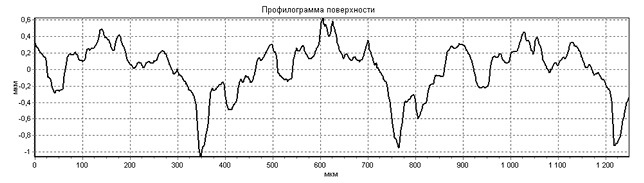
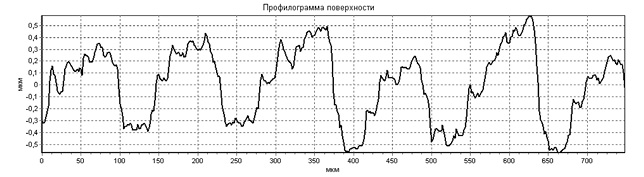
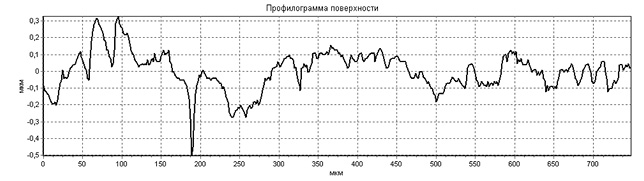
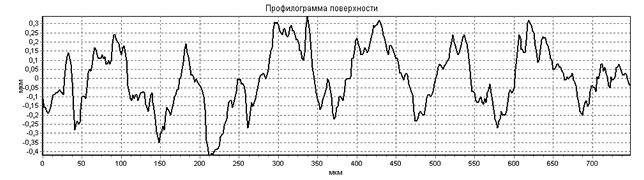
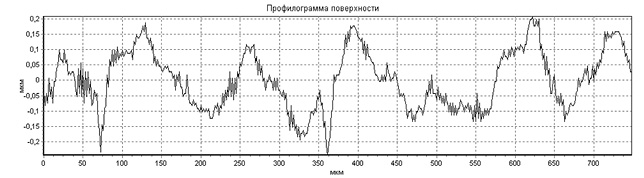
Рис. 1.5. Профилограммы выглаженных поверхностей

Таблица 1.1

Парная корреляция между Ra и другими параметрами шероховатости поверхности для различных условий выглаживания

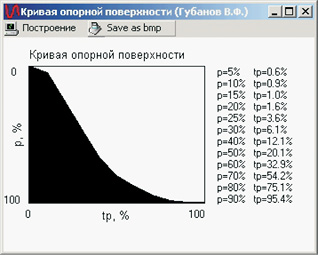
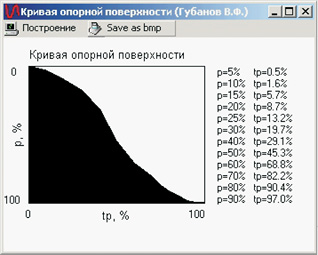
а                                           б  

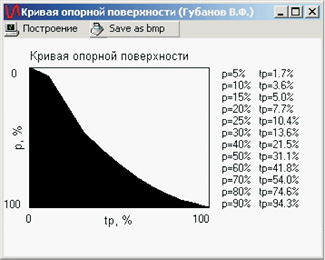
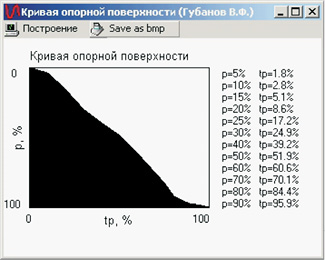
в                                         г

Рис. 1.6. Кривые опорной поверхности:
а, в, – обточенные поверхности;
б, г – соответствующие им выглаженные поверхности

Для оценки опорной способности шероховатости поверхности, можно использовать коэффициент χ_ш, характеризующий среднюю опорную способность шероховатости поверхности и рассчитывающийся через стандартизованные параметры шероховатости поверхности (Ra, мкм; Sm, мм; tср – относительная опорная длина профиля на уровне средней линии, %) по следующей формуле [17]:

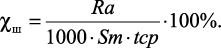(1.3)

Понятно, что чем меньше значение χш, тем выше опорная способность шероховатости поверхности, шероховатость получается «сглаженной». Если же, например, уменьшать значение Sm, шероховатость получится более «мелкоэлементной», и если деталь будет работать в условиях сухого трения с другой деталью, тогда эта «мелкоэлементность» приведет к более ускоренному изнашиванию деталей по сравнению со «сглаженной» шероховатостью.

Необходимо отметить, что подобный коэффициент можно использовать и по отношению к волнистости, заменив параметры шероховатости в формуле (1.3) на «аналогичные» параметры волнистости (Wa – среднее арифметическое отклонение профиля волн, мкм; Sm_w – средний шаг волн, мм; tср_w – относительная опорная длина профиля волн на уровне средней линии, %).

Коэффициент χв, характеризующий среднюю опорную способность волнистости поверхности:

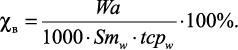(1.4)

На практике можно использовать коэффициент улучшения опорной способности шероховатости (υ_ш), который рассчитывается как отношение коэффициента χ_ши, характеризующего среднюю опорную способность исходной шероховатости поверхности (индекс «и» указывает, что используется параметр исходной шероховатости поверхности) к коэффициенту χ_ш, характеризующему среднюю опорную способность шероховатости поверхности после последующей операции (для волнистости аналогично):

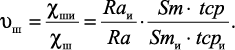(1.5)

Процесс выглаживания будет оправдан в качестве финишной операции по улучшению опорной способности исходной шероховатости поверхности, если после выглаживания υ_ш > 1,5.

По отношению к волнистости коэффициент улучшения опорной способности волнистости (υв):

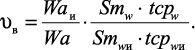(1.6)

Процесс выглаживания будет оправдан в качестве финишной операции по улучшению опорной способности исходной волнистости поверхности, если после выглаживания υ_в > 1,4.

Теоретические значения параметров шероховатости выглаженной поверхности, обусловленные кинематикой процесса и радиусом индентора (R), можно рассчитать по следующим формулам (при условии полного перекрытия исходной шероховатости и hз > Rmaxи):

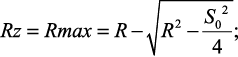[53] (1.7)

Ra ≅ 0,26Rz; (1.8)

Rp ≅ 0,666Rz; (1.9)

Sm = S₀; (1.10)

средний угол профиля шероховатости:

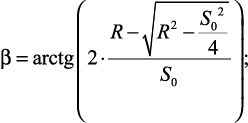(1.11)

отношение площади, не занятой материалом, к общей площади элементарной фигуры (прямоугольник), в которую вписана шероховатость (может выступать в качестве характеристики маслоемкости):

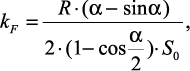(1.12)

где  

Анализ экспериментальных данных показывает, что, по сравнению с теоретическими значениями, реальные значения параметров шероховатости выглаженной поверхности могут существенно отличаться от теоретических значений. Это обуславливает необходимость обязательного учета как силы выглаживания (натяга) и скорости выглаживания, так и других факторов, что оправдывает наличие и использование для этих целей эмпирических формул.

Необходимо заметить, что любые эмпирические зависимости должны быть построены на базе теоретических зависимостей (например, исходя из кинематики, физики процесса) и должны уточнять их для конкретных условий обработки.

Например, для выглаживания, эмпирические зависимости должны иметь вид:

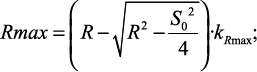            (1.13)

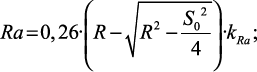           (1.14)

Sm = S₀·k_Sm,          (1.15)

где kRmax, kRa, kSm – коэффициенты, учитывающие влияние различных режимов и условий обработки на указанные параметры шероховатости, например: натяга, скорости выглаживания, автоколебаний.

Приведем простой пример, иллюстрирующий вышесказанное. При выглаживании стали 9ХС синтетическим алмазом с подачами 0,07…0,12 мм/об при радиусе индентора 3,5 мм и скорости выглаживания 30 м/мин при постоянном натяге обработка экспериментальных данных позволила получить следующую зависимость:

Rmax = (0,182·S₀)². (1.16)

В зависимости (1.16) «утрачены» данные о кинематике процесса, если же аппроксимировать данные, используя зависимость (1.13), тогда

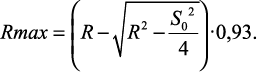(1.17)

Таким образом, какой-то фактор уменьшил реальные значения Rmax по сравнению с теоретическими значениями на 7 % (k_Rmax = 0,93). Оказалось, что это скорость выглаживания. Было установлено, что в диапазонах скоростей 20…70 м/мин (изменялся диаметр обработки):

k_Rmax = 0,78 + 0,005·V, (1.18)

следовательно,

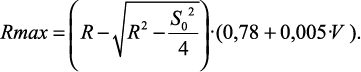(1.19)

Таким образом, в зависимости вида (1.19) мы учли и кинематику процесса (геометрический расчет), и скорость выглаживания, что невозможно, если использовать зависимость (1.16). Зависимости вида (1.19) можно развивать далее, учитывая натяг, автоколебания и технологическую наследственность [52, 57]. Например, наследование параметров шероховатости поверхности при выглаживании может быть представлено в виде схемы изображенной на рис. 1.7.  

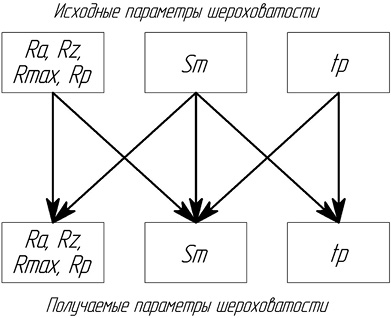
Рис. 1.7. Наследование параметров шероховатости
поверхности при выглаживании

Следует отметить, что при регулярном профиле исходной шероховатости поверхности получается регулярный профиль шероховатости выглаженной поверхности, в случае динамически устойчивой системы выглаживания.

Поскольку зависимости вида (1.19) «сложно» получать, если учитывается большое число факторов, влияющих на выходные значения процесса выглаживания, особенно при нелинейном влиянии режимов и других факторов на исследуемый параметр (что характерно для выглаживания), на практике широко применяются методы планирования эксперимента и обработки экспериментальных данных, которые, вероятно, еще долго будут использоваться при исследовании выглаживания, что обуславливается сложностью, многообразием и в определенном смысле «неоднозначностью» физических явлений и их последствий при выглаживании.

Следовательно, для реальных производственных условий, во многих случаях, быстрее и дешевле воспользоваться традиционными способами получения эмпирических формул, чем разрабатывать теоретические модели или хотя бы теоретико-экспериментальные. Поэтому, мы рассмотрим наиболее эффективное планирование эксперимента при выглаживании – некомпозиционное планирование [49] (обработка данных эксперимента второго порядка) на следующем примере.

Для установления многофакторной регрессионной модели процесса выглаживания синтетическим алмазом стали 9ХС, при радиусе индентора 3,5 мм, отражающей количественные связи между натягом, подачей, скоростью и параметром шероховатости – Ra был спланирован и поставлен эксперимент второго порядка.

Факторы и уровни варьирования факторов приведены в табл. 1.2.  

Таблица 1.2

Матрица плана эксперимента и результаты измерений Ra (мкм) представлены в табл. 1.3. В результате обработки экспериментальных данных, получена следующая зависимость:

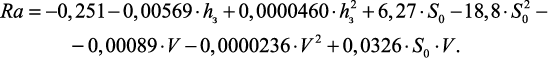(1.20)

Таблица 1.3

Матрица некомпозиционного плана второго порядка

Полученная зависимость [54] является наиболее характерной (типичной) для выглаживания. Необходимо заметить, что данные, полученные экспериментальным путем, достоверны лишь в пределах тех условий обработки, при которых они получены.