Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Выглаживание: качество, технологии и инструменты

Губанов В Ф,

1.5.2. Метод эталонов

Данный раздел основан на теоретических положениях, изложенных в работе [8], и в нем показывается, как применить эти положения к процессу выглаживания.

Пусть имеется эталонный признак вибросигнала (пэ1), характеризующий получение требуемого значения некоторого параметра качества поверхности и эталонный признак вибросигнала (пэ2), характеризующий неполучение требуемого значения параметра качества поверхности. В процессе обработки выглаживанием получаем значение признака вибросигнала (п). В качестве меры расстояния можно принять евклидово расстояние [8]:

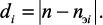(1.24)

Следовательно, если расстояние между полученным значением признака вибросигнала (п) и эталонным признаком вибросигнала (n_э1) меньше, чем между n и n_э2, (d₁ < d₂), то в этом случае предположительно обеспечивается требуемое значение параметра качества поверхности.

В случае, если имеется комплекс диагностических признаков, п = {п1, п2, .., пk}, соответственно и комплексы эталонных признаков, тогда взвешенное евклидово расстояние [8]:

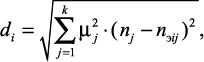(1.25)

где μ_j – вес, пропорциональный степени важности конкретного признака для диагностирования, 0 ≤ μj ≤ 1.

Например, при использовании в качестве признаков спектральных характеристик вибросигнала на нескольких частотах, весовыми коэффициентами могут быть относительные значения модуля передаточной функции на соответствующих частотах (т.к. амплитуды вибросигналов связаны с изменением силы выглаживания через передаточную функцию, зависящую от частоты [9, 33]), что позволяет учесть вклад частот в состояние диагностируемого объекта. C другой стороны, при изотопном (однородном) пространстве признаков, т.е. когда речь идет о параметрах одной физической природы (спектральные характеристики вибросигнала – амплитуды), все значения весовых коэффициентов можно принять равным единице (обычное евклидово расстояние), если все компоненты комплекса признаков одинаково важны для диагностирования.

Условие нормирования выглядит следующим образом [8]:

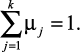(1.26)

На практике конкретные значения весовых коэффициентов можно назначить на основании экспертной оценки.

Допустим для диагностики микротвердости поверхности при выглаживании комплексы эталонных признаков состоят из трех признаков (амплитуд вибросигнала на трех частотах): n_э1 = {1, 4, 2}; n_э2 = {6, 20, 4}. Весовые коэффициенты, определенные поисковыми экспериментами, соответственно равны: μ = (0,3; 0,6; 0,1). В процессе диагностирования был получен следующий комплекс признаков: n = {3, 10, 4}. Следовательно

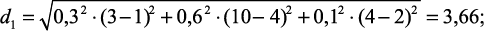
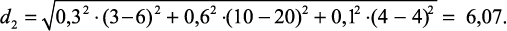
Т.к. d₁ < d₂, предположительно, обеспечивается требуемое значение микротвердости поверхности.

Очевидно, что надежность распознавания тем выше, чем меньше одно расстояние по сравнению с другим. Это можно охарактеризовать коэффициентом распознавания [8]:

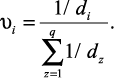(1.27)

Величина υi выполняет роль вероятности диагноза. Распознавание признается надежным, если υi больше заранее выбранного уровня распознавания υ0, т.е. при υ0 > υi. В нашем примере υ1 = 0,62; υ2 = 0,38, и если принять υ0 = 0,9, в этом случае без дополнительной информации нельзя однозначно утверждать, обеспечивается или нет требуемое значение микротвердости.

Следует заметить, что все признаки, входящие в комплекс диагностических признаков, n = {n1, n2, .., nk}, должны быть независимы друг от друга. В случае, если один признак зависит от другого, необходимо исключить один из зависящих признаков либо объединить их в комплексный признак (например, регрессионной моделью).

Таким образом, предварительная часть диагностики параметров качества по методу эталонов сводится к следующему:

• определить комплекс диагностических признаков;
• определить значения каждого признака пэ1 и пэ2;
• определить весовые коэффициенты;
• задать значение υ0.

В ходе выглаживания диагностика заключается в следующем:

• получить (измерить) комплекс диагностических признаков – п;
• рассчитать взвешенные евклидовы расстояния;
• выбрать di = min;
• рассчитать коэффициент распознавания для выбранного di и сравнить его с υ0;
• сделать вывод об обеспечении требуемого значения диагностируемого параметра качества.

На станках с программным управлением это даст возможность создать адаптивную систему управления формированием параметров качества поверхностного слоя деталей при выглаживании.