Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Бичурин М И, Петров В М,
3. МАКСВЕЛЛ-ВАГНЕРОВСКАЯ РЕЛАКСАЦИЯ МАГНИТОЭЛЕКТРИЧЕСКОГО ЭФФЕКТА
Хорошо известно, что увеличение свободных зарядов на границе разделов приводит к диэлектрической дисперсии и потерям в переменном электрическом поле, это явление известно как Максвелл-Вагнеровская релаксация. В данном разделе рассмотрена Максвелл-Вагнеровская релаксация МЭ параметров феррит-пьезоэлектрических композитов [32].
В качестве примера рассмотрим двухслойный композит со связностью типа 2-2, состоящий из магнитострикционной и пьезоэлектрической фаз. Формулы (1) и (2) используются для определения деформаций, электрической индукции и магнитной индукции для пьезоэлектрических и магнитострикционных фаз. С учетом конечной проводимости компонентов мы используем комплексные проницаемости
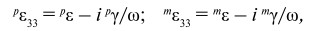
где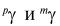 
являются проводимостями фаз; ω – круговая частота,
при этом w мала по сравнению с частотой электромеханического резонанса.
Слои должны быть тонкими и расположены в плоскости OX1X2. Пьезоэлектрическая компонента поляризована вдоль оси OX3, электрическое поле с круговой частотой w направлено вдоль той же оси, постоянное и переменное магнитные поля направлены вдоль оси OX1. В этом случае уравнения (4) для граничных условий приобретают вид:
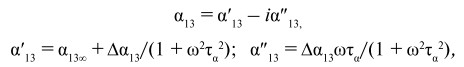(25)
Общий характер частотной зависимости магнитоэлектрической восприимчивости определяется формулами Дебая.
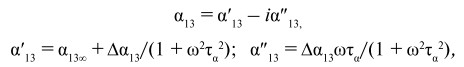(26)
где Δα13 = α130 – α13∞ – глубина релаксации, α130 и α13∞ являются статическими (при ωτα < < 1) и высокочастотными (при
ωτα >> 1) магнитоэлектрическими восприимчивостями, τα – время релаксации.
Статическая и высокочастотная МЭ восприимчивости, а также время релаксации может быть найдено путем решения уравнений (1) и (2) с учетом уравнения (25). Предполагая, что симметрия пьезоэлектрических фазы есть ∞m и симметрия магнитной фазы – кубическая, получим следующие выражения:
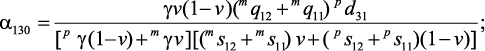(27)
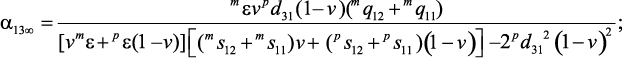
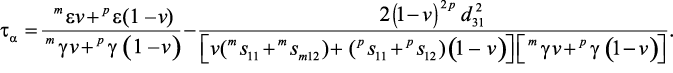
В качестве примера рассмотрим композит, состоящий из поляризованной сегнетоэлектрической керамики ЦТС и шпинели феррита никеля.
На рис. 12 показана гигантская релаксация МЭ восприимчивости. Большая глубина релаксации наблюдается в композите, состоящем из пьезоэлектрического компонента с большой проницаемостью феррита и с большой проводимостью. В случае, если mε/pε << 1 и pγ/mγ << 1 максимум глубины релаксации наблюдается при объемной доли пьезоэлектрической фазы v1 ≈ [(ps11 + ps12)/(ms11 + ms12)]1/2 (pγ/mγ)1/2. Принимая податливости обоих компонентов равными, можно получить v1 ≈ (pγ/mγ)1/2. При pγ/mγ << v << 1 статическая МЭ восприимчивость приближается к пиковому значению (mq12 + mq11) pd31/(ps11 + ps12). Для рассматриваемого случая v1 = (ph/mh)1/2 ≈ 10–4 (где ph и mh – толщины пьезоэлектрической и ферритовой компонент), а максимальное значение МЭ восприимчивости составляет 0,94•10–8 с/м. Большая магнитоэлектрическая восприимчивость обусловлена сильным электрическим полем в пьезоэлектрической компоненте при малой толщине и значительной проводимости ферритового слоя, а также большими внутренними механическими напряжениями pTj и mTj (j = 1,2). Эти напряжения вызваны электрическим полем в пьезоэлектрической компоненте. Максимальное значение МЭ восприимчивости композитов превышает 10–8 s/м. (для сравнения, МЭ восприимчивости Cr2O3 составляет 1,1•10–11 s/m).
В случае слабого пьезоэлектрического эффекта (d312/[(ps11 + ps12) pε] << 1) время релаксации, как следует из уравнения (27), при pγ/mγ << v/(1 – v) в основном определяется временем зарядки пьезоэлектрического слоя через сопротивление ферритового слоя: τα ≈ (pε/mγ)(1 – v)/v. Увеличение объемной доли пьезоэлектрической фазы приводит к быстрому уменьшению времени релаксации. Усиление пьезоэлектрического эффекта приводит к увеличению второго члена в формуле (27), описывающего пьезоэлектрические свойства композитов. Механические напряжения pT1 и pT2, возникающие благодаря поперечному пьезоэлектрическому эффекту, приводят к дополнительному заряду на пьезоэлектрическом слое и в результате ведут к снижению времени зарядки и времени релаксации МЭ восприимчивости. Время релаксации и частота релаксации ωr = 1/τα соответствуют пику мнимой части МЭ восприимчивости, которая может варьироваться в широких пределах путем изменения объемных долей компонентов, а также выбором параметров компонентов (рис. 13). Зависимость времени релаксации от объемной доли ЦТС показана на рис. 14.
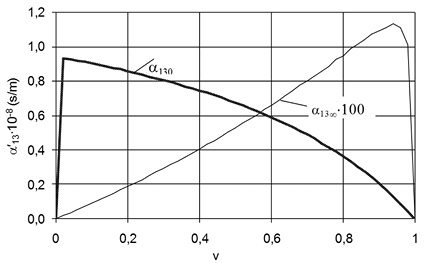
Рис. 12. Зависимость статической и высокочастотной МЭ
восприимчивостей от объемной доли ЦТС
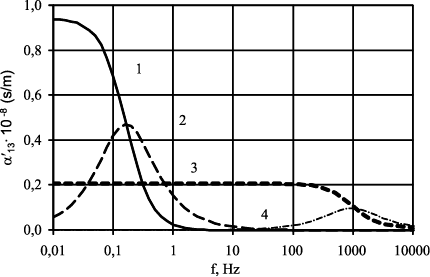
Рис. 13. Частотная зависимость действительной (1, 3) и мнимой (2, 4) частей МЭ восприимчивости: 1, 2 – v = 0,001, 3, 4 – v = 0,9
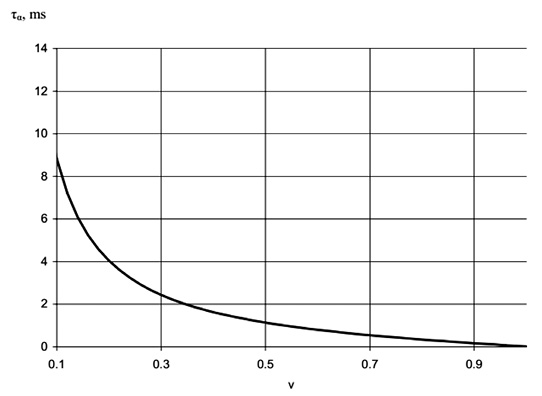
Рис. 14. Зависимость времени релаксации
от объемной доли ЦТС для МЭ восприимчивости
Частотная зависимость магнитоэлектрического коэффициента αE,T = E3/H1 определяется формулами Дебая аналогичным уравнениям (26):
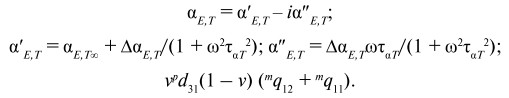(28)
В отличие от магнитоэлектрической восприимчивости, действительная часть магнитоэлектрического коэффициента увеличивается с частотой, т.е. его релаксация имеет обратный характер (рис. 15).
Пик глубины релаксации достигается при v ≈ 0,5. В случае слабого пьезоэлектрического эффекта (d312/[(ps11 + ps12) pε] << 1) время релаксации определяется в основном временем разрядки пьезоэлектрического слоя через собственное сопротивление ταT ≈ pε/pγ и не зависит от объемной доли компонентов, при этом ταT >> τα. При усилении пьезоэлектрического эффекта, как следует из уравнения (28), уменьшается время релаксации. Этому способствует снижение заряда на пьезоэлектрическом слое пластины конденсатора под влиянием механических напряжений pT1 и pT2 в результате приложения внешнего магнитного поля. Рис. 16 показывает МЭ коэффициент по напряжению при изменении объемной доли ЦТС.
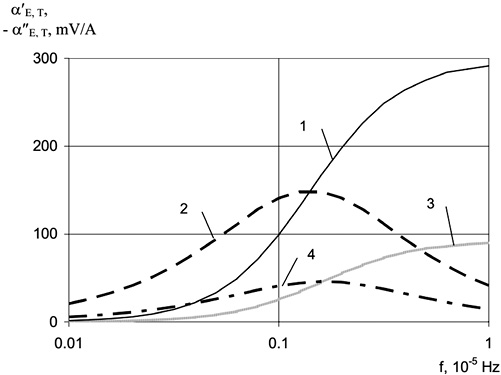
Рис. 15. Частотная зависимость действительной (1, 3) и мнимой (2, 4) частей МЭ коэффициента по напряжению: 1, 2 – v = 0,1; 3, 4 – v = 0,5
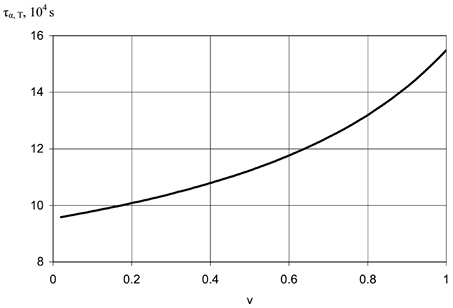
Рис. 16. Зависимость времени релаксации МЭ коэффициента по напряжению от объемной доли ЦТС
Следует отметить, что изменение связности композита приводит к изменению кривой релаксации. В случае объемного композита со связностью типа 3-0 частотная зависимость МЭ коэффициента состоит из двух областей релаксации [33].