Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретическое моделирование магнитоэлектрического эффекта в магнитострикционно-пьезоэлектрических наноструктурах

Бичурин М И, Петров В М,

1.3. Изгибные колебания двухслойной структуры на подложке

Теоретическое моделирование низкочастотного МЭ эффекта, описанное выше, основано на рассмотрении однородных продольных деформаций. Однако, конфигурационная асимметрия двухслойной структуры подразумевает изгиб образца при приложении магнитного или электрического поля и изменение индуцируемого поля. Одной из принципиальных задач настоящей работы является моделирование МЭ взаимодействий в магнитострикционно-пьезоэлектрической двухслойной наноструктуре на подложке с учетом изгибных деформаций [23, 27, 59]. Для численных оценок выбрана модель ФН-ЦТС на подложке из SrTiO3. Исследованы двухслойные эпитаксиальные наноструктуры из ФН и ЦТС, выращенные на подложке из SrTiO3 [21]. Мы рассчитали МЭ коэффициент по напряжению αE для поперечной ориентации полей, чтобы обеспечить минимальные размагничивающие поля и максимальное значение αE.

В расчетах полагается, что симметрия пьезоэлектрика – ∞m, а пьезомагнетика – кубическая. Как показано на рис. 5, xm, xp и xs – нейтральные оси, расположенные в горизонтальной срединной плоскости пьезомагнитного, пьезоэлектрического слоев и слоя подложки соответственно, которые разделены расстояниями hm и hp. Толщина пластины принимается малой по сравнению с остальными размерами.  

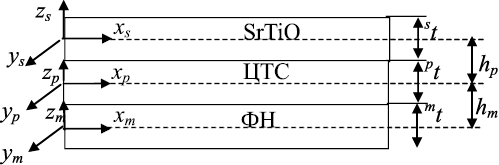
Рис. 5. Схема двухслойной структуры на подложке

Для учета изгиба образца будем считать, что продольные осевые силы каждого слоя являются линейными функциями от вертикальной координаты zi. В соответствии с условием равновесия структуры сумма осевых сил в трех слоях равна нулю.

F_p1 + F_m1 + F_s1 = 0, (12)

где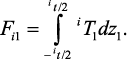

Суммарный вращающий момент также равен нулю для образца, находящегося в равновесии:

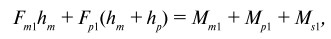(13)

где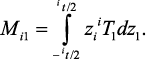  

Совместное решение уравнений (12) и (13) с учетом выражений (10) позволяет найти аксиальные напряжения в пьезоэлектрическом слое pT1 и pT2. Тогда выражение для МЭ коэффициента по напряжению, используя условие разомкнутой цепи, может быть выражено

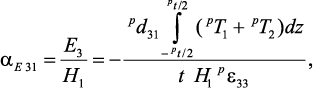(14)

где t = mt + pt + st – общая толщина исследуемой структуры.

В случае отсутствия изгибных деформаций можно легко показать, что выражение для МЭ коэффициента по напряжению приводится
к известному выражению, которое получается при предположении об однородных продольных деформациях.