
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.1. Магнитоэлектрический эффект в области продольной моды
В дальнейшем мы рассмотрим колебания низкой частоты, т. е. объемные колебания, распространяющиеся вдоль границы.
Решение уравнения движения среды должно быть получено с учетом уравнений магнитостатики и эластостатики, материальных уравнений, закона Гука, эффекта несоответствия кристаллических решеток и граничных условий. Уравнение движения среды имеет вид:
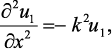 (19)
(19)
где u1 – смещение в направлении оси x. Волновое число k определяется выражением:
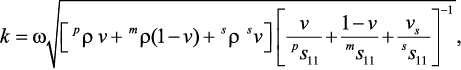 (20)
(20)
где ω – круговая частота, pρ, mρ и sρ – плотности пьезоэлектрической, пьезомагнитной фаз и подложки, где v = pv/(pv + mv), vs = sv/(pv + mv). Через pv, mv и sv обозначены объемы пьезоэлектрической и магнитострикционной фаз и подложки.
Для решения уравнения (19), используются следующие граничные условия:
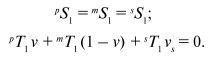 (20)
(20)
МЭ коэффициент по напряжению αE 13 = E3/H1 рассчитывается численно по формулам (9), (19) и (21), при этом используется условие разомкнутой цепи D3 = 0. Чтобы принять во внимание потери энергии, используется комплексная частота ω = ω′ –iω″ при ω″/ω′ = 10–3.
Резонансное усиление ME коэффициента по напряжению для свободной двухслойной структуры наблюдается на антирезонансных частотах (рис. 8).
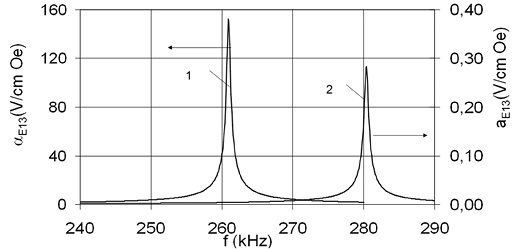
Рис. 8. Частотная зависимость МЭ коэффициента по напряжению
αE,13 = δE3/δH1
для свободной двухслойной структуры (1) и для двухслойной структуры на
подложке SrTiO3 при vs = 5 (2). Расчет выполнен для v = 0,5
Для свободной наноструктуры увеличение αE 13 наблюдается при увеличении объема титаната бария и достигает максимального значения 280 В/смЭ при v = 0,5, а затем падает с ростом v. Резкое уменьшение αE 13 показано на рис. 8, когда структура CFO-BaTiO3 нанесена на подложку SrTiO3. Это уменьшение обусловлено (i) эффектом зажатия подложки и (ii) изменением пьезоэлектрических и пьезомагнитных коэффициентов, диэлектрической проницаемости вследствие эффекта несоответствия кристаллических решеток. На рис. 9 показано изменение максимального значения αE 13 как функции объемной доли подложки vs, а также изменение частоты ЭМР, соответствующей пику αE 13. Как видно на рис. 9, дальнейшее увеличение vs приводит к существенному уменьшению αE 13 и МЭ коэффициент обращается в ноль для объемной доли SrTiO3 20 и больше. Сдвиг частоты ЭМР в сторону больших значениий, соответствующих максимальному МЭ эффекту, обусловлен изменением эффективной податливости образца при увеличении толщины подложки.
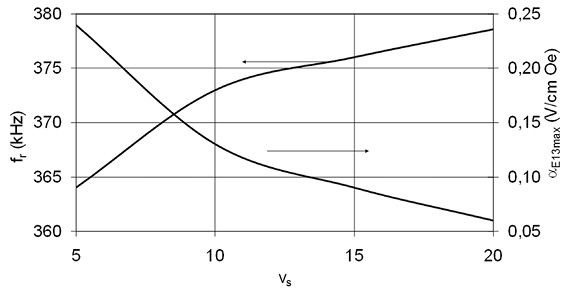
Рис. 9. Зависимость максимального значения МЭ коэффициента по напряжению αE,13 и соответствующей частоты ЭМР fr от объемной доли подложки vs
Таким образом, предложена модель ME взаимодействия в феррит-пьезоэлектрических слоистых наноструктурах на подложке. Для двухслойной структуры CFO-BaTiO3 на подложке с увеличением толщины подложки (i) МЭ коэффициент экспоненциально уменьшается, а (ii) частота ЭМР увеличивается.
