
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2. Магнитоэлектрический эффект в области изгибной моды
Основным недостатком резонансного MЭ эффекта на продольных модах ЭМР является то, что резонансные частоты очень высокие, порядка сотен кГц, для номинальных размеров образца. На таких частотах, потери на вихревые токи в магнитострикционной фазе могут быть существенными, в частности, для редкоземельных сплавов, таких как Терфенол-Д, в результате МЭ преобразования энергии становится неэффективным. В целях снижения рабочей частоты, можно использовать ME эффект в области изгибной моды ЭМР [23, 27].
В этом разделе представлена теоретическая модель изгибных
колебаний двухслойной пластины, которая формируется из
магнитострикционных и пьезоэлектрических нанослоев, выращенных на
подложке.
Подмагничивающее поле предполагается приложенным
к магнитострикционным компонентам в плоскости образца, чтобы
уменьшить размагничивающие поля. Предполагается, что толщина пластины
мала по сравнению с остальными размерами. Кроме того, предполагается,
что ширина пластина мала по сравнению с его длиной. В этом случае мы
можем рассматривать только один компонент тензоров деформаций
и напряжений в области ЭМР. Уравнения изгибных колебаний двухслойной
пластины имеет вид:
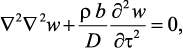 (22)
(22)
где ∇2∇2 – бигармонический оператор; w – прогиб (смещение
в направлении z); t и ρ являются толщиной и средней плотностью образца,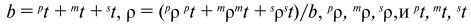 –
плотности и толщины пьезоэлектрических и пьезомагнитных слоев
и подложки соответственно, и D – цилиндрическая жесткость образца.
–
плотности и толщины пьезоэлектрических и пьезомагнитных слоев
и подложки соответственно, и D – цилиндрическая жесткость образца.
Граничные условия при x = 0 и x = L должны быть использованы для нахождения решения этого уравнения. Здесь L является длиной двухслойной структуры. В качестве примера, рассмотрим пластину со свободными краями. На свободном конце, крутящий момент M1 и поперечная сила V1 равны нулю:
M1 = 0 и V1 = 0 при x = 0 и x = L, (23)
где 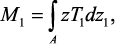
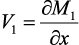 и A является площадью поперечного сечения образца перпендикулярно оси х.
и A является площадью поперечного сечения образца перпендикулярно оси х.
Мы заинтересованы в динамическом МЭ эффекте, когда к образцу прикладывается переменное магнитное поле H, а измеряется среднее индуцированное электрическое поле Е. МЭ коэффициент по напряжению вычисляется по формуле αE = E/H. При использовании условия разомкнутой цепи МЭ коэффициент по напряжению может быть найден как
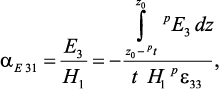 (24)
(24)
где E3 и H1 среднее индуцируемое электрическое поле и приложенное магнитное поле. Для учета потерь энергии используем комплексную частоту ω = ω′ + iω′′ при ω′′/ω′ = 10–3.
В качестве примера оценим МЭ коэффициент, используя уравнение (24), для двухслойной структуры на основе пермендюра и ЦТС.
На
рис. 10 показана частотная зависимость МЭ коэффициента по напряжению на
изгибной моде для двухслойной пластины с длиной 9,15 мм и толщиной
3,22 мм для объемной доли ЦТС, равной 0,67. График показывает гигантское
значение αE,31 = 6,6 В/смЭ.
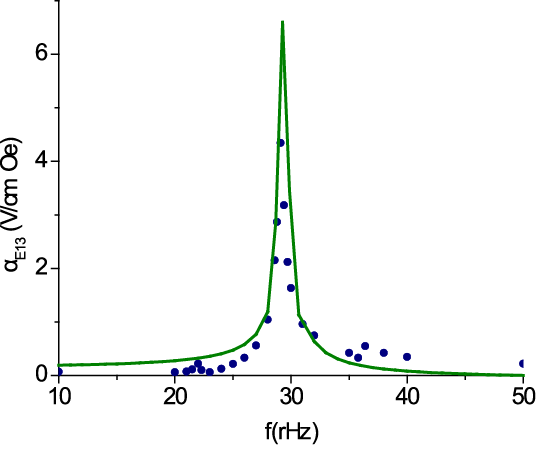
Рис. 10. Теоретическая (сплошная линия) и измеренная (кружки) частотная зависимость поперечного ME коэффициента по напряжению для двухслойной структуры пермендюр-ЦТС со свободными концами для V = 0,67
Размещение двухслойной структуры ФН – ЦТС на подложке из SrTiO3 приводит к изменению ME коэффициента, как показано на рис. 11. При малых значениях толщины подложки ME коэффициент значительно уменьшается и обращается в нуль при отношении толщин подложки и двухслойной структуры Vs = 0,3. Это объясняется уменьшением среднего механического напряжения в пьезоэлектрической компоненте. Дело в том, что часть этого слоя подвергается растяжению, в то время как вторая часть – сжатию. Согласно формуле (52), индуцированное электрическое поле определяется средним значением механического напряжения.
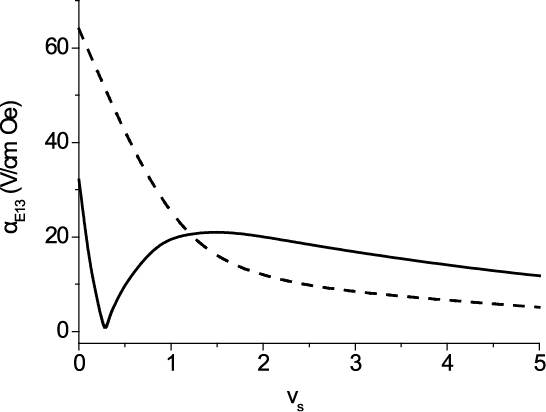
Рис. 11. Зависимость максимального значения МЭ коэффициента по напряжению для двухслойной структуры ФН – ЦТС в области изгибной моды от отношения толщины подложки SrTiO3 к толщине двухслойной структуры для объемной доли ЦТС 0.6. Для сравнения пунктирной линией показан МЭ коэффициент по напряжению для продольной моды
Следует отметить, что максимальный МЭ коэффициент по напряжению изгибной моды больше, чем в области продольной моды, более чем в два раза при Vs > 2, как показано на рис. 11. Частота ЭМР почти линейно зависит от толщины подложки.
