Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Бичурин М И, Петров В М,
1.1.1. Продольный магнитоэлектрический эффект
Обозначим через (1,2) поверхность пленки, а через 3 – направление перпендикуляра к плоскости образца.
Двухслойная структура поляризована электрическим полем с напряженностью Е вдоль направления 3. Подмагничивающее поле Н и переменное магнитное поле δH направлены в том же направлении, что и поле Е, а результирующее индуцированное электрическое поле δE измеряется на электродах образца. МЭ коэффициент по напряжению определяется как α′E,L = α′E,33 = δE3/δH3. Для этого случая ненулевые коэффициенты psij pdki, msij, mqki, sij, dki, qki, αkn приведены в [23]. Уравнения (1)–(3) решаются относительно следующих граничных условий:
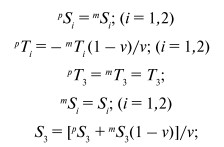(4)
где v = pv/(pv + mv), а pv и mv – объемные доли пьезоэлектрической и магнитострикционной фаз соответственно.
Для определения эффективных пьезоэлектрического
и магнитострикционного коэффициентов необходимо рассматривать композит
в электрическом поле E3 = V/t (где V – приложенное напряжение, а t –
толщина композита) и магнитном поле H3. Эффективное поле Е
в пьезоэлектрической и эффективное поле Н в магнитострикционной фазе
можно получить как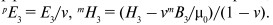 
. Используя
непрерывность компонент магнитного и электрического полей и индукций,
а также условия разомкнутой и замкнутой цепи, можно получить следующие
выражения для продольного МЭ коэффициента по напряжению.
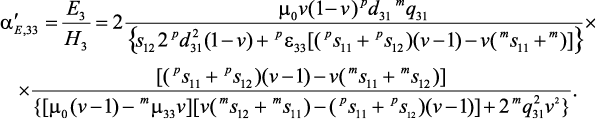(5)
Харше и др. получили выражение для продольного МЭ коэффициента в другой форме [24]:
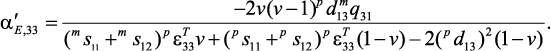(6)
Выражение (6) соответствует частному случаю нашей теории, при котором принимается mμ33/μ0 = 1. Таким образом, рассмотренная здесь модель приводит к выражению для продольного МЭ коэффициента и позволяет оценить его как функцию от объемной доли фаз (рис. 1).
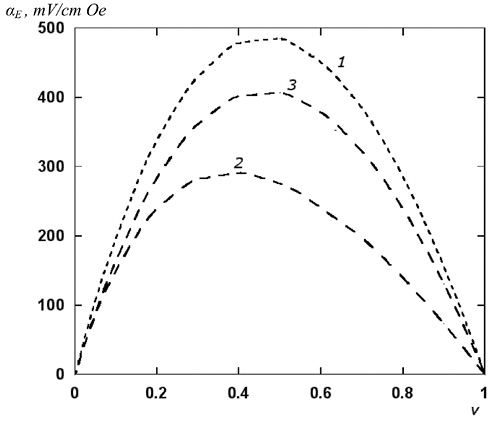
Рис. 1. Концентрационная зависимость МЭ коэффициента по напряжению
для свободного образца композита состава феррит кобальта – титанат
бария:
1 – поперечная ориентация полей; 2 – продольная ориентация;
3 –коэффициент pE3/mH3