Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Бичурин М И, Петров В М,
4.5.1. Нормально намагниченный образец
Выражения (74)-(76) для гармонической волны, распространяющейся вдоль оси z, могут быть приведены к следующей форме:
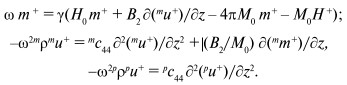(78)
где ω – угловая частота, а mρ и pρ – плотности ферритового и пьезоэлектрического слоев.
Уравнение движения для ферритового слоя может быть приведено к виду, предполагая, что H однородно по объему образца:
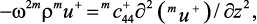(79)
где эффективный модуль упругости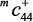 
определяется как
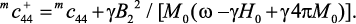(80)
В уравнении (80) учитывается пространственная переменная намагниченность. Граничные условия на верхней (ферритовой) и нижней (ЦТС) сторонах могут быть записаны в виде:
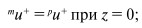
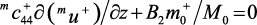при z = mL;
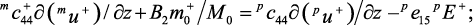при z = 0; (81)
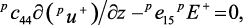при z = – pL,
где mL и pL – толщины ферритового и пьезоэлектрического слоев, m0+ = –γM0/(ω – γH0 + γ4πM0) – переменная намагниченность, однородная по объему образца. Как видно из формулы (81), механическое смещение и однородная прецессия намагниченности для феррита связаны через граничные условия на границе. Напряженность E+ индуцированного электрического поля в ЦТС может быть найдена с помощью условия разомкнутой цепи:
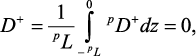(82)
где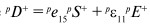 
– электрическое смещение, а pe11 –
диэлектрическая проницаемость пьезоэлектрической фазы при постоянной
деформации. Подставляя корень уравнения (78) в уравнение (82) и принимая
во внимание выражения (74) и (81), можно получить выражение для
магнитоэлектрического коэффициента по напряжению [54]:
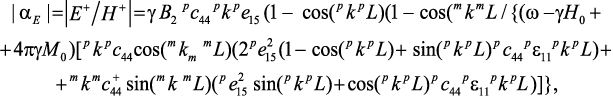(83)
где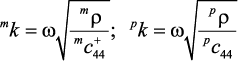 
.
Теперь мы применим теорию к конкретной двухслойной системе ЖИГ-ЦТС. Необходимым условием для наблюдения сильного MЭ эффекта в области МАР является наличие малых потерь в ЖИГ при ФМР. Предполагаемые толщины для ЖИГ и ЦТС таковы, что толщинный резонанс имеет место в диапазоне 5-10 ГГц, т.е в диапазоне частот ФМР в насыщенном состоянии ЖИГ. Мы рассматриваем MЭ эффект при подмагничивающих полях, соответствующих магнитному резонансу. Резонансное поле Hr определяется условием:
Hr = ω /γ - 4πM0.
При увеличении H0 до величины Hr МЭ коэффициент увеличивается и имеет резонансную форму благодаря резонансной частотной зависимости механического смещения в области ФМР. Рис. 27 и 28 показывают оценки αE в зависимости от f. Ослабление сигнала учитывается в этих расчетах путем введения комплексной частоты, у которой мнимая часть ω′′ = 107 рад/с.
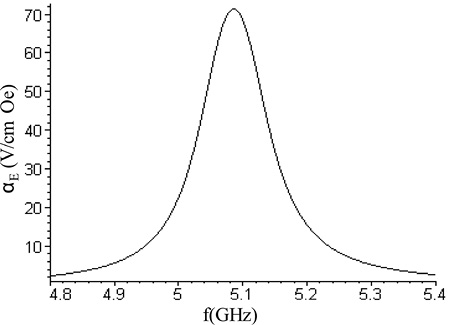
Рис. 27. Частотная зависимость МЭ коэффициента по напряжению для двухслойной структуры состава ЦТС (100 nm) – ЖИГ (195 nm) для подмагничивающего поля 3570 Oe
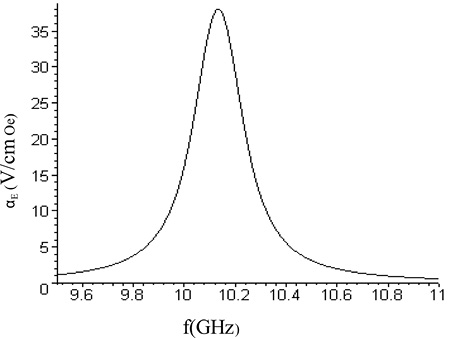
Рис. 28. Частотная зависимость МЭ коэффициента по напряжению для двухслойной структуры состава ЦТС (100 nm) – ЖИГ (195 nm)
для подмагничивающего поля 5360 Oe. Частота ФМР совпадает
с частотой второй гармоники ЭМР