Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретическое моделирование магнитоэлектрического эффекта в магнитострикционно-пьезоэлектрических наноструктурах

Бичурин М И, Петров В М,

4.5.2. Касательно намагниченный образец

Для касательного подмагничивания можно получить следующее выражение для МЭ коэффициента по напряжению [55]:

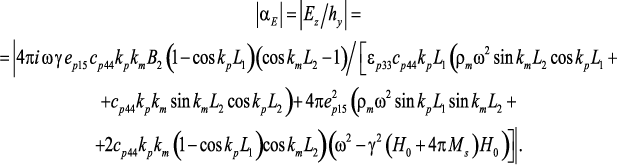(84)

На рис. 29 показана частотная зависимость при двух значениях поля смещения H0 – 1130 Э и 2840 Э для структуры ЖИГ-ЦТС с толщинами пьезоэлектрического и ферритового слоев 100 и 195 нм, соответственно. Потери энергии были учтены использованием комплексной частоты ω = ω’ + iω’’, где ω’’ – параметр, описывающий потери. Резкий пик на частотной зависимости MЭ коэффициента по напряжению наблюдается для подмагничивающего поля, которое соответствует совпадению частоты ФМР и частоты первого толщинно-сдвигового резонанса двухслойной структуры (рис. 29а). Как только подмагничивающее поле H0 увеличивается до 2840 Э, частота ФМР совпадает со второй частотой ЭМР двухслойного образца (рис. 29b).  

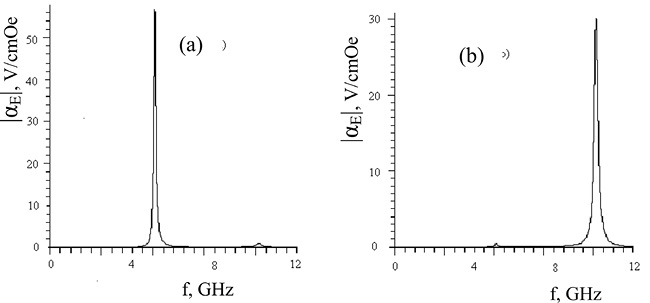
Рис. 29. Частотная зависимость МЭ коэффициента по напряжению для двухслойной структуры состава ЦТС (100 nm) – ЖИГ (195 nm) для тангенциального подмагничивающего поля 1135 Oe (а) и 2835 Oe (б)

В отличие от магнитоакустического резонанса в нормально намагниченной пленке, резонанс в тангенциально намагниченной двухслойной структуре происходит при меньшем подмагничивающем поле.

Толщина ферритового слоя (195 нм) соответствует максимальному МЭ эффекту в тангенциально намагниченном образце, но он меньше, чем при нормальном намагничивании. Это обстоятельство связано с зависимостью эффективной жесткости феррита от величины и направления подмагничивающего поля. Действительно, выражение (78) приводит к следующему дисперсионному отношению:

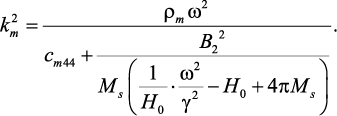(85)

Выражение (85) показывает, что изменяющаяся в пространстве часть намагниченности (связанная с упругим смещением) вносит вклад в эффективный модуль упругости (второй член в знаменателе) посредством магнитоупругой связи.

Результаты расчетов MЭ коэффициента по напряжению показывают, что композиты, состоящие из монокристаллических ферритов и пьезоэлектриков, являются перспективными материалами для создания устройств, использующих генерацию магнитоупругих волн или электрически управляемый магнитный резонанс.