Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Лекция 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ – СЖАТИЕ
Внутренние силы в поперечных сечениях стержня. Построение эпюр внутренних сил от действия внешних сил. Напряжения в поперечных сечениях стержня. Деформации продольные и поперечные, коэффициент Пуассона. Закон Гука. Модуль упругости. Определение перемещений поперечных сечений стержня. Построение эпюр напряжений и перемещений.
Растяжение – сжатие. Растяжение и сжатие – это наиболее простые и часто встречающиеся виды деформации. На растяжение и сжатие работают многие элементы конструкций: стержни ферм, колонны, канаты лебедок, штоки паровых машин, лонжероны крыла самолетов. Растяжение и сжатие – это наиболее простые виды деформации, поэтому изучение курса сопромата начинается именно с изучения этих видов деформации.
Внутренняя продольная сила (или нормальная сила). При растяжении или сжатии в поперечных сечениях бруса возникает только один внутренний силовой фактор – внутренняя продольная сила N (рис. 5). Брус имеет два характерных участка. Для определения продольной силы N воспользуемся методом сечения. На расстоянии y1 проведем сечение на первом участке и рассмотрим равновесие отсеченной части. Продольную силу будем всегда показывать от сечения, что будет соответствовать растяжению бруса.
Составим условие равновесия на ось y
N1 – F = 0,
откуда
N1 = F.
Проведем на втором участке сечение на расстоянии y2. Рассматривая равновесие отсеченной части, получаем N2 = F. Строим эпюру продольных сил.
Нормальные напряжения. Исходя из определения напряжения, можно записать
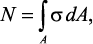 (1)
(1)
где σ – нормальное напряжение в произвольной точке сечения.
Согласно гипотезе плоских сечений (гипотезаБернулли) все продольные волокна бруса деформируются одинаково, а это означает, что напряжения в поперечных сечениях одинаковы, т.е. σ = const.
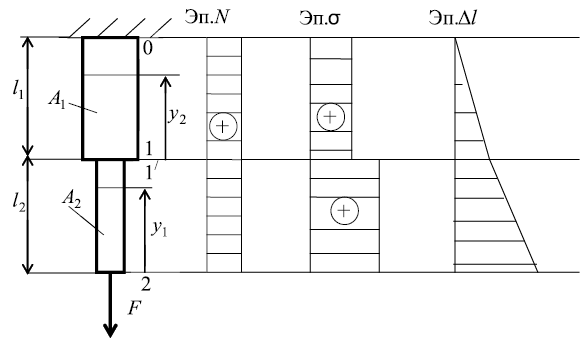
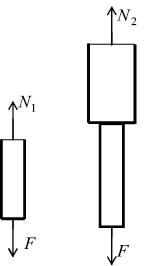
Рис. 5. Построение эпюр N, σт, Δl
В этом случае получаем
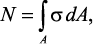
откуда .
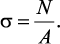
Рассчитывая напряжения в каждом сечении, строим эпюру нормальных напряжений (рис. 5).
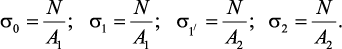
Деформации и перемещения.
Величина, на которую изменится длина бруса (или одного из его участков) под действием продольных сил, называется продольной деформацией (рис. 6). Относительная продольная деформация – отношение абсолютной продольной деформации Dl к первоначальной длине стержня l:
ε = Dl/l0
Величина Δа (Δb), на которую изменится размерпоперечного сечениябруса а (b) под действием продольной силы, называется поперечной деформацией.
Отношение абсолютной поперечной деформации, Dа (Db) к первоначальному размеру сечения бруса а (b), называется относительной поперечной деформацией:
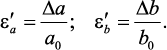
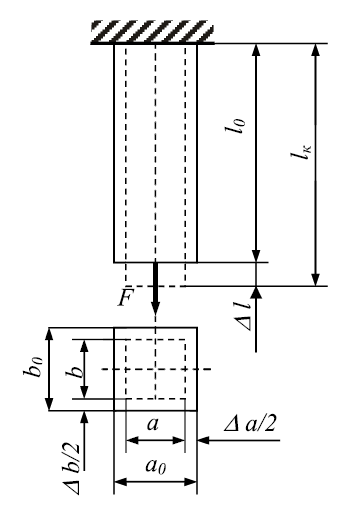
Рис. 6. Схема деформирования стержня