Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Лекция 7. КРУЧЕНИЕ
Крутящие моменты (внутренний силовой фактор) в поперечных сечениях стержня. Кручение стержней круглого поперечного сечения: допущения, деформации, напряжения, углы закручивания. Условия прочности, жёсткости. Построение эпюр крутящих моментов.
Кручение имеет место в случае действия на вал момента (пары сил) относительно его продольной оси, и в поперечных сечениях бруса возникает только один силовой фактор – крутящий момент. Брус, работающей на кручение называется валом. При кручении вала его поперечные сечения поворачиваются друг относительно друга, вращаясь вокруг оси бруса.
Напряжения и деформации при кручении бруса. Под действием внешнего
скручивающего момента, приложенного на правом конце бруса, левый конец
которого жестко закреплен, брус будет закручиваться. Выделим из бруса
элементарный цилиндр длиной dx (рис. 19). Будем считать, что левое
сечение бруса жестко закреплено. Под действием крутящего момента T
правое сечение повернется на некоторый угол dφ.Так как ds = γ•dx = ρ•dφ,
то получаем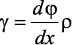 
. Из данной зависимости видно, что угол сдвига γ изменяется по радиусу вала по линейному закону.
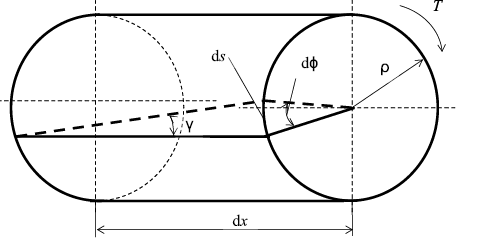
Рис. 19. Расчетная схема при кручении
Деформация бруса при кручении характеризуется относительным углом закручивания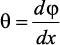 
.
При малых углах закручивания вала в теории кручения круглых стержней принимаются допущения:
1. Поперечные сечения, плоские и перпендикулярные к его оси до деформации, остаются плоскими (не коробятся) и перпендикулярными к оси вала и после деформации (гипотеза Бернулли).
2. Радиусы поперечных сечений при деформации не искривляются и не изменяют своей длины.
3. Длина вала в результате закручивания не изменяется.
Поперечное сечение вала ведет себя при кручении, как жесткий диск, и деформацию кручения можно рассматривать, как результатсдвига одного поперечного сечения относительно другого. В этом случае в точках поперечного сечения вала возникают только касательные напряжения.
Теория кручения, основанная на упомянутых допущениях, подтверждается экспериментальными данными.
Согласно закону Гука при сдвиге, имеем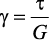 
. Откуда получаем:
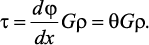
Из полученной зависимости следует, что касательные напряжения изменяются по радиусу по линейному закону.
При кручении все внутренние силы, распределенные по поперечному сечению, приводятся к одной составляющей – к крутящему моменту. Касательные напряжения перпендикулярны радиусам, проведенные через точки их действия (рис. 20). Крутящий момент T в сечении бруса определяется по формуле
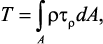
где ρ – плечо элементарной силы.
Подставляя значение касательного ускорения, получим
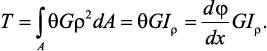(8)
Элементарный угол закручивания бруса: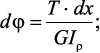 
полный угол закручивания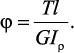 
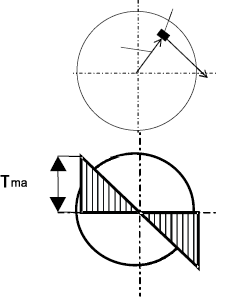
Рис. 20. Эпюра
Максимальное касательное напряжение в поперечном сечении бруса будет определяться по зависимости:
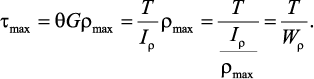
Прочность и жесткость при кручении. Условие прочности при кручении имеет вид
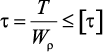
Условие жесткости:
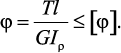(9)
Для бруса круглого сечения эти условия принимают вид:
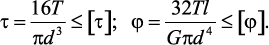
Построение эпюр крутящих моментов. Крутящий момент, возникающий в поперечном сечении стержня, определяется методом сечений. Крутящий момент равен алгебраической сумме скручивающих моментов, приложенных к любой из частей стержня. Эпюра крутящих моментов – это график, показывающий изменения крутящего момента по длине вала. Правило знаков для эпюры крутящих моментов
При построении эпюры крутящих моментов используется правило знаков: скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки при взгляде на поперечное сечение, вызывает в этом сечении положительный крутящий момент.
Брус разбивается на участке, на каждом участке проводится сечение и определяется крутящий момент. Затем строится эпюра крутящих моментов.
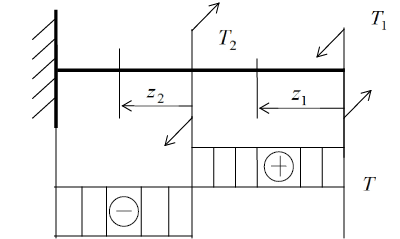
Рис. 21. Эпюра крутящих моментов