Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Лекция 10. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ ПО МЕТОДУ СИЛ
Степень статической неопределимости. Решение канонических уравнений метода сил.
Расчет статически неопределимой системы начинается с нахождения степени ее статической неопределимости, которая может быть установлена по формуле:
Л = 3К – Ш.
В методе сил за основные («лишние») неизвестные силы принимаются реактивные силы в отброшенных связях системы. Вычислив количество лишних связей, приступают к выбору основной системы и назначению неизвестных. Основной явится та статически определимая система, которая получена из заданной статически неопределимой после устранения лишних связей. Желательно получить наиболее простую основную систему.
После этого составляются канонические уравнения. В общем случае они запишутся в следующем виде:
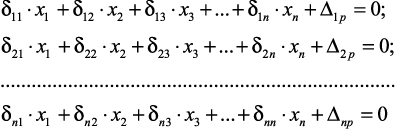(22)
Физический смысл уравнений: перемещение по направлению каждой неизвестной сил от всех неизвестных сил и от заданной нагрузки должно равняться нулю, так как в заданной системе имеются связи по направлению неизвестных сил.
Каждый коэффициент при неизвестном, входящем в каноническое
уравнение (δ11, δ12, δnn),есть перемещение основной системы по
направлению неизвестных от единичных сил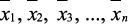 
.
Свободные члены уравнения (δ1p, δ2p, δnp) представляют собой
перемещения основной системы по направлению неизвестных от заданной
нагрузки.
Коэффициенты при неизвестных и свободные члены канонических уравнений определяются с помощью интеграла Мора по формулам
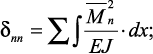
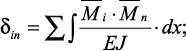(23)
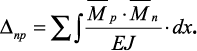
Если в раме стержни прямолинейны и по длине имеют одинаковую жесткость, то можно определить коэффициенты при неизвестных и свободные члены по правилу А.Н. Верещагина (перемножением эпюр) по выражениям
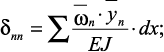
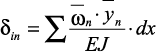; (24)
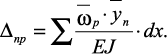
где ω – площадь одной из эпюр изгибающих моментов;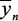 
– ордината другой (обязательно прямолинейной) эпюры, взятой по центру тяжести эпюры ω.
Коэффициенты δnn всегда положительны, коэффициенты δin и свободные
члены Δnp могут быть как положительными, так и отрицательными, а также
равными нулю. Для определения коэффициентов при неизвестных и свободных
членов уравнения необходимо построить «единичные» эпюры изгибающих
моментов: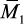 
– от силы x1 = 1; 
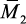– от силы x2 = 1 и т.д. Необходимо построить эпюру Мр от действия на основную систему заданных нагрузок.
Определив коэффициенты при неизвестных и свободные члены
канонических уравнений, приступают к решению системы канонических
уравнений, из которой определяют значения неизвестных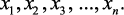 
После определения неизвестных можно приступить к построению
окончательной эпюры изгибающих моментов M. Это может быть осуществлено
с помощью одного из следующих приемов.
Прием первый. Ординаты эпюр от единичных воздействий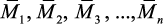 
умножить соответственно на числовые значения
найденных неизвестных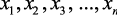 
с учетом знаков (т.е. построить эпюры 
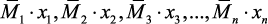). Построить эпюру М путем сложения соответствующих ординат эпюр 
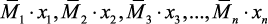с эпюрой изгибающих моментов от внешней нагрузки Mp
Прием второй. Приложить к основной системе заданные нагрузки, найденные усилия (с учетом знака) и построить эпюру М как для обычной статически определимой системы.
Эпюра поперечных сил строится с помощью эпюры изгибающих моментов. Если последняя прямолинейна, то поперечная сила определяется по выражению:
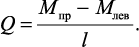
На участках, где данная эпюра криволинейная, эпюра поперечных сил вычисляется по формуле:
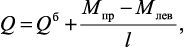
где Qб – «балочная» поперечная сила, которая рассчитывается для данного сечения как для простой балки на двух шарнирных опорах; Mпр– момент на правом конце рассматриваемого участка; Mлев– момент на левом конце рассматриваемого участка; l – длина рассматриваемого стержня.