Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Лекция 14. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Понятие о сложном сопротивлении, его виды. Изгиб с растяжением. Косой изгиб.
Cложное сопротивление – такие виды нагружения бруса, при которых в поперечных сечениях возникают одновременно не менее двух внутренних силовых факторов.
Случаи сложного сопротивления условно разделяют на два вида. Первый вид составляют случаи сложного сопротивления, при которых в опасных точках бруса напряженное состояние является одноосным. В эту группу объединяют: изгиб с растяжением, косой изгиб, внецентренное растяжение-сжатие и др.

Рис. 41. Изгиб с растяжением
Условие прочности при изгибе с растяжением, пренебрегая действием поперечных сил, имеет вид:
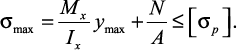 (32)
(32)
Ко второй группе относятся такие случаи сложного сопротивления, когда напряженное состояние является плоским. Например, изгиб с кручением, растяжение(сжатие) с кручением и т.д. Для случая нагружения, относящегося к первой группе, в отличие от второй группы, нет необходимости в применении гипотез прочности.
Косой изгиб проявляется, если прикладываем к балке вертикальную нагрузку, и она при этом изгибается не только в вертикальной плоскости, но и вбок. Косой изгиб – это изгиб, при котором изогнутая ось стержня не лежит в силовой плоскости. Косой изгиб невозможен для балок с сечениями, у которых все центральные оси являются главными (например, квадрат, круг).
Рассмотрим консольную балку прямоугольного сечения длиной l, нагруженную вертикальной силой P. Главная центральная ось балки (ось симметрии) y составляет некоторый малый угол α с направлением действия нагрузки.
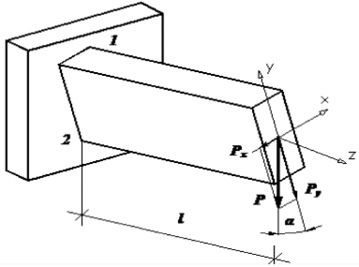
Рис. 42. Косой изгиб
Разложим силу P на составляющие: Py = cos α, Px = sin α . Используя принцип независимости действия сил Py, рассмотрим отдельно действие каждой составляющей. Нагрузки Py и Px вызывают в поперечном сечении, расположенном на некотором расстоянии z от правого конца балки, изгибающие моменты:
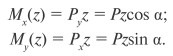
Оба изгибающих момента будут наибольшими в жесткой заделке:
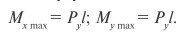
Формула суммарных нормальных напряжений при косом изгибе в произвольном поперечном сечении балки для некоторой точки с координатами x и y:
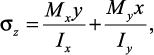 (33)
(33)
где 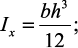
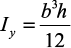 – главные моменты инерции; h – высота, а b – ширина прямоугольного
поперечного сечения балки. Величины изгибающих моментов и координат
данной точки подставляются в формулу нормальных напряжений при косом
изгибе, знак каждого из слагаемых определяется по физическому смыслу.
– главные моменты инерции; h – высота, а b – ширина прямоугольного
поперечного сечения балки. Величины изгибающих моментов и координат
данной точки подставляются в формулу нормальных напряжений при косом
изгибе, знак каждого из слагаемых определяется по физическому смыслу.
Наибольшие нормальные напряжения при косом изгибе возникнут в поперечном сечении, расположенном в жесткой заделке, в наиболее удаленных от соответствующих нейтральных осей точках 1 и 2: y = h/2, x = b/2. В точке 1 напряжения будут растягивающими:
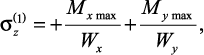
а в точке 2 – такими же по величине, но сжимающими.
В формулах максимальных нормальных напряжений при косом изгибе 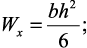
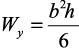 – осевые моменты сопротивления балки относительно главных центральных осей инерции.
– осевые моменты сопротивления балки относительно главных центральных осей инерции.
Нейтральная линия – это геометрическое место точек поперечного сечения стержня, в которых нормальные напряжения равны нулю.
Из определения нейтральной линии легко находится положение нейтральной линии, приравнивая правую часть выражения 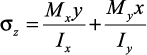 к нулю:
к нулю:
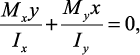
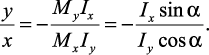
При косом изгибе условие прочности имеет вид:
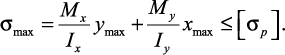 (34)
(34)
Косой изгиб опасен тем, что при производственном браке (перекосе) могут существенно увеличиться нормальные напряжения в балке.