Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Лекция 15. ВНЕЦЕНТРЕННОЕ СЖАТИЕ
Внецентренное сжатие. Построение ядра сечения. Изгиб с кручением. Расчеты на прочность при сложном напряженном состоянии.
Внецентренное сжатие – это вид деформации, при котором продольная сила в поперечном сечении стержня приложена не в центре тяжести. При внецентренном сжатии, помимо продольной силы (N), возникают два изгибающих момента (Mx и My).
Считают, что стержень обладает большой жесткостью на изгиб, чтобы пренебречь прогибом стержня при внецентренном сжатии.
Преобразуем формулу моментов при внецентренном сжатии 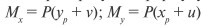 , подставляя значения изгибающих моментов:
, подставляя значения изгибающих моментов:
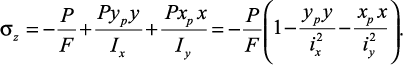
Обозначим координаты некоторой точки нейтральной (нулевой) линии при внецентренном сжатии xN, yN и подставим их в формулу нормальных напряжений при внецентренном сжатии. Учитывая, что напряжения в точках нейтральной линии равны нулю, после сокращения на P/F, получим уравнение нейтральной линии при внецентренном сжатии:
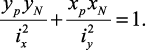 (35)
(35)
Нулевая линия при внецентренном сжатии и точка приложения нагрузки всегда расположены по разные стороны от центра тяжести сечения.
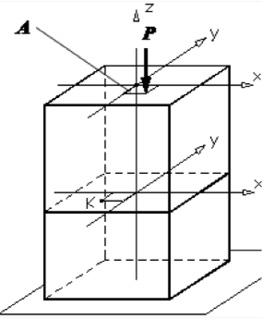
Рис. 43. Внецентренное сжатие
Отрезки, отсекаемые нулевой линией от осей координат, обозначенные ax и ay, легко найти из уравнения нулевой линии при внецентренном сжатии. Если сначала принять xN = 0, yN = ay, а затем принять yN = 0, xN = ax, то найдем точки пересечения нулевой линии при внецентренном сжатии с главными центральными осями:
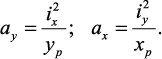
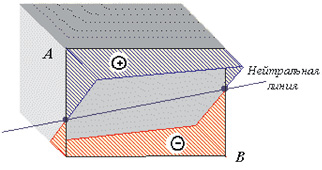
Рис. 44. Нейтральная линия при внецентренном растяжении – сжатии
Нейтральная линия при внецентренном сжатии разделит поперечное сечение на две части. В одной части напряжения будут сжимающими, в другой – растягивающими. Расчет на прочность, как и в случае косого изгиба, проводят по нормальным напряжениям, возникающим в опасной точке поперечного сечения (наиболее удаленной от нулевой линии).
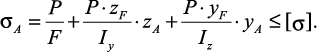 (36)
(36)
Ядро сечения – малая область вокруг центра тяжести поперечного сечения, характерная тем, что любая сжимающая продольная сила, приложенная внутри ядра, вызывает во всех точках поперечного сечения сжимающие напряжения.
Примеры ядра сечения для прямоугольного и круглого поперечных сечений стержня.
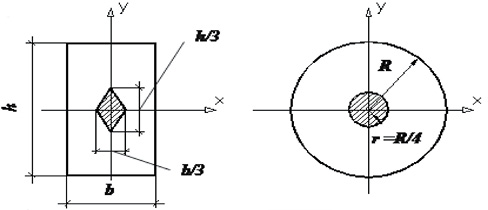
а б
Рис. 45. Форма ядра сечения для прямоугольника и круга
Изгиб с кручением. Такому нагружению (одновременному действию крутящих и изгибающих моментов)часто подвержены валы машин и механизмов. Для расчета бруса необходимо прежде всего установить опасные сечения. Для этого строятся эпюры изгибающих и крутящих моментов.
Используя принцип независимости действия сил, определим напряжения, возникающие в брусе отдельно для кручения, и для изгиба.
При кручении в поперечных сечениях бруса возникают касательные
напряжения, достигающие наибольшего значения в точках контура сечения 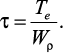 При изгибе в поперечных сечениях бруса возникают нормальные напряжения,
достигающие наибольшего значения в крайних волокнах бруса
При изгибе в поперечных сечениях бруса возникают нормальные напряжения,
достигающие наибольшего значения в крайних волокнах бруса 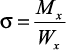 .
.
Касательные напряжения значительно меньше напряжений от крутящего момента, поэтому ими пренебрегают. Опасное сечение бруса будет у заделки, где действуют максимальные напряжения от изгиба и кручения.
Исследуем напряженное состояние в наиболее опасной точке A (рис. 46). Так как напряженное состояние двухосное, то для проверки прочности применяем одну из гипотез.
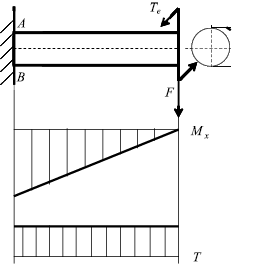
Рис. 46. Эпюры изгибающих и крутящих моментов
Применяя третью теорию прочности
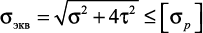
и учитывая, что 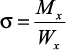 и
и 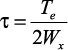 , получаем:
, получаем:
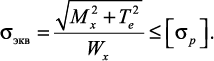
Для подбора сечения находим требуемый момент сопротивления