Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Лекция 17. УДАРНЫЕ НАГРУЗКИ
Основы расчетов на ударное нагружение. Динамический коэффициент. Случаи удара при простейших деформациях.
Явление удара получается в том случае, когда скорость рассматриваемой части конструкции или соприкасающихся с ней частей изменяется в очень короткий период времени.
Таким образом, в ударяемой части конструкции возникают такие напряжения, как будто к ней была приложена сила инерции ударяющего тела; мы можем вычислить эти напряжения, рассматривая силу инерции PД как статическую нагрузку нашей конструкции. Затруднение заключается в вычислении этой силы инерции. Продолжительности удара, т.е. величины того промежутка времени, в течении которого происходит падение скорости до нуля, мы не знаем. Поэтому остается неизвестной величина ускорения, а стало быть, и силы PД. Таким образом, хотя вычисление напряжений при ударе представляет собой частный случай задачи учета сил инерции, однако для вычисления силы PД и связанных с ней напряжений и деформаций здесь приходится применять иной прием и пользоваться законом сохранения энергии.
Применяя закон сохранения энергии, надо:
1) вычислить кинетическую энергию ударяющего тела Т;
2) вычислить потенциальную энергию UД тел, воспринимающих удар, под нагрузкой их силами инерции при ударе; потенциальная энергия должна быть выражена через напряжение (σД, τД,) в каком-либо сечении, через деформацию (удлинение, прогиб) или через силу инерции PД ударяющего тела;
3) приравнять величины потенциальной и кинетической энергий и из полученного уравнения найти или непосредственно динамическое напряжение, или деформацию, а по ней, пользуясь законом Гука, напряжение или силу PД и соответствующие ей динамические напряжения и деформации.
При ударе происходит очень быстрое превращение одного вида энергии в другой: кинетическая энергия ударяющего тела превращается в потенциальную энергию деформации. Выражая эту энергию в функции силы PД или напряжений, или деформаций получаем возможность вычислить эти величины.
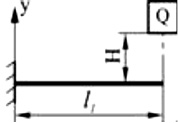
Рис. 53. Модель поперечного удара
Полагая, что кинетическая энергия ударяющего тела полностью переходит в потенциальную энергию деформации упругой системы, можем написать:
T = UД. (38)
Так как к моменту окончания деформации ударяющее тело пройдет путь H + δД, то его запас энергии будет измеряться произведенной им работой AД и будет равен:
T = AД = Q(H + δД).
Вид формулы для UД при ударе примем тот же, что и при статическом нагружении системы С силой инерции PД, т. е.
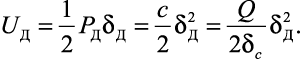
Подставляя значения Т и UД в уравнение (38), получаем:
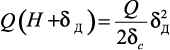
или
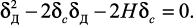
Отсюда
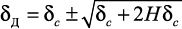 или
или 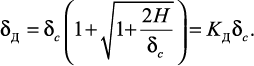
Обозначив T0 = QH – энергия ударяющего тела к моменту начала удара, выражение для динамического коэффициента может быть представлено еще и в таком виде:
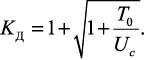 (39)
(39)
Описанный общий прием расчета на удар предполагает, что вся кинетическая энергия ударяющего тела целиком переходит в потенциальную энергию деформации упругой системы. Это предположение не точно. Кинетическая энергия падающего груза частично превращается в тепловую энергию и энергию неупругой деформации основания, на которое опирается система.
Вместе с тем при высоких скоростях удара деформация за время удара не успевает распространиться на весь объем ударяемого тела и в месте удара возникают значительные местные напряжения, иногда превосходящие предел текучести материала.
Динамические напряжения при изгибе балки зависят от модуля упругости материала, объема балки, формы ее поперечного сечения, а также от схемы нагружения и условий опирания балки.