Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Лекция 18. ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ
Основные задачи динамики.
Расчет балок и рам с сосредоточенными массами, имеющих несколько динамических степеней свободы на нагрузку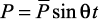 
(или 
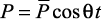) обычно состоит из решения трех задач динамики.
1. Расчет на собственные колебания (1-я задача динамики) состоит из определения частот и форм собственных колебаний динамической системы. Для этого необходимо:
– выбрать расчетную схему и массовую модель сооружения;
– определить степени свободы сосредоточенных масс и их число n;
– определить величины масс, участвующих в колебаниях по каждой степени свободы и построить диагональную матрицу масс m; для системы с двумя степенями свободы она имеет вид
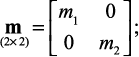
– рассмотреть единичные загружения от воздействия единичных сил;
– во всех единичных загружениях построить эпюры моментов;
– вычислить податливости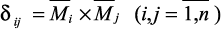 
и построить квадратную матрицу податливости δ; для системы с двумя степенями свободы она имеет вид
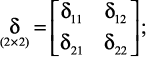
– решить вековое уравнение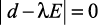 
(где d = δm – динамическая матрица; E – единичная матрица) и вычислить
собственные значения λi, затем круговые частоты собственных колебаний
ωi; при необходимости можно определить формы собственных колебаний ai.
Для системы с одной динамической степенью свободы круговую (циклическую) частоту собственных колебаний можно определять по одной из формул:
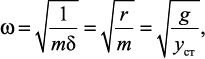(40)
где m – величина сосредоточенной массы; δ, r – податливость и жесткость в направлении степени свободы; g – ускорение свободного падения; yст ? статический прогиб точки от действия веса сосредоточенной массы.
2. Проверка на резонанс (2-я задача динамики) состоит из проверки условий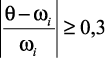 
.
Если во всех случаях результат ≥ 0,3, то резонанса нет и можно
ограничиться расчетом на статическое воздействие нагрузки; если хотя бы
в одном случае результат < 0,3, то динамический расчет надо
продолжить.
3. Проверка динамической прочности (3-я задача динамики) состоит из проверки условия прочности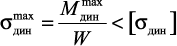 
.
При длительном воздействии вибрационной нагрузки (»107 циклов) за
допустимое динамическое напряжение принимается доля допустимого
статического напряжения: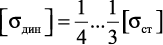 
.
Для построения динамической эпюры моментов Mдин необходимо:
– построить вектор амплитуд действующей на массы нагрузки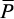 
;
– пользуясь единичными эпюрами от единичных загружений, построить грузовую эпюру MP от вектора нагрузки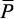 
;
– вычислить все коэффициенты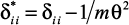 
;
– вычислить вектор статического прогиба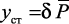 
;
– решить систему канонических уравнений расчета на вибрационную нагрузку; для системы с двумя степенями свободы эта система уравнений имеет вид:
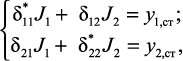
из которой определяются максимальные инерционные силы J1, J2;
– определить обобщенные силы Qi = Pi – Ji;
– построить эпюру динамических моментов от действия обобщенных сил Qi по формуле
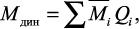
из которой определить значение максимального момента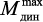 
и затем проверить условие прочности.
Для системы с одной динамической степенью свободы эпюру динамических моментов можно строить по формуле
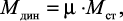(41)
где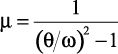 
– динамический коэффициент.
4. Проверка динамической жесткости (4-я задача динамики) решается при необходимости. Она состоит в проверке условия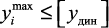 
. Максимальные перемещения по направлениям степеней свободы масс при их колебаниях вычисляются по формуле
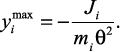
Затем динамическая жесткость проверяется по таблицам, где даны предельные значения допустимых амплитуд вибраций.