Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.1. Постановка задачи математического моделирования процессов переноса при получении УВНМ
Рассмотрим общий случай реализации процесса получения УВНМ. Слой катализатора, известной массой и состава, находится неподвижно на подложке, расположенной в реакционной зоне, с известными геометрическими характеристиками. Любым доступным способом реакционная зона нагрета до требуемой температуры. Поток углеводорода, подаваемого с известным расходом и начальной температурой, движется над слоем катализатора. Эскиз объекта математического моделирования представлен на рис. 3.1.
Состав и структура взаимосвязей определяющих процессов получения УВНМ представлена во второй главе.
Применение системного подхода к решению задачи математического моделирования процессов получения УВНМ преодолевает высокую размерность. Таким образом, декомпозиция сложной изначальной задачи компенсируется взаимоувязки частных решений, при этом изначальная задача перестает быть неразрешимой и сводится к продолжительности расчета, а в итоге – к эффективности вычислительных средств.
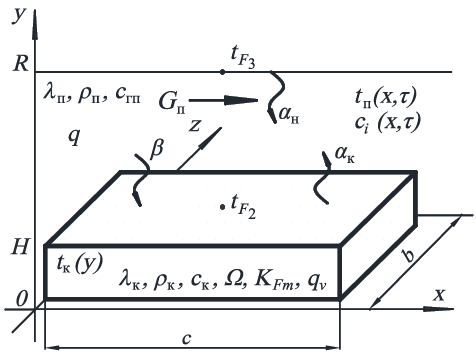
Рис. 3.1. Эскиз реакционной зоны с указанием определяющих параметров
Частными решениями каждого блока второго уровня задачи (2.1)–(2.16) являются функциональные зависимости:
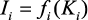, i = 1..6. (3.1)
Таким образом, общая постановка задачи математического моделирования процессов получения углеродных наноматериалов имеет вид:
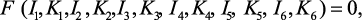(3.2)
необходимо найти fi и F, что бы выражение (3.2) обращалось в тождество.
Представляется целесообразным, наряду с системным анализом, применение методологии, реализующую представление полей определяющих параметров процессов, как совокупность полей элементарных областей, моделируемых аналитическими решениями систем линейных дифференциальных уравнений, описана в [239].
Представлена система допущений, позволяющая решить поставленную задачу математического моделирования процессов получения УВНМ с достаточной степенью достоверности, необходимой для выполнения инженерных расчетов:
1. Значения физических и физико-химических характеристик внутри локальной области постоянны.
2. Процессы переноса квазистационарные с распределенными параметрами и дискретизацией по времени.
3. Газовый поток движется в поршневом режиме.
4. Потери тепла в окружающую среду пренебрежимо малы.
5. Слой катализатора рассматривается как единая система с интегральными значениями физических параметров.
Использование допущения 3 позволяет упростить, без искажения механизмов процесса, решение общей задачи моделирования процесса и исключить из рассмотрения градиент скорости потока в реакционной зоне.