Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

РАЗРАБОТКА ТЕОРЕТИЧЕСКОЙ МОДЕЛИ ОЦЕНКИ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ В РАМКАХ ПЛАЗМОПОДОБНОЙ КОНЦЕПЦИИ РАСТВОРОВ ЭЛЕКТРОЛИТОВ

Танганов Б Б, Бубеева И А, Багаева Т В,

1.2. Методы экспериментального определения и расчета коэффициента теплопроводности водных растворов электролитов

В работах Л. Риделя [20–22] водные растворы электролитов рассматриваются как многокомпонентные системы, состоящие из молекул воды, катионов и анионов соли. В этих работах предполагается, что катионы и анионы соли изменяют теплопроводность растворителя (воды) независимо друг от друга. Тем самым, величина изменения теплопроводности растворителя (воды) определяется алгебраической суммой соответствующих значений теплопроводности, приходящихся на катион (Kt+) и анион (An–).

Ридель в своих работах [20–22] приводит данные по теплопроводности водных растворов солей некоторых металлов, а также нескольких кислот и оснований, полученные методом коаксиальных цилиндров при атмосферном давлении, температурах до 20 °С (для NaOH и KOH до 80 °С) и массовых долях вещества до 0,5.

Для расчета же теплопроводности водных растворов солей при 20 °С им была предложена следующая формула, подтверждающая экспериментально полученные данные:

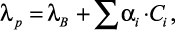(1.4)

где λp –	коэффициент теплопроводности водного раствора электролита;
λB –	коэффициент теплопроводности воды;
αi –	коэффициент, характеризующий изменение теплопроводности раствора;
Ci –	мольная концентрация соли, моль/л.

Величина 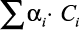изменяется в зависимости от числа n анионов и m катионов. Значения коэффициента αi для различных ионов определялись по экспериментальным данным по теплопроводности водных растворов электролитов.

Теплопроводность раствора при разных температурах можно рассчитать по эмпирической формуле:

λp = λB⋅f(t), (1.5)

где f(t) – температурный коэффициент.

Значения величин λB, αi и f(t) приведены в работах [20–22]. При этом за начало отсчета для всех ионов принято значение αNa = 0.

Большое внимание в работах [20–22] уделено изучению теплопроводности водных растворов NaOH и KOH, для описания свойств которых Риделем была предложена следующая формула:

λp = λB + α⋅C + φ(C), (1.6)

где α –	коэффициент, учитывающий ионы натрия или калия;
φ(C) –	эмпирическая концентрационная зависимость.

Авторами [23–25] были обнаружены существенные расхождения между экспериментально найденными и вычисленными по формуле (1.4) значениями теплопроводности некоторых растворов электролитов.

В работе [25] указывается, что в ряде случаев формула (1.4) дает искаженные результаты. Так, например, вычисленные значения теплопроводности водных растворов фторида и бромида натрия значительно меньше экспериментальных. Автор [25] объясняет эти расхождения отсутствием при составлении таблицы коэффициентов αi экспериментальных данных по теплопроводности в области сильно разбавленных растворов, недостаточным объемом и сочетанием катионов и анионов исследуемых солей, а также заданием нулевого значения αi и изменением теплопроводности воды для катиона натрия.

Черненькая Е.И. и Вернигора Г.А. [26] модифицировали уравнение Риделя:

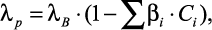(1.7)

где λp и λB в Вт/(м⋅К); Ci – концентрация компонента, кг вещества на 1 кг раствора; βi – коэффициенты, полученные путем математической обработки экспериментальных данных по теплопроводности ряда неорганических веществ.

По выражению (1.7) рассчитывается теплопроводность многокомпонентных растворов электролитов при атмосферном давлении в интервале температур 293–373 К.

В те годы изучению теплопроводности воды был посвящен ряд работ. Так, в работе [27] аппроксимирована зависимость теплопроводности воды от температуры:

λB = 0,5545 + 0,00246⋅t – 0,00001184⋅t2. (1.8)

В середине 50-х гг. Капустинский А.Ф. и Рузавин И.И.
[28–31] исследовали теплопроводность различных водных растворов электролитов методом плоского слоя при температуре 25 °С и атмосферном давлении. Авторами [28–31] было введено понятие «кажущейся» молярной теплопроводности φK и получено выражение для ее расчета:

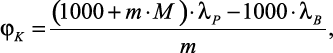(1.9)

где m –	молярная концентрация раствора электролита;
M –	мольная масса соли.

Рассчитав по экспериментально полученным данным значения φK для различных концентраций и анализируя эти зависимости, которые в координатах φK – m представляют прямые линии, авторы составили таблицу «кажущихся» значений теплопроводности ионов φK при 25 °С и их гидратированных радиусов при бесконечном разбавлении солей. Зная значение φK, по формуле (1.9) можно вычислить теплопроводность раствора.

В работе [25] проведен анализ формул (1.4) и (1.9), в которой автором установлено, что в некоторых случаях вычисленные значения не согласуются с экспериментально полученными. Автор [25] считает причиной этих расхождений различное влияние An– и Kt+ на теплопроводность воды в широком диапазоне концентраций. Им предложено для разделения коэффициента теплопроводности растворов на отдельные составляющие использовать фтористый калий. Это объясняется тем, что кристаллографические радиусы ионов калия и фтора одинаковы (ri = 0,133 нм) и близки к радиусу молекулы воды (ri = 0,138 нм), а кроме того энергии гидратации этих ионов практически равны между собой (60 и 61 кДж/моль соответственно). Поэтому при растворении следует ожидать равного влияния ионов калия и фтора на теплопроводность воды. Кроме этого в работе [54] предложен другой способ разделения теплопроводности растворов, в котором в качестве стандарта использована соль NaCl. Результаты получились идентичными. Анализируя исследования Риделя [20–22] и Капустинского А.Ф. и Рузавина И.И. [28–31], автор [25] отмечает, что работа не доведена до логического конца. Видимо, следовало бы с единых позиций переработать весь имеющийся экспериментальный материал с целью получения новых значений коэффициента для всех исследованных электролитов (ионов).

Варгафтик Н.Б. и Осьминин Ю.П. [32–35] исследовали теплопроводность водных растворов некоторых солей, кислот и оснований при температуре 20 °С и атмосферном давлении. Для исследований был использован метод нагретой нити.

Для расчета теплопроводности водных растворов солей, кислот и щелочей автор [36] предложил использовать следующую формулу:

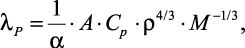(1.10)

где α –	фактор, учитывающий степень ассоциации;
A –	величина, являющаяся функцией температуры независимо от рода жидкости;
ρ –	плотность раствора электролита;
Cp –	теплоемкость при постоянном давлении.

Полагая, что коэффициенты ассоциации для воды и раствора равны, в [32–35] получили следующее выражение для коэффициента теплопроводности растворов электролитов:

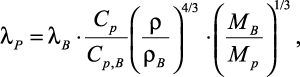(1.11)

где Cp, Cp,B –	изобарная теплоемкость соответственно раствора электролита и воды;
ρB –	плотность воды;
Mp, MB –	мольные массы соответственно раствора электролита и воды.

В свою очередь мольная масса раствора электролита определяется по формуле [32–35]:

Mp = MB·NB + M·N, (1.12)

где NB, N – мольная концентрация воды и электролита.

Расчет теплопроводности раствора электролита по представленной формуле затрудняется, если отсутствуют значения теплоемкости Cp и плотности ρ раствора электролита данной кон-
центрации.

Миснар [24] для расчета теплопроводности водных растворов элементов первой и второй групп периодической системы при 20 °С представил формулу, в которой в определенной степени учитываются молекулярные характеристики растворенного вещества:

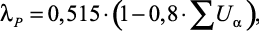(1.13)

где λp в ккал/(м⋅час⋅град); 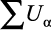– суммарная объемная концентрация растворенных солей.

Ошибка расчета λp по (1.13) составляет не менее 3 %, если член 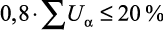, что соответствует массовым концентрациям 30–40 %.

При отсутствии значений объемов или плотностей рассматриваемых растворов коэффициент теплопроводности раствора соли рассчитывается по выражению:

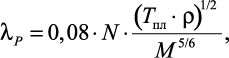(1.14)

где N –	число атомов в молекуле соли;
Tпл –	температура плавления соли.

В работе [37] авторы предложили следующую формулу:

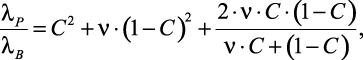(1.15)

где 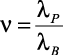; С – параметр, связанный с объемной концентрацией P2 растворенного компонента следующим соотношением

P2 = 2C3 – 3C2 + 1. (1.16)

Коэффициент теплопроводности λP по [38] может вычисляться как

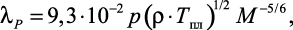(1.17)

где p – число атомов в молекуле соли.

В последующие годы было выполнено несколько экспериментальных работ по теплопроводности водных растворов электролитов. Так, например, в работе [39] были выполнены исследования методом нагретой нити при температурах до 40 °С и атмосферном давлении в интервале концентраций 0,09–2,25 моль/кг. В середине 70-х гг. в работах [40–41] изучали теплопроводность хлорида натрия методом плоского слоя в интервале температур 20–330 °С при давлениях до 20 МПа.

В работе [42] описывается прибор для определения теплопроводности воды, использующий метод плоского горизонтального слоя. Коэффициент теплопроводности авторами вычисляется по формуле:

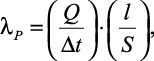(1.18)

где Q –	тепловой поток, Вт;
Δt –	перепад температуры в слое, °С;
l –	толщина плоского слоя, м;
S –	расчетная поверхность, м2.

На основе экспериментальных данных в работе [42] было получено уравнение, описывающее значения теплопроводности воды в зависимости от температуры:

λB = (0,007·t3 – 9,38·t2 + 2114,1·t + 556536)·10–6. (1.19)

Рекомендуемые авторами значения λB имеют хорошее согласие с работами других авторов, лишь при температурах, близких к 350 °С, расхождения доходят до 3 %.

Груздевым В.А. с сотрудниками [43] были проведены измерения теплопроводности концентрированных растворов хлорида натрия методом коаксиальных цилиндров в диапазоне температур 21–92 °С и атмосферном давлении. Основные выводы и результаты исследований заключаются в констатации качественной идентичности температурных зависимостей воды и раствора, а также в том, что изотермы концентрационных зависимостей не являются прямыми линиями.

За рубежом также проводились исследования водных растворов некоторых электролитов. В частности, известны работы японских исследователей [44–47] по теплопроводности водного раствора хлорида натрия.

В 1988 году в работах [48–49] были опубликованы «выравненные» значения теплопроводности водных растворов веществ, полученных путем машинной обработки справочных данных. При обработке значений теплопроводности использовалась
зависимость:

λP = λB·h·exp(ν + δ·t)·t, (1.20)

где t –	температура;
h, ν и δ –	искомые коэффициенты пропорциональности.

Для растворов наиболее широко применяемых неорганических веществ проводили экстраполяцию теплопроводности в области температур от 90 до 200 °С по зависимости (1.20). Полученные экстраполированные данные следует рассматривать как прогнозируемые.

В этом направлении проводилась еще одна работа, которую хотелось отметить. Авторами [50] с использованием имеющихся в литературе данных составлены таблицы плотности, теплоемкости, кинематической вязкости, критерия Прандтля, коэффициентов температуропроводности и теплопроводности для водных растворов некоторых солей в диапазоне концентраций от 5 % до 15–60 % для различных растворов и от 20 °С до температур кипения при атмосферном давлении. Для получения значений свойств в указанных интервалах температур и концентраций по ограниченным данным использовались сравнительные методы. Для расчета значений плотности, коэффициентов температуропроводности и теплопроводности были получены зависимости, имеющие единую форму:

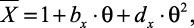(1.21)

где –

приведенное значение одной из указанных характеристик x при температуре t, °C;

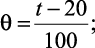
bx, dx –

коэффициенты, имеющие определенные значения для каждой из характеристик (например, плотности).

При использовании сравнительных методов в качестве стандартной жидкости принимались растворитель (вода) или раствор электролита, для которого искомое свойство известно в более широком интервале параметров.

В последние годы наметилась тенденция исследования водных растворов электролитов в широких интервалах температур и давлений.

Широкие исследования по теплопроводности бинарных растворов были проведены в Грозненском нефтяном институте Расторгуевым Ю.Л. и Ганиевым Ю.А. и их последователями [51–61].

В работах [51–53] Расторгуевым Ю.Л. и Ганиевым Ю.А. было предложено уравнение для расчета теплопроводности водных растворов электролитов:

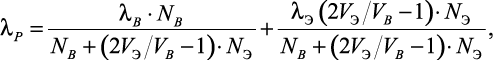(1.22)

где VB, NB –	мольный объем и концентрация в мольных долях воды;
λЭ, VЭ –	коэффициент теплопроводности и мольный объем соли при температуре раствора;
NЭ –	концентрация соли в мольных долях.

При этом предполагается, что

VЭ = VA·NA + VK·NK, (1.23)

где VA, VK –	молекулярные объемы анионов и катионов;
NA, NK –	количество анионов и катионов в одном моле соли.

Авторами [51–55] была подробно изучена теплопроводность воды и водных растворов хлорида натрия при давлениях до 100 МПа и температурах до 400 °С.

Расторгуев Ю.Л., Ганиев Ю.А., Сафронов Г.А и Григорьев Е.Б. [58–61] изучали теплопроводность водных растворов фторидов лития и натрия и бромида натрия в диапазоне температур
20–200 °С, давлении 0,5–100 МПа методом коаксиальных цилиндров.

Сафронов Г.А. [25, 60–61] методом коаксиальных цилиндров исследовал теплопроводность водных растворов NaF и NaBr в интервале температур 20–180 °С и LiF – 25–30 °С и давлений
0,5–100 МПа. Исследованный диапазон концентраций изменялся от 0,00071 до 0,0291 мол.дол.

Автор [34] использовал уравнение:

ai = γi·Ni, (1.24)

где ai –	активность;
γi –	коэффициент активности;
Ni –	концентрация в мольных долях.

Величина ai отражает взаимодействие между частицами в растворе и определяется экспериментальным путем [25].

Таким образом, Сафронов в работе [25] показал, что зависимость коэффициента теплопроводности раствора от активностей воды и электролита имеет вид:

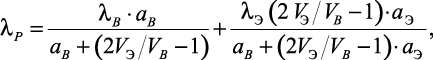(1.25)

где AB –	активность воды в растворе;
aЭ –	активность электролита.

Эльдаров В.С. с сотрудниками [62–68] исследовали теплопроводность водных растворов индивидуальных галогенидов элементов первой и второй групп периодической системы в интервале температур 20–200 °С при давлениях 0,1–30 МПа и массовых долях вещества до 0,5. Измерения выполнены методом коаксиальных цилиндров. В работах [62–68] представлены эмпирические зависимости теплопроводности водных растворов электролитов от концентрации, температуры и давления. Теплопроводность в зависимости от концентрации определяется по формуле:

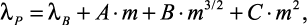(1.26)

где m –	мольная концентрация раствора электролита;
A, B, C –	эмпирические коэффициенты.

Уравнение (1.26) для расчета температурной зависимости теплопроводности водных растворов электролитов преобразовано авторами в выражения:

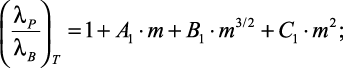(1.27)

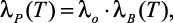(1.28)

где A1, B1, C1 –	эмпирические коэффициенты, независящие от температуры;
λо –	относительная теплопроводность при начальной температуре Tо и заданной концентрации.

Последнюю формулу авторами рекомендуется использовать для приближенных расчетов коэффициентов теплопроводности до температуры 300 °С.

Эльдаровым В.С. в работах [62–68] установлено, что при давлении 0,1–30 МПа относительная теплопроводность 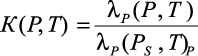не зависит от рода электролита, что позволило автору предложить эмпирическую формулу для расчета λP бинарных растворов при различных концентрациях m, температурах T и давлениях P:

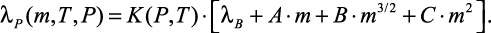(1.29)

Магомедов У.Б. [69–71] методом плоского слоя исследовал теплопроводность водных растворов различных солей в интервалах температур 20–200 °С, давлений 0,1–100 МПа и массовых долей вещества 0,025–0,25. Для описания экспериментальных данных в исследованных интервалах автор [69–70] предложил две расчетные формулы. Первая формула описывает зависимость коэффициента теплопроводности от температуры, давления
и концентрации:

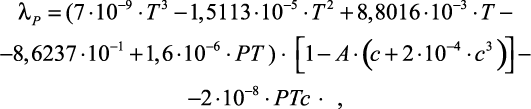(1.30)

где c –	массовая доля вещества, %;
A –	коэффициент, характерный для каждой системы электролита.

Численные значения коэффициента A представлены в работах [69–70].

Вторая формула связывает коэффициент теплопроводности водных растворов электролитов с плотностью при различных температурах, давлениях и концентрациях:

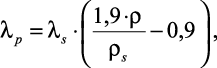(1.31)

где λs и ρs –

соответственно теплопроводность вблизи линии насыщения и плотность на линии насыщения.

В работе [71] представлена формула, позволяющая получить расчетные данные о теплопроводности электролитов вблизи линии насыщения при температурах 273–533К и массовой доли растворенного вещества 0,1–25 масс. %:

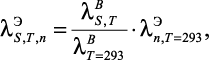(1.32)

где –	коэффициент теплопроводности электролита вблизи линии насыщения при температуре T и молярной концентрации n;
–	коэффициент теплопроводности воды при температуре T вблизи линии насыщения;
–	коэффициент теплопроводности электролита при температуре T = 293 К и молярной концентрации n.

Расчетные данные по теплопроводности водных растворов солей по формуле (1.32) вблизи линии насыщения отклоняются от экспериментальных данных [71] не более, чем на 2 %.

Поскольку в реальных технологических системах применяются многокомпонентные смеси, то актуальными являются исследования теплопроводности этих смесей. Так, например, в работе [101] изучались термодинамические свойства двух- и трехкомпонентных водных растворов галогенидов металлов.

Автором [72] была предложена формула для определения экспериментальных данных водных бинарных растворов электролитов:

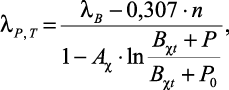(1.33)

где n –	молярная концентрация раствора электролита;
Aχ, Bχ –	эмпирические коэффициенты;
P, P0 –	рабочее и атмосферное давление.

Работа Косолапа Ю.Г. [72] интересна еще и тем, что он исследовал теплопроводность не только бинарных, но и тройных водных растворов галогенидов натрия и калия. Измерения проведены методом коаксиальных цилиндров в интервале температур 20–200 °С и давлений 0,1–100 МПа. Диапазон концентраций составил 0,007–0,07 мол.дол. Для тройных систем суммарные концентрации изменялись в интервале 4,9–31,5 %. В работе [72] впервые экспериментально определены значения теплопроводности смешанных водных растворов галогенидов калия.

Заслуживает внимания предложенный проф. Д.Л. Тимротом [73–74] термоэлектрический стационарный метод определения теплопроводности жидкостей, основанный на использовании эффекта Пельтье. Термоэлектрическая цепь состоит как минимум из двух спаев и помещается в изотермическую среду. Разность температур между спаями, возникающая при прохождении электрического тока, зависит либо от теплопроводности материалов цепи, если теплообмен с окружающей средой мал, либо от теплообмена с окружающей средой, если он превалирует. В условиях неподвижной среды определяющим фактором для теплообмена будет теплопроводность этой среды.

Плечо R3 рис. 1.1 представляет собой 2n-спайную дифференциальную термопару. Плечо R4 является 2-спайной термопарой, изготовленной из тех же материалов, что и R3. Величина разбаланса моста при прохождении через спаи тока будет равна

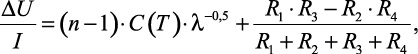(1.34)

где ΔU –	разбаланс с диагонали моста;
I –	сила тока;
n –	число пар спаев;
C(T) –	константа градуировки, зависящая от температуры;
R –	омические сопротивления плеч моста.

Преимуществом данной схемы измерений является то, что, согласно уравнению, число пар спаев не имеет ограничений. Это позволяет увеличивать чувствительность схемы до необходимого уровня простым увеличением числа пар спаев.

Как видно из рассмотренных работ, исследования теплопроводности водных растворов электролитов, в основном, проводились при атмосферном давлении в небольшом интервале температур или при одной температуре. Результаты исследований использовались для проверки и получения эмпирических уравнений расчета теплопроводности водных растворов, а также в прикладных целях. Наибольшее количество экспериментальных работ посвящено исследованию теплопроводности водного раствора хлорида натрия. Кроме него были исследованы растворы еще нескольких электролитов, но их набор не отличался разнообразием.

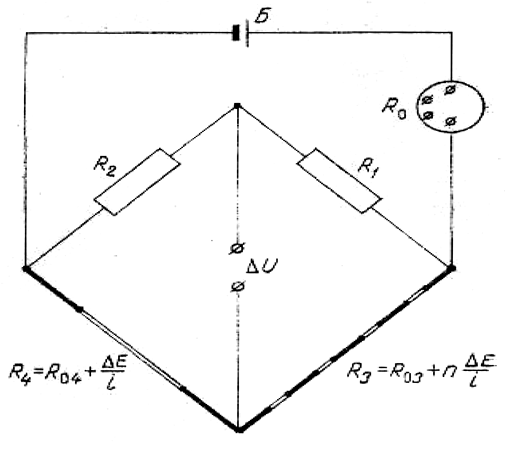
Рис. 1.1. 2n-спайная мостовая схема

Поэтому основной задачей исследования явилось создание модели оценки теплопроводности водных растворов электролитов в широком диапазоне изменения концентраций и температур. Эта модель должна быть независима от экспериментальных значений по теплопроводности водных растворов электролитов.
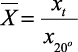
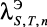
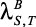
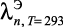