Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Танганов Б Б, Бубеева И А, Багаева Т В,
1.3. Об уравнениях для расчета теплопроводности жидкостей
В современной технике применяются разнообразные жидкости как теплоносители. Однако не всегда имеется возможность своевременно получить экспериментальные данные по физическим свойствам этих веществ. Это особенно относится
к теплопроводности, экспериментальное определение которой представляет значительные трудности. Поэтому важно рассмотреть уравнения, которые являются наиболее надежными и удобными для расчета теплопроводности с достаточным для практики приближением
В настоящее время известен ряд формул для расчета теплопроводности жидкостей.
Механизм распространения теплоты в жидкостях можно представить как перенос энергии путем нестройных упругих колебаний. Такое теоретическое представление о механизме передачи теплоты в жидкостях, выдвинутое А.С. Предводителевым, было использовано Н.Б. Варгафтиком для описания опытных данных по теплопроводности различных жидкостей. Для большинства жидкостей теория нашла хорошее подтверждение. На основании этой теории была получена формула для коэффициента теплопроводности следующего вида:
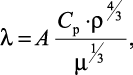(1.35)
|
где Cp – |
теплоёмкость жидкости при постоянном давлении; |
|
ρ – |
плотность жидкости; |
|
μ – |
молекулярная масса |
Коэффициент A, пропорциональный скорости распространения упругих волн в жидкости, не зависит от природы жидкости, но зависит от температуры, при этом A·Cp ≈ const.
Так как плотность ρ жидкости с повышением температуры убывает, то из уравнения (1.35) следует, что для жидкостей с постоянной молекулярной массой (неассоциированные и слабо ассоциированные жидкости) с повышением температуры коэффициент теплопроводности должен уменьшаться. Для жидкостей, сильно ассоциированных (вода, спирты и т.д.) в формулу (1.35) нужно ввести коэффициент ассоциации, учитывающий изменение молекулярной массы. Коэффициент ассоциации зависит также от температуры, и поэтому при различных температурах он может влиять на коэффициент теплопроводности по-разному.
При повышении давления коэффициенты теплопроводности жидкостей возрастают.
Существует формула Крагое, которая приводится во многих руководствах по нефтепродуктам:
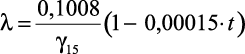ккал/м·ч·°С, (1.36)
|
где λ – |
коэффициент теплопроводности; |
|
γ15 – |
удельный вес при 15 °С, г/см3. |
Сравнение экспериментальных данных с этой расчетной формулой Крагое приводится в статье В.Н. Попова и Е.В. Цеденберга. Оказалось, что для ряда жидкостей при температуре от –40 до + 200 °С значения теплопроводности, вычисленные по формуле (1.36), превышают на 20–40 % экспериментальные данные, что, естественно, исключает возможность пользоваться формулой Крагое даже для предварительных расчетов теплопроводности жидкостей.
Практический интерес представляет обобщенная формула Предводителева-Варгафтика для нормальных и ассоциированных жидкостей:
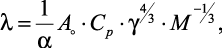ккал/м·ч·°С, (1.37)
|
где α – |
коэффициент, учитывающий степень ассоциации жидкостей (для неассоциированных жидкостей α = 1); |
|
Ao = 1,54 – |
универсальная величина для всех жидкостей при |
|
γ – |
удельный вес в г/см3; |
|
M – |
молекулярный вес; |
|
Cp – |
теплоемкость при |
|
Tкр – |
критическая температура в К (для большинства жидкостей, исключая низкокипящие, |
;
;
).
В работе [14] показано, что для жидкости
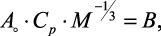(1.38)
– величина постоянная, не зависящая от температуры. Таким образом, для неассоциированных жидкостей:
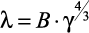ккал/м·ч °С. (1.39)
Уравнение (1.39) позволяет определить зависимость λ от температуры, если известна зависимость γ = f(t).
Уравнения (1.37) и (1.39) проверялись на многих жидкостях несколькими авторами. В результате уравнение (1.37) вполне удовлетворительно согласуется с экспериментальными данными. Разброс не превышает 5 %. Н.В. Цедерберг проверил применимость формулы (1.39) для расчета теплопроводности жидкостей в широком интервале температур. Максимальное расхожде-
ние равно 2,6 %.
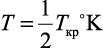
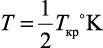
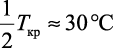