
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.1. Плазмоподобная концепция подвижности ионов в растворах электролитов
Одной из фундаментальных задач теории растворов является задача подвижности ионов и молекул как базисного параметра исследования диссипативных свойств [75–79].
Для системы зарядов выражение для подвижности можно записать в виде соотношения:
 (2.2)
(2.2)
|
где V – |
скорость движения ионов под действием внешней силы F = eE; |
|
E – |
напряженность поля. |
Решение уравнения подвижности ионов в растворах электролитов возможно при наличии значений V и E, которые требуют предварительного определения.
При выводе уравнения скорости движения ионов воспользуемся следующими рассуждениями. В механике полная энергия системы зарядов состоит из суммы кинетической и потенциальной энергий:
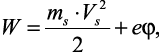 (2.3)
(2.3)
|
где ms – |
массы сольватированных ионов; |
|
Vs – |
скорость их движения; |
|
φ – |
обобщенный потенциал самой системы. |
Убыль полной энергии для системы зарядов можно представить в присутствии внешнего поля в виде работы в едини-
цу времени
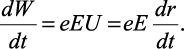 (2.4)
(2.4)
Полная производная этой энергии будет равна
W = eEr + const, (2.5)
|
где E – |
напряженность электрического поля для системы зарядов; |
|
r – |
расстояние или длина свободного пробега. |
Приравняв (2.3) и (2.5), получаем
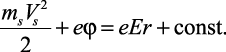 (2.6)
(2.6)
Для данного случая согласно [5] принимаем, что 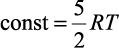 , тогда (2.6) примет вид
, тогда (2.6) примет вид
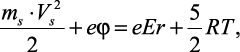 (2.7)
(2.7)
|
где R – |
универсальная газовая постоянная; |
|
T – |
температура. |
Поскольку работа eEr равна убыли электрической энергии, т.е. eEr = –eφ, последнее выражение можно представить как
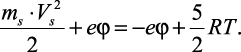 (2.8)
(2.8)
Решая данное уравнение относительно V, получим выражение скорости движения ионов, определяемое для решения проблемы подвижности:
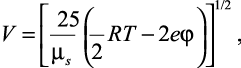 (2.9)
(2.9)
где μs – приведенная масса сольватированных ионов.
Уравнение (2.9) справедливо для сильных, полностью диссоциированных, электролитов. В случаях, когда электролит диссоциирует слабо, необходимо учитывать ионную составляющую электролита, тогда
C = Cобщ·α,
|
где С – |
концентрация электролита; |
|
Cобщ – |
общая концентрация электролита; |
|
α – |
степень диссоциации электролита. |
Кроме того, следует учитывать функцию распределения ионной составляющей по скоростям Максвелла f, полное выражение для определения которой представлено ниже.
Тогда полное уравнение скорости движения ионов может быть представлено следующим образом:
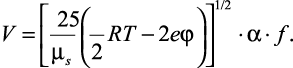 (2.10)
(2.10)
Как видно из (2.2) при решении задачи о подвижности требуется расшифровка напряженности внешнего поля E. Для этого в произвольную точку раствора i введем пробный заряд величиной ei = zie. Потенциал поля в данной точке φi будет равен
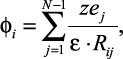 (2.11)
(2.11)
|
где ej = zje – |
заряд любого из ионов, кроме рассматриваемого в точке i; |
|
ε – |
диэлектрическая проницаемость среды; |
|
Rij – |
расстояние между ионами i и j. |
Полная энергия ионов в точке i определяется выражением
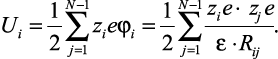 (2.12)
(2.12)
Из (2.12) потенциальную энергию системы зарядов в растворе можно выразить как
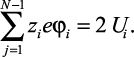 (2.13)
(2.13)
Для учета силы, действующей на ион в точке i со стороны самосогласованного поля остальных ионов, (2.13) умножим на  :
:
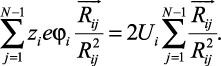 (2.14)
(2.14)
Так как сила, определяемая по (2.14), равна силе внешнего поля eE, получаем следующее выражение:
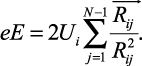 (2.15)
(2.15)
Из (2.12) расстояние между ионами определяется как
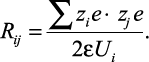 (2.16)
(2.16)
Подставляя Rij в (2.15) и решая уравнение относительно E, получаем выражение для нахождения напряженности внешнего поля:
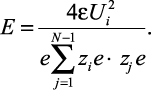 (2.17)
(2.17)
Представим сумму 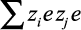 , как
, как 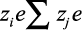 . Из условия электронейтральности
. Из условия электронейтральности 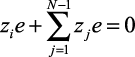 следует, что
следует, что 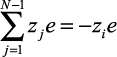 . С учетом этого (2.17) запишется как
. С учетом этого (2.17) запишется как
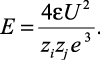 (2.18)
(2.18)
Таким образом, подставив (2.10) и (2.18) в уравнение для нахождения подвижности, (2.2) приобретает вид:
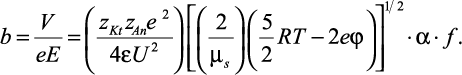 (2.19)
(2.19)
Из уравнения (2.19) видно, что основными составляющими являются энергия межмолекулярных взаимодействий в растворителе U, приведенная масса гидратированных ионов μs и eφ – потенциальная энергия системы зарядов.
Для нахождения потенциальной энергии eφ в выражении (2.19) воспользуемся выражением [87]:
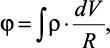 (2.20)
(2.20)
|
где ρ – |
плотность заряда в системе, т.е. количество заряда в единице объема; |
|
V – |
объем сферы; |
|
R – |
расстояние от заряда до рассматриваемой точки поля. |
Исходя из того, что элемент объема dV = 4π2dr имеет сферическую форму, то выражение (2.20) примет вид
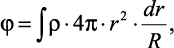 (2.21)
(2.21)
где r – радиус сферы.
Потенциал φ на расстоянии, равном радиусу сферы (R = r), будет равен
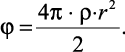 (2.22)
(2.22)
Принимая во внимание, что плотность равняется произведению ρ = ne, где n – плотность числа частиц в 1 мл раствора (в единице объема), и умножая обе части выражения (2.22) на величину e, получим
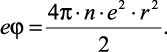 (2.23)
(2.23)
Согласно [88], величина
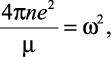 (2.24)
(2.24)
есть квадрат частоты колебаний плотности заряда в плазме [80], где μ – масса несольватированных ионов.
Согласно известной задаче механики [4], выражение (2.24) есть не что иное, как потенциальная энергия одномерного линейного гармонического осциллятора. Такой осциллятор имеет точку поворота (V = 0), где кинетическая энергия равна нулю, а потенциальная энергия максимальна. При прохождении через состояние равновесия кинетическая энергия максимальна, а потенциальная равна нулю.
Отсюда следует, что 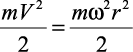 и генератором колебаний является неустойчивость по Ирншоу в точках поворота при V = 0, когда распределение зарядов статическое. Таким образом, основное время ионы проводят именно в окрестностях точки поворота. А это предопределяет обратное движение противоионов с последующей их рекомбинацией в KtAn.
и генератором колебаний является неустойчивость по Ирншоу в точках поворота при V = 0, когда распределение зарядов статическое. Таким образом, основное время ионы проводят именно в окрестностях точки поворота. А это предопределяет обратное движение противоионов с последующей их рекомбинацией в KtAn.
Согласно теореме вириала о средних значениях энергии [4, 6], запишем
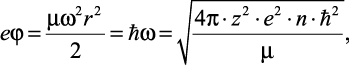 (2.25)
(2.25)
где ћ – постоянная Планка.
Далее, если иметь в виду, что плотность частиц 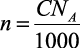 , где C – молярность раствора и NA – число Авогадро, то получим выражение для определения потенциальной энергии:
, где C – молярность раствора и NA – число Авогадро, то получим выражение для определения потенциальной энергии:
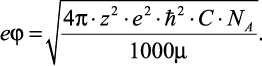 (2.26)
(2.26)
Согласно функции максвелловского распределения по скоростям движения ионов при температуре T ионы обладают кинетической энергией и выражение для определения f имеет вид:
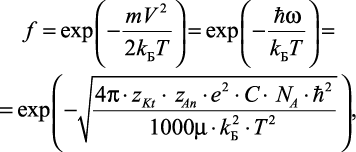 (2.27)
(2.27)
где kБ – постоянная Больцмана.
Подставив (2.26) и (2.27) в (2.19), получим выражение для определения подвижности
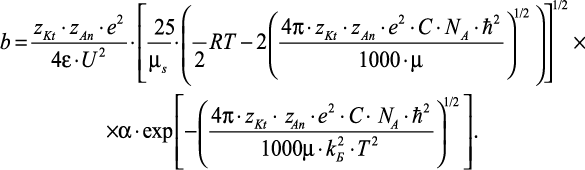 (2.28)
(2.28)
Определение подвижности ионов требует предварительной аппроксимации масс сольватированных ионов μs, энергии межчастичных взаимодействий eφ, степени диссоциации электролита α, энергии межмолекулярных взаимодействий в чистых растворителях U. Полученное уравнение для расчета подвижности ионов используется в модельном выражении для определения теплопроводности водных растворов электролитов.
