Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Танганов Б Б, Бубеева И А, Багаева Т В,
2.2. Сольватные числа, массы и радиусы сольватированных ионов
Кроме величины подвижности ионов в модельном уравнении необходима аппроксимация сольватных чисел и с их использованием – радиусов сольватированных ионов.
Поскольку сольватные числа ионов однозначно не были оценены, а экспериментально определены только их суммы для электролитов с последующим разделением на ионные составляющие с помощью ряда допущений [81–85], то разработке оценочных моделей сольватных чисел придается большое значение.
Заряд иона в жидком диэлектрике экранируется ближайшим окружением из n молекул растворителя, образующих сольватную оболочку. При этом осуществляется ион – дипольное взаимодействие, потенциалы которых равны:
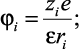
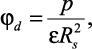(2.29)
|
где zie – |
заряд иона; |
|
p – |
дипольный момент молекулы растворителя; |
|
Rs – |
радиус молекулы растворителя. |
Потенциал центрального иона в диэлектрической среде экранируется дипольным потенциалом φd молекул растворителя (числом сольватированных ионов ns) по принципу суперпозиций полей: φi – nsφd = φp, где φp – результирующий потенциал.
Так как на границе гидратного комплекса энергия определяется тепловой энергией движения молекул воды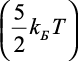 
, то получаем
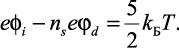(2.30)
То есть разность между энергиями иона и n молекулами растворителя компенсируется на границе сольватной системы тепловой энергией диэлектрической среды. Подставив (2.29) в (2.30), получим:
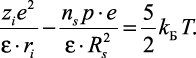(2.31)
Таким образом, решение последнего уравнения относительно ns приводит к уравнению
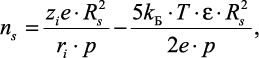(2.32)
где ri – радиус иона.
Оценка масс ms сольватированных ионов, входящих в последующем в уравнение для подвижности ионов, возможна по формуле:
ms = m + n·M, (2.33)
|
где m – |
масса несольватированного иона; |
|
M – |
молярная масса растворителя, дает основу для расчета приведенных масс сольватированных ионов |
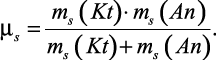(2.34)
Молекулы растворителя в сольватном комплексе поляризованы и сольватный комплекс (центральный ион и ns молекул растворителя) рассматривается как система связанных зарядов. Если начало координат совместить с центром иона, то возможно появление пространственной и частотной дисперсии молекул растворителя относительно их равновесных положений, ограниченных объемом самой оболочки. Другими словами, молекулы растворителя совершают финитное движение в ограниченном объеме пространства. Согласно [4], одномерное финитное движение является всегда колебательным – частицы совершают периодически повторяющееся движение в потенциальной яме с отмеченной выше частотной и пространственной дисперсией, отмеченной в уравнении Власова:
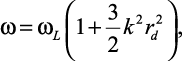(2.35)
|
где ωL – |
ленгмюровская плазменная частота; |
|
k – |
волновое число; |
|
rd – |
дебаевский радиус. |
Основной проблемой теории электролитов является определение энергии многочастичных взаимодействий в растворах электролитов как функции концентрации последних. Перспективы решения этой проблемы дает ленгмюровская частота незатухающих малых колебаний:
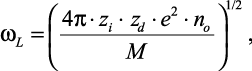(2.36)
|
где zie – |
заряд иона; |
|
zde – |
заряд диполя растворителя; |
|
|
плотность дипольных зарядов молекул растворителя в сольватном комплексе; |
|
rsi – |
радиус сольватированного иона. |
–
Дипольный заряд равен
,
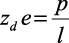где l – дипольное расстояние в молекуле растворителя.
Уравнение Власова учитывает частотную и пространственную дисперсию, и поэтому является наиболее общим дисперсионным уравнением для системы зарядов с любой геометрией. Параметр затухания krd имеет пределы изменения 0 ≤ krd ≤ 1. При krd = 0, пространственная дисперсия стремится к нулю и система может рассматриваться как однородная и изотропная. Этим требованиям обычно отвечают твердые тела с кубической решеткой.
В случае растворов электролитов krd = 1 пространственная дисперсия максимальна, тогда выражение (2.35) будет иметь вид:
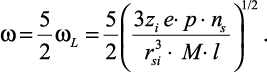(2.37)
Распределение вещества и заряда в данном случае сферически – симметричное. Умножив выражение (2.37) на постоянную Планка ћ и учитывая, что полная энергия ћω, согласно теореме вириала, равна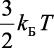 
(при сферически-симметричном распределении учитываются все три степени свободы), получим уравнение:
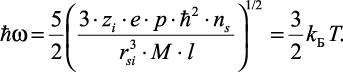(2.38)
Решение этого уравнения относительно rsi дает
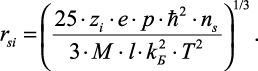(2.39)
Что касается l, то выбор его неоднозначен. В частности, для воды принято дипольное расстояние l = 1,38⋅10–8 см. В то же время в качестве l можно принять эффективный радиус мо-
лекулы воды Rs.
Таким образом, возможно нахождение ns по (2.32) для определения радиуса сольватированного иона по (2.39) и оценка μs по (2.34), использующихся в модельном уравнении для определения коэффициента теплопроводности.
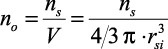