
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.3. Функции и графики функций
MathCAD допускает определение на листе новых функций от одного и более аргументов. Определение записывается в строчку в следующем порядке:
1.3.1. Имя новой функции. На имена функций распространяются те же правила, что и на имена переменных.
1.3.2. Список аргументов в круглых скобках через запятую.
1.3.3. Стандартный символ присваивания «: =».
1.3.4. Выражение, определяющее значение функции от аргументов.
Обращение к функции записывается в традиционной математической форме: упоминание имени функции, сразу после которого идет список значений аргументов в круглых скобках через запятую.
Пример:
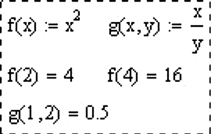
Построение графиков
Возможно построение следующих типов графиков:
1. Линейный (в прямоугольных и полярных координатах).
2. Линии уровня поверхности.
3. Поверхность.
4. Столбиковая диаграмма.
5. Точечный и векторный графики поверхности.
Для построения любого графика необходимо сначала определить на листе все данные, необходимые для построения, затем вставить
на лист соответствующий графический регион и связать его с отображаемыми данными. Для вставки графического региона можно использовать соответствующие кнопки панели Graph либо выбрать требуемый пункт в верхнем меню InsertGraph (или ВставкаГрафик). Связь с отображаемыми данными производится путем указания этих данных в позициях ввода графического региона.
Для регионов линейных графиков (рис. 15) заполняются две основные позиции ввода – слева и снизу от графика.
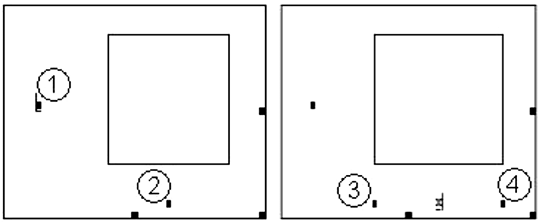
а б
Рис. 15. Вид региона для линейного графика до (а) и после (б) заполнения одной из основных позиций ввода
В нижней позиции 2 указывается выражение, определяющее значения абсцисс графика. Выражение – имя последовательности, вектора или обычной переменной. Может быть несколько выражений через запятую. При необходимости можно указать в дополнительных позициях 3 и 4 минимальное и максимальное значения.
В позиции 1 указывается выражение, определяющее значения ординат графика. Можно перечислить несколько выражений через запятую – в этом случае будет построено несколько графиков в одних координатах. Выражения обычно являются функциями от аргумента, указанного в позиции 2. Тем не менее, могут быть построены и графики от двух функций заданных параметрически, в этом случае в позициях 1 и 2 указываются имена этих функций (рис. 16).
Для регионов графиков поверхностей заполняется одна позиция ввода. Для графиков вида z = f(x, y) указывается либо имя
соответствующей функции от двух переменных, либо имя матрицы, содержащей значения z.
Для параметрических графиков (заданных функциями вида x = f1(u, v); y = f2(u, v); z = f3(u, v)) есть два способа построения. Рассмотрим наиболее универсальный способ. Построим график конусовидной поверхности, заданной параметрически:
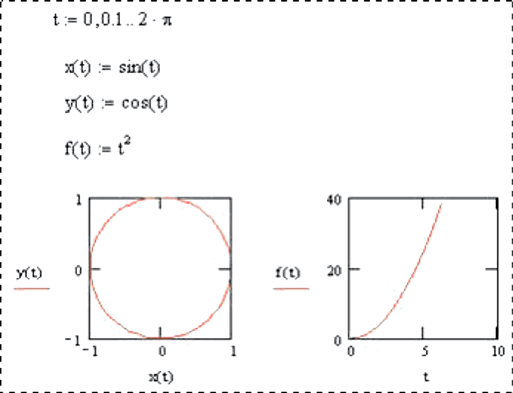
Рис. 16. Фрагмент листа MathCAD с линейными графиками двух функций (параметрической (x (t); y (t)) и обычной f (t))
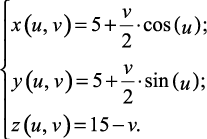
Пусть параметр u изменяется от 0 до 2π с шагом 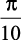 , а параметр v – от 0 до 15 с шагом 1. Необходимо определить законы вычисления трех матриц, каждая из которых будет содержать значения одной из координат точек поверхности. Число измерений каждой матрицы обычно равно числу параметров поверхности (в данном случае матрицы двумерные). Индексы последних элементов матрицы по каждому измерению определяются по формуле
, а параметр v – от 0 до 15 с шагом 1. Необходимо определить законы вычисления трех матриц, каждая из которых будет содержать значения одной из координат точек поверхности. Число измерений каждой матрицы обычно равно числу параметров поверхности (в данном случае матрицы двумерные). Индексы последних элементов матрицы по каждому измерению определяются по формуле
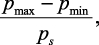
|
где pmax, pmin – |
максимальное и минимальное значения параметров соответственно; |
|
ps – |
шаг параметра. Индексы первых элементов матриц равны нулю. |
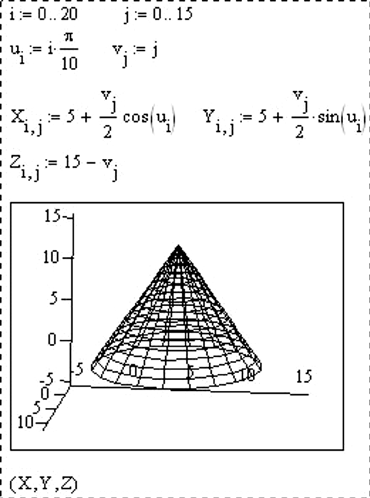
Рис. 17. Построение конусовидной поверхности в MathCAD
На листе MathCAD (рис. 17) сначала определяются последовательности, определяющие диапазоны изменения индексов матриц. Затем записываются законы вычисления векторов, содержащих
значения параметров. Данные законы имеют общий вид pk = pmin + k∙ps, где p – вектор параметров; k – индекс. Далее записываются законы вычисления матриц с координатами. Такими законами являются исходные параметрические выражения для координат, в которых вместо имен параметров подставляются элементы соответствующих векторов параметров. В последнюю очередь добавляется регион графика поверхности, где в позиции ввода в круглых скобках через запятую перечисляются имена трех матриц, содержащих значения координат x, y, z причем размерности матриц должны совпадать.
Второй способ построения параметрических поверхностей: на листе непосредственно записываются три параметрические функции, определяющие координаты, добавляется регион графика поверхности, после чего в позиции ввода региона в круглых скобках через запятую перечисляются имена указанных функций (без параметров).
Недостаток второго способа: MathCAD выберет диапазоны изменения параметров самостоятельно. Такой способ вполне пригоден для построения различных поверхностей вращения, все параметры которых находятся под функциями синуса или косинуса (например, тор или сфера).
Изменить различные параметры отображения графиков можно в специальном окне настроек, которое вызывается из раздела верхнего меню (FormatGraph или ФорматированиеГрафик).
