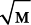Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.1. Модель и основные формулы
На основе разработанного метода расчета упругих, прочностных и теплофизических характеристик [2] появляется возможность конструирования материалов с учетом следующих принципов [3].
1. Цель конструирования материала. Постановка приоритетной задачи:
– достижение одного, двух параметров критериев оптимизации;
– компромиссный вариант по всем критериям (плотность, прочность, пластичность, вязкость, термостойкость, длительная жаропрочность, теплопроводность, тепловое расширение).
2. Обеспечение резервов доводки требуемых критериев материала.
В частности, кристаллографическое направление ⟨001⟩ монокристаллической лопатки может обеспечить резерв повышения модуля упругости за счет направлений ⟨110⟩, ⟨111⟩. А низкая плотность материала – повышение частоты вращения ротора.
3. Взаимозависимость и взаимовлияние характеристик материалов и независимость характеристик материалов.
В частности, изменение модуля упругости влияет на пластичность и термостойкость.
4. Использование в композиции материала только всесторонне и многократно исследованных компонентов.
5. Создание резервов по «критическим» элементам для достижения цели проекта.
В результате закладывается основа решения прямой задачи – создания материала с заданными характеристиками.
Расчетная модель
Модуль упругости E рассчитывается для элементарной атомной ячейки по теоретической формуле [4–7], основанной на электростатической природе упругости и выведенной из законов Кулона и Гука
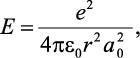 (1.1)
(1.1)
где e = 1,6∙10–19, Кл – величина взаимодействующих зарядов, равная элементарному заряду; p = 3,14; e0 = 8,85∙10–12 Кл2/Нм2 – электрическая постоянная; a0 – период кристаллической решетки; r – расстояние между взаимодействующими зарядами (зависящее от a0 и кристаллографического направления (рис. 1.1)).
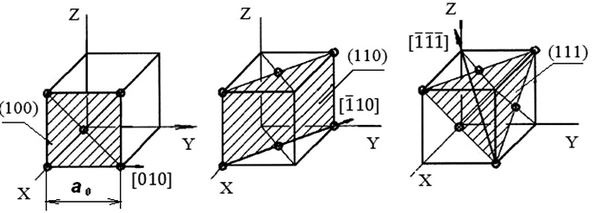
Рис. 1.1. Кристаллографические направления и плоскости ГЦК решетки
Коэффициент Пуассона рассчитывается по теоретической формуле [8, 9], основанной на электростатической природе упругости и выведенной из закона Кулона. Определяется величина поперечной деформации монокристалла в условиях кубической симметрии при заданной относительной продольной деформации ex = 0,1
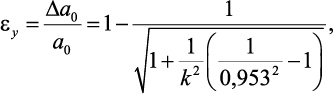 (1.2)
(1.2)
где k = 1 + kстрNорб, kстр – коэффициент, учитывающий тип структуры монокристалла; Nорб – среднее число незаполненных орбиталей внешней электронной оболочки атома; Dа0 – изменение периода кристаллической решетки.
Например, для железа Fe конфигурация внешних орбиталей 3d64s2, т.е. количество незаполненных орбиталей четыре, так как d10–d6 = d4.
Затем определяется коэффициент Пуассона монокристалла
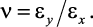
Тангенциальная составляющая предела упругости при сдвиге в элементарной атомной ячейке монокристалла рассчитывается по теоретической формуле [10, 11]
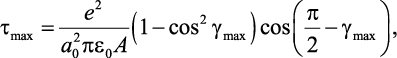 (1.3)
(1.3)
где gmax – максимальный угол сдвига, соответствующий пределу упругости; A – площадь сдвига.
Предел текучести при растяжении монокристалла рассчитывается по теоретической формуле [12, 13], основанной на механизме перемещения краевой дислокации и электростатической природе межатомного взаимодействия
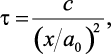 (1.4)
(1.4)
где с – коэффициент, определяемый в точке [tmax; x/a0]; x – величина перемещения в элементарной атомной ячейке при сдвиге.
Связь между нормальной и тангенциальной проекциями напряжения сдвига бездефектного монокристалла определяется по формуле [14]
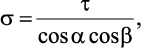
где a – угол между горизонтальной плоскостью и плоскостью сдвига; b – угол между плоскостью сдвига и направлением нормального напряжения.
В расчетах на прочность элементов турбины важную роль играют характеристики пластической деформации и ползучести. Рассматривается один из механизмов пластической деформации и установившейся ползучести, основанный на перемещении краевых дислокаций. В этом случае для определения величины пластической деформации и ползучести необходимо знать скорость перемещения дислокации.
Для решения поставленной задачи рассматривается движение одной краевой дислокации в нанообъеме бездефектного монокристалла. Схема сдвига с образованием краевой дислокации в нанообъеме монокристалла приведена на рис. 1.2.
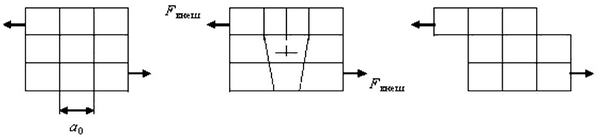
Рис. 1.2. Схема сдвига при пластической деформации и установившейся ползучести нанообъема монокристалла (Fвнеш – внешняя сила)
Начальная скорость перемещения краевой дислокации u0 рассчитывается по теоретической формуле [15, 16], основанной на электростатической природе межатомного взаимодействия
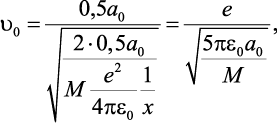 (1.5)
(1.5)
где 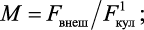
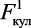 – кулоновская сила межатомного взаимодействия.
– кулоновская сила межатомного взаимодействия.
Поскольку в процессе движения дислокации происходит периодический разрыв межатомной связи, то скорость движения дислокации изменяется от нулевого значения до u0. Средняя скорость движения дислокации определяется как 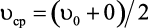 .
.
Зная скорость перемещения дислокации в нанообъеме, можно перейти к расчету величины пластической деформации в нитевидном (бездефектном) монокристалле, который используется в качестве армирующей фазы в эвтектическом композитном материале.
Для определения скорости деформации ползучести технических монокристаллов, имеющих плотность дислокаций до 103 см–2, используется формула Орована
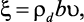 (1.6)
(1.6)
где x – скорость деформации ползучести; ρd – плотность дислокаций; b – вектор Бюргерса; u – скорость движения дислокации [17].
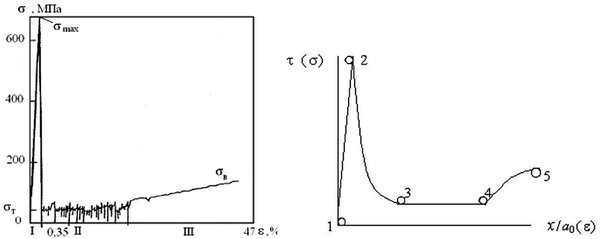
На основе предложенных теоретических методов расчета разработана математическая модель диаграммы «напряжение – деформация» для монокристаллов. Используя численные значения опорных точек 1-2-3-4-5 (рис. 1.3, б), моделируется диаграмма «напряжение – деформация» для нанообъема монокристалла. Типичный характер диаграммы для монокристаллов металлов представлен на примере меди (рис. 1.3, а).
Данные, полученные по модели диаграммы монокристаллов тугоплавких металлов, интерметаллидов, карбидов, нитридов (рис. 1.3, б), являются исходными для расчета напряженно-деформированного состояния микрообъема эвтектического композита, а затем и для макрообъема – рабочей лопатки турбины ГТД.
а б
Рис. 1.3. Диаграмма растяжения нитевидного монокристалла:
а – экспериментальная, для меди [18]; б – математическая модель
Для расчета напряженно-деформированного состояния элементов турбины из эвтектических композитов и монокристаллических жаропрочных сплавов необходимо знать их теплофизические характеристики и плотность. В частности, коэффициент теплопроводности монокристаллов рассчитывается по теоретической формуле [19, 20], выведенной в соответствии с законом Фурье
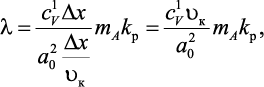 (1.7)
(1.7)
где 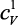 – теплоемкость одного атома при постоянном объеме; Dx – расстояние между ближайшими соседями атомами; mA – атомная масса химического элемента; kр – коэффициент ретикулярной плотности элементарной ячейки кристаллической структуры; uк – скорость распространения колебаний в монокристалле.
– теплоемкость одного атома при постоянном объеме; Dx – расстояние между ближайшими соседями атомами; mA – атомная масса химического элемента; kр – коэффициент ретикулярной плотности элементарной ячейки кристаллической структуры; uк – скорость распространения колебаний в монокристалле.
Такая теплофизическая характеристика, как коэффициент теплового расширения определяется теоретически в следующей последовательности. Вначале рассчитывается изменение периода кристаллической решетки вследствие повышения температуры, расчет которого основан на изменении энергии связи двух разноименных зарядов в кристаллической решетке.
Зависимость изменения периода кристаллической решетки от температуры рассчитывается по теоретической формуле [21]
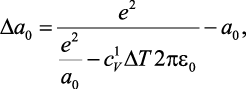 (1.8)
(1.8)
где Dа0 – изменение периода кристаллической решетки вследствие теплового воздействия; DТ – изменение температуры; 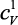 – теплоемкость атома при постоянном объеме.
– теплоемкость атома при постоянном объеме.
Для элементарной атомной ячейки кристаллической решетки коэффициент теплового расширения определяется как [22]
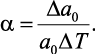 (1.9)
(1.9)
Получив расчетным путем исходные данные: значения модуля упругости и коэффициента теплового расширения, определяются термические напряжения σтерм по известным формулам, в частности,
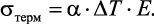 (1.10)
(1.10)
Плотность монокристаллов простых веществ рассчитывается по теоретической формуле [23]
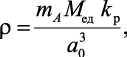 (1.11)
(1.11)
где Mед = 1,66⋅10–27 кг – атомная единица массы.
Плотность сложных веществ или соединений, состоящих из атомов разных химических элементов типа NbC, определяется как сумма плотностей составляющих химических элементов.
Результаты расчетов плотности некоторых металлов и соединений приведены в табл. 1.1.
Таблица 1.1
|
Наименование |
Величина плотности, кг/м3 |
Расхождение, % |
|
|
расчетная |
экспериментальная |
||
|
Mo (ОЦК) |
10219,9 |
10218 (10200) |
0,02 |
|
W (ОЦК) |
19248,5 |
19263 (19230) |
0,08 |
|
Ta (ОЦК) |
16678,6 |
16623 (16600) |
3,3 |
|
Nb (ОЦК) |
8581,5 |
8630 (8570) |
5,6 |
|
TaС (кубич) |
14625 |
14500 |
8,6 |
Примечание. В таблице приведены рентгеновская и пикнометрическая (в скобках) экспериментальные значения плотности [24].
В результате сравнительного анализа теоретического расчета упругих, прочностных, теплофизических и физических характеристик бездефектных монокристаллов установлена удовлетворительная сходимость с экспериментальными данными других авторов. Это позволило использовать полученные данные в качестве исходных для оценки прочностных характеристик композитов.
В условиях отсутствия экспериментальных данных разработанная модель позволяет моделировать кристаллическую структуру (на основе правил кристаллографии) и ее упругие характеристики бездефектных монокристаллов в составе эвтектического композита для лопаток газовых турбин.
Для моделирования элементарной ячейки кристаллической структуры соединения исходными данными являются химическая формула соединения, символ Пирсона и пространственная группа.
Из формул (1.1)–(1.4), в частности, можно сделать заключение, что управляющими факторами, определяющими свойства материала, являются следующие.
1. Металлургические факторы: химический состав (химическая формула); тип кристаллической решетки (ОЦК, ГЦК и др.); период кристаллической решетки а0.
2. Технологические факторы: кристаллографическое направление монокристалла; объемная доля армирующей фазы.
Управляющие факторы используются для конструирования материалов в соответствии со следующими основными принципами.
Принцип независимости характеристик материалов реализуется, в частности, на примере независимости упругих характеристик от химического состава жаропрочных никелевых сплавов.
Модуль упругости монокристаллических жаропрочных никелевых сплавов определяется матрицей монокристалла, т.е. g – твердым раствором, основой которого является кристаллическая решетка никеля (табл. 1.2).
Таблица 1.2
|
Наименование сплава или элемента и направление действия нагрузки |
Величина модуля упругости, ГПа |
Расхождение, % |
|
|
расчетная |
экспериментальная |
||
|
Ni (ГЦК) <100> <110> <111> |
140,2 210,3 262,9 |
138,0 215,0 [24] 262,0 |
1,6 2,1 0,3 |
|
ЖС ٦Ф моно <100> <110> <111> |
140,2 210,3 262,9 |
139[25] 220 305 |
0,9 4,5 13,8 |
|
ЖС ٣٢ <100> <110> <111> |
140,2 210,3 262,9 |
135…140 [26] – 280…300 |
3,8…0 – 6,0…12,3 |
|
ЖС ٣٦ моно <100> <110> <111> |
140,2 210,3 262,9 |
130[25] 215 305 |
7,8 2,3 13,8 |
Экспериментальные значения для ЖС 36 моно и ЖС 6Ф моно взяты из гра-
фика в [24].
Установлено, что расчетные значения модуля упругости монокристаллических жаропрочных никелевых сплавов в кристаллографическом направлении <100> имеют удовлетворительную сходимость с экспериментом с расхождением от 0,9 до 7,8 % (табл. 1.2). Полученные результаты позволяют обоснованно использовать модельную композицию Ni – NbC для оценки прочности лопатки из материала типа ВКЛС с кристаллографическим направлением <100> в области упругих деформаций.
Необходимо отметить также, что для кристаллографических направлений <110>, <111> максимальное расхождение расчета для рассматриваемых материалов (табл. 1.2) составляет 13,8 % (в частности, для сплава ЖС 36 моно).
Принцип взаимозависимости и взаимовлияния характеристик материалов реализуется, в частности, на примере влияния модуля упругости на другие упругие характеристики. Повышение модуля упругости ведет к соответствующему повышению предела упругости монокристалла и снижению коэффициента Пуассона. Введение в кристаллическую решетку никеля (твердого раствора) легирующего элемента Al, позволяет при практическом сохранении модуля упругости никеля уменьшить массу за счет уменьшения плотности. Тем самым улучшаются удельные характерис-
тики материала.
Последовательность решения задачи представлена в виде блок-схемы и этапов расчета прочности (рис. 1.4).
Первый этап – расчет упругих, прочностных, теплофизических и физических характеристик нанообъема нитевидного монокристалла – элементарной атомной ячейки. Для новых и перспективных материалов этот этап предусматривает моделирование его кристаллической структуры на основе химической формулы, индекса Пирсона и пространственной группы.
Второй этап – расчет упругих, прочностных, теплофизических и физических характеристик представительного микрообъема эвтектического композитного материала или монокристаллического жаропрочного сплава на основе результатов расчета первого этапа.
Третий этап – расчет методом конечных элементов напряженно-деформированного состояния макрообъема эвтектического композитного материала или монокристаллического жаропрочного сплава – бездефектной рабочей лопатки турбины.
Напряженно-деформированное состояние лопатки из эвтектического композита рассчитывается с учетом следующих допущений: свойства границ фаз не учитываются, так как армирующая фаза формируется в процессе кристаллизации и представляет собой единое целое с матрицей; эвтектический композит рассматривается как ортотропный материал с бездефектной структурой армирующей фазы; объем лопатки моделируется как однородное ортотропное тело с симметрией относительно срединной поверхности.
Переход в расчетах от нанообъема к микрообъему и макрообъему основан на бездефектной структуре нитевидного монокристалла. Нанообъем – элементарная атомная ячейка – периодически повторяется в нитевидном монокристалле. В поперечном направлении нанообъем, периодически повторяясь, достигает микрообъема. В продольном направлении микрообъем, периодически повторяясь, достигает макрообъема, т.е. длина волокон равна длине пера лопатки.
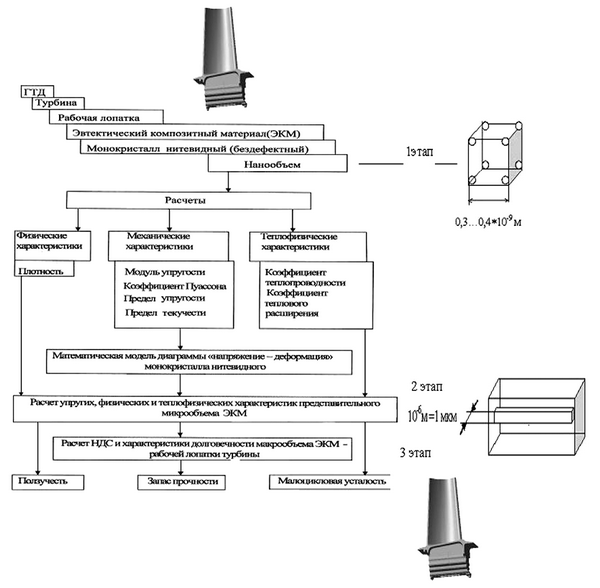
Рис. 1.4. Этапы расчета
Разработанный метод расчета позволяет установить влияние параметров кристаллической решетки материала, силы химической связи на упругие и прочностные характеристики. Иначе говоря, оценено влияние химического состава материала (металлургический фактор) на конструкционную прочность лопатки. Кроме того, разработанный метод заложил основу конструирования лопаток с заданными механическими и теплофизическими характеристиками.
Приложение результатов
Для определения напряженно-деформированного состояния и расчета на прочность лопаток методом конечных элементов необходимо иметь комплекс исходных данных: модуль упругости с учетом анизотропии; коэффициент Пуассона; предел текучести с учетом анизотропии; коэффициент теплопроводности; коэффициент теплового расширения; модуль упругости и коэффициент теплового расширения в зависимости от температуры; плотность материала. Необходимо отметить, что методика расчета получила дальнейшее развитие в работах [26–29]. Разработанный метод позволяет дополнять ограниченный объем экспериментальных данных по этим характеристикам результатами теоретического расчета.
В частности, для модуля упругости получены температурные зависимости для монокристаллов металлов, карбидов, нитридов, интерметаллидов, входящих в состав жаропрочных сплавов лопаток турбин, а также для углеродных нанотрубок – компонентов нанокомпозитов (рис. 1.5–1.8).
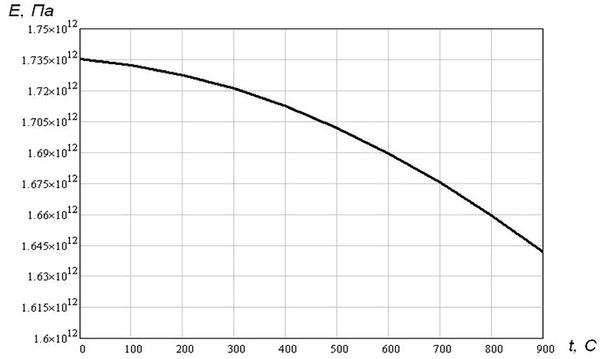
Рис. 1.5. Теоретическая зависимость модуля упругости углеродной нанотрубки от температуры в направлении вектора r1 [5]
Например, для монокристалла интерметаллида Ni3Al известны экспериментальные данные [30] в кристаллографическом направлении <111>. Результаты расчета имеют удовлетворительную сходимость (рис. 1.6).
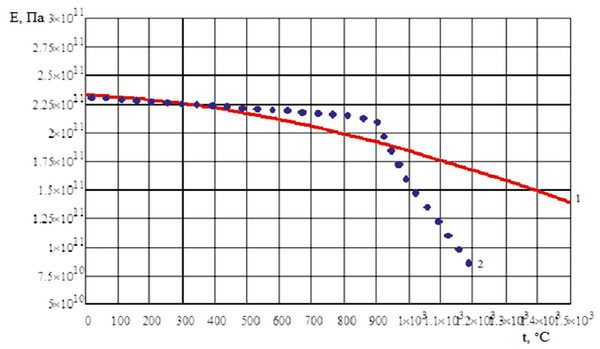
Рис. 1.6. Температурная зависимость модуля упругости интерметаллида
Ni3Al в направлении <111>:
1 – расчетные значения; 2 – экспериментальные значения [30]
С учетом этих данных рассчитаны зависимости для направлений <100>, <110> и для поликристаллического состояния (рис. 1.7), что существенно дополняет недостающую экспериментальную информацию.
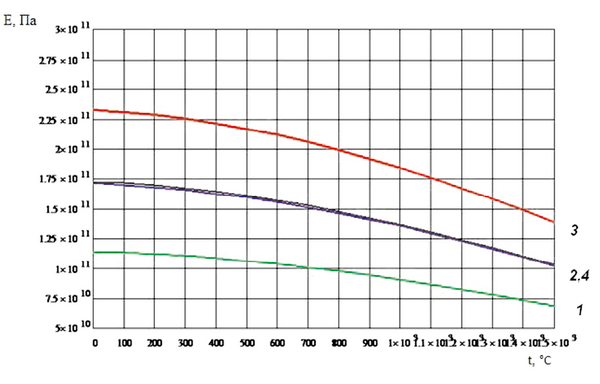
Рис. 1.7. Температурная зависимость модуля упругости монокристалла интерметаллида Ni3Al:
1 – модуль упругости в направлении <100>; 2 – модуль упругости в направлении <110>;
3 – модуль упругости в направлении <111>; 4 – модуль упругости поликристалла
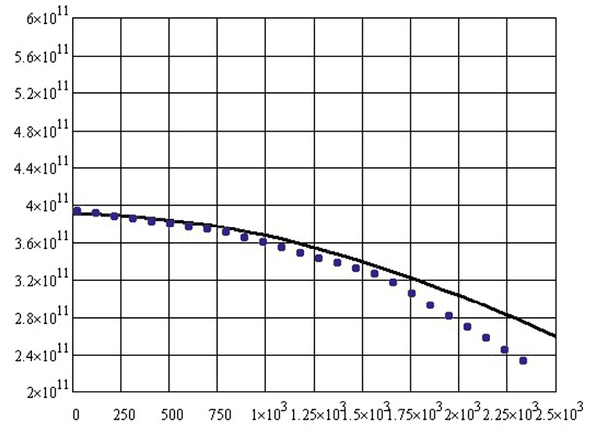
Рис. 1.8. Теоретическая зависимость модуля упругости поликристаллического
от температуры: …. – экспериментальные значения [24]
Разработанная модель позволяет на основе ограниченных экспериментальных данных строить диаграммы ползучести. На рис. 1.9 приведена диаграмма для эвтектического композита ВКЛС-10.
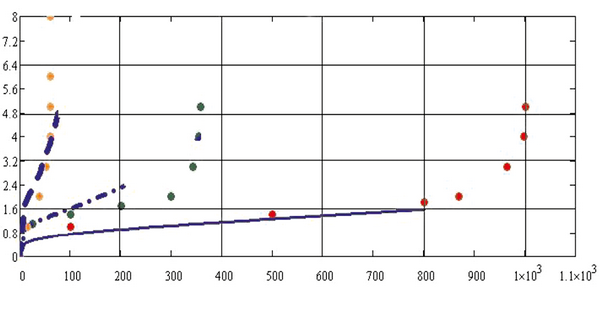
Рис. 1.9. Модель диаграммы ползучести сплава ВКЛС-10:
…. – экспериментальные значения [31]
Учет сил межатомного взаимодействия позволяет теоретически определить величины коэффициента интенсивности напряжения (при плоском нагружении) и ударной вязкости. Первые оценочные результаты этих величин для некоторых элементов и соединений приведены в табл. 1.3, 1.4.
Таблица 1.3
|
Наименование элемента |
Величина коэффициента интенсивности |
Источник |
|
|
расчетная |
экспериментальная |
||
|
Cu Cплавы Cu |
48,3 – |
– 50…110 |
– [32] |
|
Al Cплавы Al |
30,5 – |
– 10…60 |
– [32] |
|
Fe Стали |
117,1 – |
– 20…150 |
– [32] |
|
Ni Cплавы Ni |
76,0 – |
– 60…110 |
– [32] |
|
W |
7,4 |
4…7,5 |
[33] |
|
Mo |
6,5 |
– |
– |
|
Cr |
5,8 |
– |
– |
|
Ni3Al Cплавы Ni |
79,2 – |
– 60…110 |
– [32] |
Таблица 1.4
|
Наименование элемента |
Величина ударной вязкости, МДж/м2 |
Источник |
|
|
расчетная |
экспериментальная |
||
|
Cu |
1,96 |
1,76 |
[24] |
|
Al |
1,24 |
0,71…3,35 |
[24] |
|
Fe |
2,82 |
2,35 |
[24] |
|
Ni |
3,15 |
3,34…3,68 |
[24] |
|
W |
0,165 |
0,245…0,294 |
[24] |
|
Cr |
0,14 |
0,02 |
[24] |
|
Ni3Al |
2,96 |
– |
– |
Кроме того, зная температурные зависимости модуля упругости, коэффициента теплового расширения и коэффициента Пуассона, можно оценить величину термических напряжений на границе волокно-матрица эвтектического композита.
Полученный комплекс расчетных характеристик материала позволяет сформировать исходные данные для оценки напряженно-деформированного состояния и запаса прочности лопатки турбины из проектируемого материала.
Исходя из вышеизложенного, можно сделать следующие выводы:
1. Заложена основа методики конструирования материалов, которая позволяет, складывая атомы как «кирпичики», «строить здание» нового материала с заранее известными свойствами.
2. Заложена основа методики моделирования кристаллической структуры и упругих свойств монокристалла в условиях ограниченного объема экспериментальных данных.
3. Разработанный метод позволяет исследовать влияния металлургических, технологических и эксплуатационных факторов на конструкционную прочность лопатки из эвтектических композитов различного состава при различных режимах работы двигателя, в частности, оценивать изменение запасов прочности лопатки в зависимости:
– от объемной доли армирующей фазы (волокна);
– направления кристаллизации эвтектического композита <100>, <011>, <111>, которое влияет на его упругие и теплофизические характеристики;
– остаточных термических напряжений на границе волокно–матрица.
4. Возможна теоретическая оценка удельных характеристик композитов, таких, например, как Е/r.