Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОТ ЧЕТЫРЕХ К ОДНОМУ. СИЛЫ ВНУТРИАТОМНОГО ВЗАИМОДЕЙСТВИЯ И ПРОЧНОСТЬ МАТЕРИАЛОВ

Бадамшин И Х,

1.2. Зависимость периода кристаллической решетки от температуры

Перспективными материалами для рабочих лопаток газовых турбин являются эвтектические композиты [34], в состав которых входят нитевидные монокристаллы и дисперсно-упрочненная монокристаллическая матрица.

Помимо обычных факторов, определяющих свойства композиций, таких как природа и соотношение компонентов, распределение их и др., термическое расширение композиционного материала в значительной степени определяется наличием в нем остаточных напряжений. В композиционном материале возникают напряжения, обусловленные различием коэффициентов теплового расширения компонентов. При некоторой температуре эти напряжения достигают предела текучести матрицы [35].

Для оценки коэффициента теплового расширения композита aкм в целом необходимо знать его составляющие: вдоль (α1) и поперек (α2) волокон в зависимости от коэффициентов теплового расширения волокон и матрицы αв, aм. Для изотропных волокон и матрицы такие соотношения приведены в работах [36, 37]. Для монокристаллов анизотропия a может достигать 300 % и более [38].

Задача определения αв, aм для монокристаллов решается, например, с учетом межатомного взаимодействия в кристаллической решетке. Так, коэффициент теплового расширения связан с температурой плавления и может характеризовать силу межатомной связи [38].

Максимальная сила межатомной связи приходится на металлы с максимальными температурами плавления и минимальными значениями коэффициента термического расширения. Соответственно, эти металлы имеют и минимальные межатомные расстояния.

Для металлов с кубической решеткой коэффициент a связан с температурой плавления соотношением 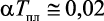. Кроме того, для веществ с металлическим характером связи имеется эмпирическое соотношение 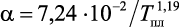[38]. Однако эти соотношения не позволяют установить зависимость коэффициента теплового расширения от эксплуатационной температуры.

Расчет a, учитывающий ангармоническую составляющую колебаний атомов, по формуле [39]

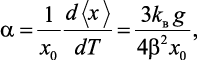
где g и b – функции потенциала U; x – расстояние; Т – температура, предполагает знание потенциала кристаллической решетки U и также не имеет методики инженерного расчета коэффициента теплового расширения.

Для оценки коэффициента теплового расширения по формуле Гилмана [38] необходимо знать силу межатомного сцепления

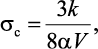
где k – постоянная Больцмана; V – средний атомный объем.

Поэтому актуальной является задача вывода аналитической формулы и разработки инженерной методики расчета коэффициента теплового расширения применительно к монокристаллам материалов лопаток газовых турбин.

Модель и сравнение с экспериментом

Армирующей фазой в эвтектических композитах является нитевидный монокристалл. В нем рассматривается элементарная атомная ячейка. Кристаллическая решетка, находится в равновесном состоянии (силы притяжения уравновешены силами отталкивания). Потенциальная энергия взаимодействия зарядов U0 – величина постоянная, то есть решается статическая задача.

Расчет изменения периода кристаллической решетки вследствие повышения температуры основан на учете изменения энергии связи двух разноименных зарядов в атомной ячейке кристаллической решетки, т.е. между узлом решетки и электронным облаком в межузловом пространстве.

Энергия электростатической связи двух разноименных зарядов атома в кристаллической решетке в соответствии с законом Кулона определяется по формуле

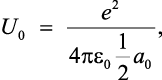
где а0/2 – расстояние между разноименными зарядами (узлом кристаллической решетки и электронным облаком).

Тепловая энергия атома при нагреве ячейки монокристалла на величину DТ определяется как

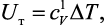
где 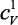– теплоемкость атома при постоянном объеме. В соответствии с законом Дюлонга и Пти

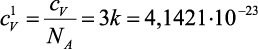Дж/К,

где NA – число Авогадро.

Энергия связи двух разноименных зарядов атома в ячейке кристаллической решетки вследствие нагрева уменьшается на величину

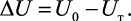
Изменение среднего расстояния между зарядами вследствие нагрева кристаллической решетки

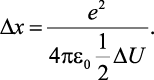
Изменение периода кристаллической решетки вследствие нагрева

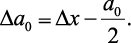
После преобразований зависимость изменения периода кристаллической решетки от температуры примет следующий вид [22]:

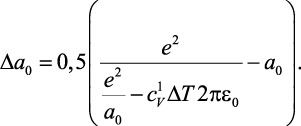(1.12)

Вследствие периодичности и симметрии бездефектного монокристалла свойства элементарной атомной ячейки передаются кристаллической решетке. Поэтому для атомной ячейки и кристаллической решетки в целом коэффициент теплового расширения определяется как

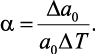(1.13)

Результаты расчета а0 в зависимости от температуры для некоторых металлов приведены в табл. 1.5.

Таблица 1.5

Примечание. Величина периода кристаллической решётки а0 приведена в ангстремах. Экспериментальные значения а0эксп взяты
из работы [38].

Графическая зависимость периода кристаллической решетки от температуры, в частности, для хрома, приведена на рис. 1.10.

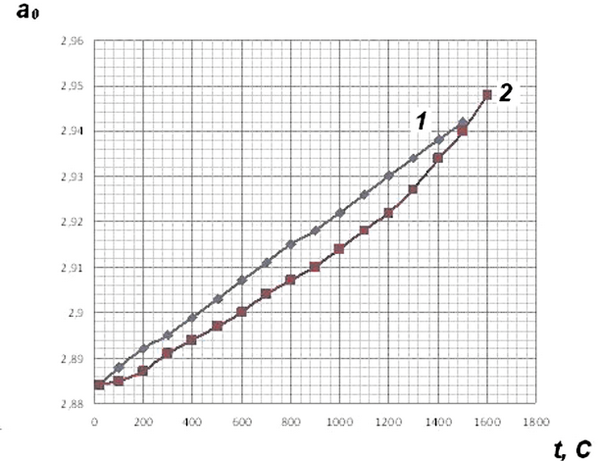
Рис. 1.10. Графическая зависимость периода кристаллической решетки
(в ангстремах) от температуры для хрома:
1 – эксперимент [38]; 2 – расчет

Из табл. 1.5 и рис. 1.10 видно, что результаты расчета а0 в зависимости от температуры удовлетворительно сходятся (с расхождением до 3,3 %) с экспериментальными данными работы [38]. На рис. 1.11 приведены экспериментальные зависимости [38].

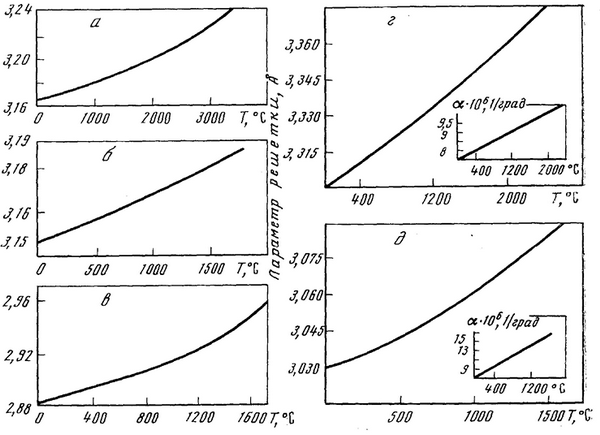
Рис. 1.11. Экспериментальные зависимости [38]:
а – W; б – Mo; в – Cr; г – Nb; д –V

Результаты расчета периода кристаллической решетки в зависимости от температуры а0 в дальнейшем используются для определения:

– коэффициента теплового расширения [22];

– модуля упругости [5];

– предела упругости и др. характеристик [40].

В частности, в работе [5] приведены результаты расчета модуля упругости углеродной нанотрубки (УНТ). Уточненные значения для УНТ приведены в табл. 1.6.

Таблица 1.6

Расчетные значения модуля упругости УНТ в зависимости от температуры

Полученные формулы (1.12)–(1.13) позволяют определять теоретическую зависимость периода кристаллической решетки от температуры и значительно сократить объем дорогостоящих экспериментов.

Результаты расчета коэффициента теплового расширения армирующей фазы и матрицы эвтектического композита являются исходными данными для оценки термических напряжений в материале лопатки турбины.