
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.2. Методы математического моделирования и оптимизации при управлении технологическими объектами в условиях многокритериальности
1.2. Методы математического моделирования и оптимизации при управлении технологическими объектами в условиях многокритериальности
В настоящее время с развитием науки, техники и производства технологические объекты нефтепереработки, как и другие производственные объекты, непрерывно усложняются, и уже сейчас говорят об этих объектах как о некоторой сложной системе, которая состоит из различных компонентов, взаимосвязанных друг с другом и характеризующаяся множеством критериев экономического, экологического характера [36]. Поэтому методы многокритериального принятия оптимального решения по управлению на базе системного моделирования, предлагаемые в данной монографии, являются наиболее эффективными и перспективными методами исследования и решения производственных задач нефтепереработки.
При применении методов системного математического моделирования технологических систем нефтепереработки необходимо, прежде всего, четко определить цель моделирования. Поскольку невозможно полностью смоделировать реально функционирующую систему – исследуемую технологическую установку нефтепереработки (систему-оригинал), создается математическая модель (система-модель) под поставленную проблему. Таким образом, применительно к вопросам моделирования цель возникает из требуемых задач моделирования, что позволяет подойти к выбору критерия и оценить, какие элементы войдут в создаваемую модель.
Совокупность элементов и связей между ними позволяет судить о структуре системы. При математическом описании производственной системы рассматриваются отдельные функции, т.е. алгоритмы поведения системы. Такое описание структуры реализуется при применении функционального подхода, оценивающего функции, которые выполняет система, причем под функцией понимается свойство, приводящее к достижению цели. При наличии некоторого эталона сравнения можно ввести количественные и качественные характеристики систем. Для
количественной характеристики вводятся числа, выражающие отношения между данной характеристикой и эталоном. Качественные характеристики системы находятся, например, с помощью методов экспертных оценок [37–39] и теории нечетких множеств [40–42]. В производственных условиях часто эксперты затрудняются оценивать ситуации, зависимость, влияния параметров количественно, даже с помощью шкал. В таких случаях приходиться проводить экспертную оценку в нечеткой среде, т.е. качественную экспертизу, но в научной литературе это направление слабо исследовано и нет методов организации и проведения такой экспертной процедуры. Предложенный автором метод решения данной проблемы [43] описан в следующем разделе.
Модель – это материальный объект или идеальная (в смысле отражения реальной действительности) копия исходного объекта, находящаяся в таком сходстве с ним, что отражает его существенные стороны и обеспечивает более полное познание. Бывают разные типы моделей, нами рассматриваются математические модели, в которых моделирование объектов и процессов осуществляют с применением математического описания исследуемого объекта или процесса.
В данной работе объектами исследования являются технологические агрегаты нефтеперерабатывающего производства, которые предназначены для систематического производства нефтепродуктов, определенного качества и в заданном количестве. Для реализации результатов исследования выбран конкретный объект нефтепереработки – блок каталитического риформинга установки ЛГ-35-11/300-95 Атырауского НПЗ. По результатам исследования и по разработанным математическим моделям объекта исследования решаются проблемы принятия оптимального режима работы блока риформинга по экономико-экологическим и другим критериям. В качестве методов решения поставленной задачи выбраны методы математического моделирования и принятия решений с учетом нечеткости части исходной информации, позволяющие эффективно управлять технологическими объектами и процессами нефтепереработки в производственных условиях. В ходе постановки и решения задачи будут формализованы новые постановки задачи исследования, а также разработаны новые методы и алгоритмы моделирования и принятия решений в нечеткой среде.
Исследования на моделях и поэтапное моделирование необходимо практически осуществлять для сокращения сроков создания и промышленного освоения новых процессов, различного типа оборудования и управления их работой, для оптимизации производственных процессов. С помощью математических методов на различных стадиях исследования могут решаться такие задачи, как выбор решения по определению типа процесса для переработки нефти, выбор типа технологических агрегатов и устройств, их оптимальное размещение, оптимальное решение производственной задачи с подбором оптимальных условий работы каждого аппарата блока и всего комплекса в целом.
В последнее время развитие нефтеперерабатывающего производства осуществляется в основном путем углубления переработки, разделения, очистки и других процессов, что приводит к усложнению агрегатов и технологии. Эта сложность появляется в многообразии параметров, характеризующих протекание процессов, в большом числе внутренних связей между параметрами и их взаимном влиянии. Для ведения технологического процесса в желаемом режиме в комплексе технологических агрегатов необходимо установить закон взаимосвязи между входными и выходными параметрами отдельных агрегатов, что невозможно осуществить без специальных средств и математического аппарата. Эффективное решение этой задачи и управление сложными промышленными установками возможно с помощью компьютерных систем на основе математических моделей и алгоритмов принятия оптимального решения, созданных с учетом природы и строения промышленной установки или комплекса установок, типа процессов, протекающих в них, видов режимов.
Математическая модель представляет собой систему математических описаний, отражающих особенности процессов, протекающих в объекте моделирования (технологическом агрегате), которая с помощью определенного алгоритма позволяет прогнозировать поведение объекта при изменении входных и управляющих параметров. Формально математическое описание представляет собой совокупность зависимостей, связывающих различные параметры объекта, процесса в единую систему соотношений [36, 44, 45]. Среди этих соотношений могут быть выражения, отражающие общие физические законы (например, законы сохранения массы и энергии), уравнения, описывающие «элементарные» процессы (например, взаимодействия, химико-физические превращения). Кроме того, в состав математического описания входят также различные эмпирические и полуэмпирические зависимости между разными параметрами объекта, теоретическая форма которых неизвестна или слишком сложна.
Рассмотрим основные функции математических моделей, используемые при решении задач анализа и управлении сложными технологическими объектами. Моделирование может использоваться для разработки теории объекта, особенно если непосредственное исследование объекта или процесса невозможно, т.е. анализ моделей зачастую позволяет обеспечить развитие теории. Так, например, современный уровень знаний не позволяет создать строгую теорию парообразования и на основании ее получить аналитические выражения для определения коэффициентов теплоотдачи при кипении [46, 47]. Моделирование дает возможность в отдельных случаях заменить вычисления измерениями или упростить задачу.
Математическое моделирование становится особенно целесообразным, когда разрабатываются или исследуются дорогостоящие объекты, например крупные технологические установки для исследования таких объектов, при определении рациональных режимов их эксплуатации. Применение математических моделей сложных промышленных объектов может приносить значительный экономический эффект. Оно позволяет проводить исследования процессов, происходящих в технологических агрегатах, при неизмеримо меньших затратах, чем натурные исследования на реальных агрегатах, на стендах или на физических моделях. Наконец, пакет математических моделей (модели агрегатов, объединенные в общую систему) может использоваться для эффективного решения задач принятия решений, оптимизационных задач и для выработки управляющих воздействий по оптимальному ведению технологического процесса и его интенсификации.
Таким образом, методы математического моделирования позволяют объективно рассмотреть и сопоставить множество различных вариантов по локальным критериям и выбрать наиболее целесообразный, т.е. являются средством решения прямых задач управления различными объектами (моделирование), когда определяются влияния входных управляющих параметров объекта на выходные. Решения таких задач применительно к различным объектам нефтеперерабатывающей, химической и др. промышленностей рассмотрены в работах [48–63].
Кроме того, на основе моделей, позволяющих определить зависимость критериев качества от управляющих параметров, можно решать обратные задачи. При этом задаются требования к выходным параметрам объекта, например, желаемые значения выхода и качества получаемых продуктов, и ограничения по ведению процесса, обусловленные технологическим регламентом установки (интервалы значений режимных параметров, управляющих воздействий и др.). Затем, применяя специальные алгоритмы принятия оптимального решения, определяют набор управляющих параметров, обеспечивающих эффективные значения критериев качества. Анализируя полученные результаты оптимизации, осуществляется выбор альтернатив, т.е. решения обратных задач – задач принятия решений [64–68]. Методы принятия в условиях нечеткости исходной информации описаны например в следующей литературе [69–71], а теория оптимизации по многим критериям описана в [72–75]. Проблемы и подходы к решению рассмотренных выше прямых и обратных задач, возникающих при управлении сложными технологическими объектами нефтепереработки по экономико-экологическим критериям, являются целью исследования данной монографии.
Как уже отмечено, технологические установки нефтеперерабатывающей промышленности состоят из нескольких взаимосвязанных технологических агрегатов. Поэтому для ведения технологического процесса в оптимальном режиме необходимо иметь связанные математические модели агрегатов установки, составленные на основе системного подхода. Эти модели должны позволять прогнозировать влияния параметров агрегатов на протекающие в них процессы, на промежуточные и конечные продукты и на работу установки в целом. Для математического описания связей интересующих нас параметров исследуемого объекта обычно используется комбинированная информация разных типов:
● теоретические представления о природе и характере процесса, протекающего в объекте [54, 55, 58];
● исходные статистические данные, характеризующие функционирование анализируемой системы [76, 77];
● данные экспертной оценки, в том числе нечеткая информация, качественно описывающие состояния объекта [78–81].
В зависимости от доступности тех или иных видов перечисленных данных могут быть построены различные типы моделей агрегатов установки. При этом следует отметить, что при создании комплекса моделей для системного моделирования блока, установки необходимо учитывать, хорошо ли стыкуются разработанные типы моделей отдельных агрегатов.
По своему назначению, по выполняемым функциям и по точности можно условно выделить следующие разновидности моделей [36]:
● информационные модели, используемые в качестве советующих систем для изучения влияния факторов на выходные параметры для разработки рекомендаций по корректировке режима работы установки и т.д.;
● оптимизационные модели, используемые для поиска оптимальных условий протекания процесса в комплексе агрегатов. В качестве оптимизационных могут использоваться информационные модели, дополненные блоком оценки результата на основе целевой функции с учетом налагаемых ограничений на изменение входных и выходных переменных, а также блоком оптимизации для поиска такого сочетания входных – управляющих переменных, при котором выходные переменные достигают желаемых значений;
● модели управления процессом, используемые для воздействия на систему в реальном масштабе времени с целью компенсации
нежелательных случайных возмущений и смещения системы в направлении экстремального значения целевой функции. Такая модель является компонентом системы автоматического управления (регулирования), включающей датчики состояния системы, преобразователи сигналов датчиков, а также исполнительные механизмы для реализации требуемого воздействия. К этим моделям предъявляются повышенные требования по точности.
Основными подходами к построению математических моделей агрегатов являются: теоретический, экспериментально-статистический, подход, основанный на использовании методов теории нечетких множеств, и комбинированный подход [82].
Рассмотрим основные типы математических моделей, получаемых на основе перечисленных подходов и используемых при исследовании и управлении технологическими агрегатами промышленных установок.
Детерминированные модели технологических агрегатов и процессов разрабатываются на основе теоретических представлений о структуре описываемой системы и закономерностях функционирования ее отдельных подсистем, т.е. эти модели строятся на основе теоретического подхода, использующего уравнения, описывающие каждый из существенных для данного натурного объекта процессов, например, имеются примеры детерминированных моделей наиболее изученных физико-химических процессов нефтепереработки и нефтехимии (движение жидкости и газа, тепло- и массоперенос, кинетика химической реакции, процессы в потоке – идеальное смещение, вытеснение, диффузия и т.д.) [48, 58].
Построение моделей технологических агрегатов путем теоретического подхода возможно в основном для простейших процессов. Для более сложных агрегатов, или когда имеется комплекс взаимосвязанных агрегатов, получение их детерминированных моделей практически невозможно. Это связано с тем, что в этих случаях отсутствуют или ограничены теоретические сведения о характере процессов моделируемого объекта, или получаемая при этом модель может оказаться слишком громоздкой, сложной, ее информационное обеспечение (поиск, определение коэффициентов модели) весьма трудоемким, так, что разработка такой модели будет нецелесообразной. Однако, важно методологическое значение этого подхода, позволяющего оценить состояние объекта с помощью уравнений, учитывающих общие фундаментальные законы природы. А эти законы, как правило, отражают и управляют процессами и явлениями в природе и технике.
В зависимости от физической природы процессов, протекающих в системе агрегатов, и характера решаемой задачи математическая модель может включать уравнения баланса массы и энергии для всех подсистем модели, уравнения кинетики химических реакций, фазовых переходов, переноса вещества и энергии, а также теоретические и эмпирические соотношения между различными параметрами модели и ограничения на условия протекания процесса. Таким образом, детерминированные модели, применяемые для анализа и управления агрегатами, связывают входные параметры процесса x = {x1, x2, …, xn}, называемые воздействиями, с выходными характеристиками y = {y1, y2, …, ym} в виде уравнения связи [82]:
y = f(x), (1.1)
где x, y – векторы входных и выходных параметров. Соотношение (1.1) является математической моделью процесса, описывающего происходящие в системе изменения, если доказано подобие натурного и моделирующего процессов.
Детерминированные модели часто не подходят для моделирования сложных технологических систем. Во-первых, как правило, не удается в виде уравнений описать все существенные стороны сложных процессов. Во-вторых, рабочие характеристики одинаковых систем оказываются на практике неодинаковыми вследствие влияния многих неконтролируемых факторов, таких, например, как различие в условиях работы, вызванное износом различных агрегатов или деталей, колебанием свойств сырья и т.п.
Таким образом, в промышленных условиях, когда на состояния технологических агрегатов одновременно воздействует большое число параметров, важную роль играют случайные воздействия. Для описания таких агрегатов рассмотрим любой реальный процесс, которому свойственны случайные колебания, например, вызываемые физической изменчивостью каких-либо факторов xi + xi(τ) или внешними случайными воздействиями. В силу этого при равном среднем значении входных характеристик x(τ) в моменты τ1 и τ2 выходные параметры y(τ) будут неодинаковыми, поэтому для таких стохастических (вероятностных) процессов, где нельзя пренебречь случайными колебаниями Δxi(τ) по сравнению c xi(τ) и случайными внешними воздействиями ξi(τ), необходимо характеризовать систему с учетом статистического закона распределения мгновенных значений y(τ) относительно средней величины yср(τ) уравнением:
y(τ) = yср(τ) + Δy(τ) = f(yср) + ξ(Δx, ξ). (1.2)
Модели типа (1.2), отображающие случайный характер параметров и факторов объекта, называют стохастическими. По мере уменьшения величины параметров Δx и ξ уравнение (1.2) непрерывно приближается по структуре к уравнению (1.1), описывающему детерминированные системы. То есть статистические модели являются более широким классом моделей и включают детерминированные модели как предельный частный случай, в котором выходные переменные y однозначно определяются входными переменными x.
Построение и исследование статистической математической модели включает разработку, оценку качества и исследование поведения системы с помощью некоторого уравнения или системы уравнений, описывающих моделируемый агрегат. В этом случае исходная информация добывается на основе экспериментально–статистического подхода, путем проведения специального эксперимента с реальной системой, для чего созданы методы подготовки и проведения такого эксперимента, обработки результатов, а также критерии оценки полученных моделей. Этот подход эквивалентен известной проблеме исследования «черного ящика», т.е. речь может идти о построении математической модели на уровне статистической информации, описывающей поведение объекта.
С целью максимального извлечения информации из проводимых экспериментов и уменьшения их числа производится планирование экспериментов, т.е. выбор количества и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с заданной точностью.
Для построения статистической модели применяют два вида экспериментов: пассивный и активный [82]. Первый вид эксперимента за счет длительного и пассивного наблюдения за ходом процесса позволяет собрать обширный ряд данных для последующего статистического анализа. При активном эксперименте, имеется возможность регулирования условий проведения опытов. Причем наиболее эффективно одновременное варьирование величины всех факторов по определенному плану, при этом удается выявить взаимодействие факторов и существенно сократить объем экспериментов. Специальные вопросы проведения экспериментов и обработки их результатов при поиске оптимума рассматриваются в [61].
Таким образом, можно сделать вывод, что основным достоинством статистических моделей является их простота, позволяющая широко применять такие модели в системах автоматизированного управления сложными технологическими объектами. В ряде случаев статистические модели являются наиболее эффективным средством построения математической модели процесса, когда система уравнений для сложной системы оказывается слишком громоздкой, а целью моделирования является оперативное прогнозирование и управление процессом.
Однако эти модели имеют и существенные недостатки. Прежде всего, статистические модели недостаточно содержательны. В рамках этих моделей не вскрываются свойственные объекту глубокие причинно-следственные связи, а потому не учитывается все многообразие появлений процессов, протекающих в объекте, влияние различных внешних факторов на эти процессы. Кроме того, в статистических моделях отсутствует физическое обоснование взаимосвязи параметров и содержание различных коэффициентов, а экстраполяция полученных результатов за пределы границ проведенного эксперимента является неправомерной. В результате существенно ограниченной оказывается универсальность таких моделей.
Одной из сложных проблем, которая возникает при математическом моделировании и принятия решений по оптимальному управлению сложными производственными объектами является то, что исходная информация, которую реально удается собрать для решения указанных задач может оказаться нечеткой т.е. носит нечисловой характер. Такая проблема связана с тем, что большинство сложных объектов нефтеперерабатывающего производства, как правило, количественно трудноописываемы, а специальные средства сбора и обработки статистических данных в промышленных условиях недостаточны, не обладают необходимыми качествами или отсутствуют. Для разработки математического описания и моделирования таких объектов, рассмотренные выше, традиционные подходы (детерминированные, экспериментально-статистические), нецелесообразны, так как они требуют теоретических сведений или количественных, статистических данных и не дают существенных результатов.
В связи с этим, для повышения эффективности методов математического моделирования и принятия решений при исследовании и управлении количественно трудноописываемыми технологическими объектами нефтепереработки, необходимо обоснованное использование и формализация априорной качественной информации об особенностях функционирования этих объектов, что позволяет преодолеть проблем неопределен6ности. Эффективную формализацию качественной информации, представляющую собой знания, суждения специалистов-экспертов об исследуемом объекте, можно осуществлять на основе методов теории нечетких множеств (ТНМ), математический аппарат которой описан в работах [40–42, 83–86].
На практике опытный человек – оператор в состоянии управлять технологическими объектами в нечеткой среде, основываясь на некоторой модели качественного характера, формируемой в его сознании в процессе обучения и наблюдения за функционированием объекта. На основе методов экспертных оценок и теорий нечетких множеств можно получить формализованную модель такого объекта, не прибегая к помощи сложных математических структур, а основываясь на способности человека выразить его сущность в нечетких терминах естественного языка. Простейшей моделью этого типа будут выражения «если на вход системы подать 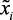 , то на выходе ее получим
, то на выходе ее получим 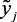 », где
», где 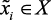 и
и 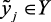 – некоторые термы из терм-множества T(Х, У). Далее, обрабатывая полученную качественную информацию методами теории нечетких множеств и возможностей, получим количественную оценку или модель этого объекта, используемую в процессе принятия решений. Разработанный при выполнении данной исследовательской работы метод синтеза математических моделей в нечеткой среде и результаты алгоритмизации его опубликованы в работах [87–89] и рассматриваются в разделе 2.
– некоторые термы из терм-множества T(Х, У). Далее, обрабатывая полученную качественную информацию методами теории нечетких множеств и возможностей, получим количественную оценку или модель этого объекта, используемую в процессе принятия решений. Разработанный при выполнении данной исследовательской работы метод синтеза математических моделей в нечеткой среде и результаты алгоритмизации его опубликованы в работах [87–89] и рассматриваются в разделе 2.
Таким образом, применение математического аппарата теории нечетких множеств и возможностей позволяет построить более простые и эффективные модели и алгоритмы решения задач принятия решений при управлении технологическими объектами в условиях неопределенности, когда применение традиционных подходов нецелесообразно или невозможно.
Наряду с эффективностью применения теории нечетких множеств следует отметить некоторые проблемы, которые возникают при ее практическом применении: неформализуемость задач построения функции принадлежности; сложность получения и систематизации первичной качественной информации; необходимость дополнительной проверки достоверности информации; трудность выбора решающих правил, представляемых в виде условных предложений для синтеза алгоритма принятия решений.
В прикладных и теоретических аспектах теории нечетких множеств возникают трудности, связанные с содержательной интерпретацией функций принадлежности и способов их построения. Интерпретацию понятия «Функция принадлежности» необходимо давать из реальной основы этого понятия, его источников в реальных процессах. Вопросы интерпретации функций принадлежности при различных постановках обсуждены в работах [90–92], по которым можно выделить лингвистические и вероятностные варианты интерпретации. Между тем, с целью повышения объективности анализа ситуаций целесообразно вести учет в одной модели как можно большего количества разнородной информации и, соответственно, характеристик ее размытости.
В работах [93, 90] рассмотрены методы построения функций принадлежности. Процесс построения функций принадлежности предполагает, что специалисты-эксперты обладают некой объективной информацией об исследуемом процессе. Тот факт, что функция принадлежности содержит элементы субъективизма, отражает методологию теории нечетких множеств. Дело в том, что именно несостоятельность подхода, основанного на использовании количественных (статистических) данных для исследования и управления сложными системами, и вызвала необходимость в создании теории, которая позволила бы формализовать в строгую математическую модель качественную информацию на обычном языке людей. При этом из-за сложности исследуемых систем, что существенно снижает достоверность получаемой информации, возникает необходимость в том, чтобы вложить качественное знание специалистов о процессе, пусть даже грубо отражающих истинный характер функционирования.
На практике при построении моделей реальных промышленных агрегатов приходится использовать комбинированный подход, который по возможности сочетает универсальность теоретического, простоту экспериментально-статистического подхода и возможность учета дополнительной качественной информации на основе методологии теории нечетких множеств. При этом возможны различные варианты объединения этих подходов. Например, для оценки состояния объекта используются уравнения, описывающие общие законы сохранения, а отдельные коэффициенты модели определяются экспериментально-статистическим методом.
Для оценки результатов работы производственных объектов используются, как правило, вектор критериев, которые могут быть и нечеткими. На основе этих критериев осуществляется принятия решений по выбору оптимального режима работы технологического объекта [95]. При этом задачи сводятся к минимизации или максимизации критериев. Ясно, что если критерием качества являются производительность, прибыль, выход целевых продуктов и другие технико-экономические показатели и экологические требования, то решается задача улучшения этих показателей.
Математические модели технологической установки будем характеризовать конечной совокупностью параметров, которые условно можно разделить на три группы: внутренние, внешние и выходные.
Под внутренними параметрами понимаются параметры, характеризующие протекания процесса, например, режимные параметры объекта. Внешние параметры характеризуют влияние внешней среды на оптимизируемый объект. Выходные параметры отражают основные свойства и характеристики оптимизируемой системы, например технико-экономические и экологические показатели производства.
Не все внутренние параметры являются равноправными: обычно только часть из них может варьироваться в процессе оптимизации. Изменяемые внутренние параметры называются управляемыми параметрами или параметрами оптимизации и образуют вектор
х = (х1, х2, …, хn). При отсутствии факторов неопределенности все внешние и неизменяемые внутренние параметры принимают известные, заранее заданные значения. В результате получается детерминированная модель, которая используется для алгоритмической оптимизации режимов работы технологического объекта [96].
Рассмотрим основу процесса принятия решений (ПР) для выбора оптимального режима работы технологических объектов нефтепереработки в условиях многокритериальности [97–100].
Принятие решений заключается в оценке возможных вариантов решений (альтернатив) и выбор наилучшего из них по заданным критериям. Реализация любого варианта решений предполагает наступление некоторых последствий, анализ и оценка которых, как правило, по нескольким (векторному) критериям эффективности полностью характеризует этот вариант решений. Задача ПР возникает, когда присутствует несколько вариантов действии (альтернатив) для достижения заданного или желаемого результата. При этом требуется выбрать наилучшую в определенном смысле альтернативу. Решение задач ПР сводится к выявлению и исследованию предпочтений лица, принимающего решения (ЛПР), а также построению на этой основе адекватной модели выбора наилучшей в некотором смысле альтернативы.
Общую постановку задачи ПР, понимаемой нами как задачу выбора оптимального режима работы объекта из некоторого допустимого множества альтернатив (вариантов решения – режимы работы объекта), можно сформулировать следующим образом.
Пусть Х – множество режимов работы объекта (альтернатив), Y – множество возможных последствий ПР (исходов, результатов). Х, Y – вообще говоря, произвольные абстрактные множества. Предполагается существование причинной связи между выбором некоторой альтернативы xi ∈ X и наступлением соответствующего исхода yi ∈ Y. Кроме того, предполагается наличие механизма оценки качества такого выбора, в качестве которого обычно выступает качество исхода.
Задача ПР может быть проиллюстрирована с помощью рис. 1.1.
Перейдем к анализу сформулированной задачи ПР. Первый важный момент заключается в определении характера связи альтернатив с исходами. Как мы видели из примеров, эта связь может быть детерминистской (или, как часто говорят, детерминированной). В этом случае существует однозначное отображение
 (1.3)
(1.3)
т.е. реализуется функция y = φ(x), x ∈X, y ∈ Y.
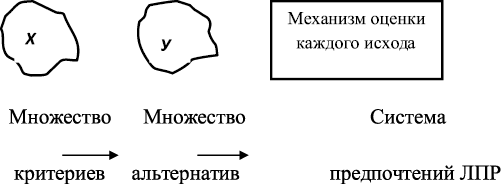
Рис. 1.1. Иллюстрация задачи ПР
Эта же связь может иметь вероятностный характер, когда выбор х определяет некоторую плотность распределения вероятностей на множестве Y. В этом случае выбор xi уже не гарантирует наступление определенного исхода yi, а сама задача ПР называется задачей ПР в условиях риска.
Характерная особенность процесса принятия решений при управлении производственными объектами, в которых особая роль принадлежит человеку, состоит не только в необходимости использования компьютерных систем, но и в привлечении суждений руководителей, специалистов – ЛПР [101]. Информация, получаемая на основе суждений ЛПР, позволяет выявить его предпочтения относительно значений критерия, при составлении значений различных критериев и очень важна для выбора решения.
Целью принятия решений является перевод состояния объекта в текущий момент времени в некоторую желаемую область состояния. При этом должны быть созданы условия, обеспечивающие данный перевод. Для производственных объектов обычно стремятся к достижению экстремального значения, как правило, нескольких критериев, при котором выполняется целенаправленное изменение состояния объекта в желаемую область, зависящее от конкретной ситуации, сложившейся на производстве в текущий момент времени.
Таким образом, принятие решений определяется отличием между фактическим и желательным состоянием объекта, степенью информированности ЛПР о состоянии и целях функционирования объекта. При конкретизации проблемы принятия решений определяют средства, ресурсы и параметры, которые надо изменять для достижения желаемой области, т.е. формулируют задачу ПР.
В общем виде задачу ПР можно записать в виде:
<Задачи ПР> = {дано V, VS, VP, требуется обеспечить W}, (1.4)
где V – заданные условия; VS – множество возможных состояний объекта; VP – множество возможных операторов, которые обеспечивают переход объекта из одного состояния в другое; W – желаемое состояние объекта.
При этом решение задачи ПР заключается в выборе последовательности операторов для перевода объекта из состояния в текущий момент в желаемое состояние.
В зависимости от поставленной задачи ПР и сложности объектов можно выделить два основных метода: целостный выбор, когда ЛПР оперирует непосредственно с альтернативами, и критериальный-экспертный выбор, – когда ЛПР формирует множество критериев и ограничений, назначает правило выбора, а оценку критериев получает в результате моделирования или взаимодействия с системой, при этом часть альтернатив оценивается экспертами. Практическое использование первого метода весьма ограничено для сложных объектов, какими являются производственные, так как ЛПР оперативно оперирует ограниченным количеством информации (7 ± 2 структурных единиц информации – альтернатив).
Многомерность, качественные различия критериев, возможная неопределенность модели производственных систем в сочетании с нечеткостью служат серьезным препятствиями при получении оценки качества объекта и вызывает необходимость рассмотрения более общих подходов к понятию оптимальности, т.е. развития и разработки новых методов в теории принятия решений для многокритериальных нечетких задач. Интенсивному развитию этой теории способствовало широкое и эффективное применение компьютерной технологии, позволяющая проводить анализ и обработку больших массивов данных.
Многие задачи ПР имеют следующую характерную особенность: модель, описывающая множество допустимых решений, объективна, но качество решения оценивается по многим критериям. Для выбора наилучшего варианта решения необходим компромисс между оценками по различным критериям. В условиях задачи отсутствует информация, позволяющая найти такой компромисс. Следовательно, он не может быть определен на основе объективных расчетов [102].
Рассмотрим проблемы многокритериальности при принятии решения. Многокритериальные задачи ПР возникают тогда, когда требуется выбрать решение лучшее сразу по нескольким противоречивым локальным критериям. Так, в задачах управления производством обычно необходимо максимизировать выход целевых продуктов с требуемыми показателями качества, при ограниченных затратах, издержках и потерях. Поскольку решения, лучшего одновременно по всем критериям, обычно нет, необходим разумный компромисс. Так как только человек (ЛПР) может знать, какие показатели более важны, то решение многокритериальных задач должно строиться на базе информации о предпочтениях ЛПР.
При появлении многих критериев задачи выбора наилучшего решения приобретают следующие особенности:
● задача имеет уникальный, новый характер – нет статистических данных, позволяющих обосновать соотношения между различными критериями;
● на момент принятия решения принципиально отсутствует информация, позволяющая объективно оценить возможные последствия выбора того или иного варианта решения. Но поскольку решение, так или иначе, должно быть принято, то недостаток информации необходимо восполнить. Это может быть сделано лишь людьми на основе их опыта и интуиции.
В многокритериальных задачах часть информации, необходимой для полного и однозначного определения требований к решению, принципиально отсутствует. Исследователь часто может определить основные переменные, установить связи между ними, т. е. построить модель, адекватно отражающую ситуацию. Но зависимости между критериями вообще не могут быть определены на основе объективной информации, имеющейся в распоряжении исследователя. Такие проблемы являются слабоструктурированными, так как здесь недостаток объективной информации принципиально неустраним на момент принятия решения.
Проблемы многокритериального выбора при нечеткой исходной информации стали предметом исследования ученых относительно недавно. Наиболее интенсивные разработки в этом направлении начаты в Рижском политехническом институте в трудах А.И. Борисова и др. [103,104]. Главным «узким местом» на пути широкого применения разработанных подходов и алгоритмов решения многокритериальных задач ПР в нечеткой среде является свертывание (преимущественно линейное) векторного критерия эффективности и векторных нечетких отношений предпочтений. К другим недостаткам данных подходов, препятствующим их применению при решении задач управления производством, относятся:
● использование понятия «нечеткости» в основном только тогда, когда речь идет об отношениях предпочтения (в смысле степени превосходства одного варианта над другим);
● попытки вычисления строгого нечеткого отношения предпочтения без учета мнений ЛПР;
● недостатки проработки вопросов человеко-машинного взаимодействия при формализации и решении задач ПР, низкий уровень «интеллектуальности» интерфейса пользователя и программно-алгоритмического обеспечения человеко-машинных систем для решения этих задач.
Существуют проблемы, в которых известен только перечень основных параметров, но количественные связи между ними установить нельзя (нет необходимой информации). Иногда ясно лишь, что изменение параметра в определенных пределах сказывается на решении. В таких случаях структура, понимаемая как совокупность связей между параметрами, не определена, и проблема называется неструктуризованной. Слабоструктурированные и неструктурированные проблемы исследуются в рамках научного направления, называемого принятием решений при многих критериях.
В зависимости от известности исходного множества альтернатив – Ω и принципа оптимальности – 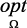 , задачи ПР классифицируется:
, задачи ПР классифицируется:
● общая задача принятия решений – Ω и 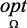 неизвестны;
неизвестны;
● задача выбора – Ω известно, 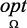 неизвестен;
неизвестен;
● общая задача оптимизации – Ω и 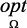 – известны.
– известны.
Задачи ПР в зависимости от соотношения между ситуациями, альтернативами и исходами принятых решений разделяются на: задачи ПР в условиях определенности, риска и в нечеткой среде.
Задачи ПР в условиях определенности (детерминированные задачи ПР) характеризуются однозначной детерминированной связью между альтернативами Xi и исходом S. Предполагается, что известны исходное множество альтернатив Ω = {Xi} и однозначные оценки исхода S в виде свойств альтернативы Xi, описываемых, как правило, несколькими критериями f1(xi), f2(xi), …, fm(xi), f(xi) назовем векторным критерием.
В этих случаях задача ПР формализуется как задача выбора (векторной оптимизации):
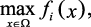
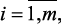 x = (x1, x2, …, xn). (1.5)
x = (x1, x2, …, xn). (1.5)
В таком виде, задача (2) не является корректной и отражает только стремление сделать значение локальных критериев побольше. В этих задачах необходимо уточнять понятие оптимальности. Это понятие должно быть, с одной стороны, близким к представлению об оптимальности ЛПР, а с другой стороны достаточно формализуемым, чтобы с ним можно было работать алгоритмически, а не интуитивно. Принцип оптимальности задает понятие лучших альтернатив.
Разные методы решения таких многокритериальных задач ПР отличаются способом агрегирования оценки по отдельным критериям в общую. К основным методам решения можно отнести:
● прямые методы, в которых зависимость общей оценки от оценок по частным критериям выбирается заранее тем или иным способом, например с помощью ЛПР;
● методы компенсации, – основаны на идее компенсации оценки одной альтернативы оценками другой, чтобы найти какие альтернативы лучше. По идее, это наиболее простой метод, при котором ЛПР выписывает достоинства и недостатки каждой из альтернатив и, вычеркивая попарно эквивалентные достоинства (недостатки), изучает оставшиеся оценки по критериям;
● методы порогов сравнимости, здесь задается правило сравнения двух альтернатив, при котором одна альтернатива считается лучше другой. В соответствии с заданными правилами альтернативы попарно делятся на сравнимые (лучшие, эквивалентные) и несравнимые. При изменении условии меняется количество сравнимых альтернатив. При этом меняется состав так называемого ядра (например, множество Парето), куда входят альтернативы, оказавшиеся не худшими при всех сравнениях, т.е. выделяются лучшие решения;
● аксиоматические методы, в которых определяется ряд аксиомы, которым должна удовлетворять зависимость общей полезности от оценок по локальным критериям. Эти аксиомы (свойства) проверяются путем получения информации от ЛПР, в соответствии с которой делается вывод о той или иной форме зависимости;
● человеко-машинные (диалоговые) методы применяются в том случае, когда модель проблемы известно частично. ЛПР взаимодействуют с ЭВМ, определяя соотношения между локальными критериями, он сначала определяет первоначальные требования к соотношениям критериев, вводит в ЭВМ, получает реальные значения критериев, изменяет свой требования, снова вводит в ЭВМ и т.д. В ходе таких итераций ЛПР проясняет характерные черты задачи, выявляет и уточняет свои предпочтения и в результате сообщает дополнительную информацию, благодаря которой ЭВМ вырабатывает все более совершенные решения. Такой диалог между ЛПР – ЭВМ, при наличии удобного для пользователя интерфейса, способствует выработке разумного компромисса в требованиях ЛПР к значениям, достигаемым
по разным критериям.
Стохастические задачи принятия решений (задачи ПР при риске) возникают в тех случаях, когда с каждым принимаемым решением xI ∈ Ω связано множество исходов из m возможных результатов S1, …, Sn с известными вероятностями P(Sj|xi), 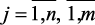 , т.е. в этих задачах нет однозначной связи между альтернативами и исходом. При P(Sj|xi) = 1, задачи ПР при риске и детерминированные задачи ПР совпадают.
, т.е. в этих задачах нет однозначной связи между альтернативами и исходом. При P(Sj|xi) = 1, задачи ПР при риске и детерминированные задачи ПР совпадают.
Для решения задач ПР при риске широко применяются методы теории стохастического программирования, игр, массового обслуживания и другие вероятностные методы. Пусть определены lij = f(Sj|xi) – функция полезности исхода Sj при принятии решений xi и P(Sji|xi) и P(Sj|xi) – условные вероятности, характеризующие переход объекта в состояние Sj при использовании стратегии xi, тогда полезность каждого решения представляется в виде:
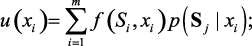
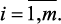
В этом случае выбор решения осуществляется по следующему правилу, обеспечивающему достижение максимального значения ожидаемой полезности:
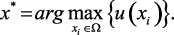
Задачи ПР в нечеткой среде. Будем полагать, что в ситуациях принятия решений, когда хотя бы один из элементов задачи (альтернативы, критерии, предпочтения и ограничения) описывается нечетко имеют место задачи ПР в нечеткой среде (при нечеткой исходной информации). В данной научной работе в основном исследуются именно такие задачи ПР.
Перспективным направлением разработки методов ПР в нечеткой среде является лингвистический подход на базе теории нечетких множеств. К настоящему времени в этом направлении получены конкретные практические результаты. Однако некоторые ситуации, сложившиеся на производстве в условиях неопределенности, требует новых подходов к формализации задач ПР и разработку методов их решения.
Разработанные в данной работе методы и алгоритмы решения задач ПР в нечеткой среде, а также примеры их реализации рассматриваются в разделе 3.
Таким образом, на практике при моделировании и принятия решений по управлению производственными объектами по многим критериям (экономико-экологического характера) необходимо разработать и применить методы работоспособные в условиях многокритериальности и неопределенности, вызванной дефицитом, случайностью и нечеткостью исходной информации.
