
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.1. Формализация и математическая постановка задач многокритериальной оптимизации технологического комплекса в нечеткой среде на примере блока риформинга
Результаты работы производственных объектов оцениваются некоторыми показателями – локальными критериями экономического, экологического, технологического и др. характера. Для оптимального управления такими объектами требуется эти критерии обратить в экстремум (максимум или минимум). Такие задачи формализуются в виде многокритериальных задач принятия решений (ПР), которые решаются на основе математических моделей управляемого объекта.
Из-за большого количества и многообразия параметров, определяющих течение процессов каталитического риформинга, из-за внутренних связей между параметрами технологического комплекса, из-за математически неформализуемого действия человека-оператора эти объекты и их оптимизации являются сложными. Кроме того, при решении задач принятия решений по управлению такими объектами часто возникает ряд проблем, связанных с множеством противоречивых и нечетко описываемых критериев, определяющих качество работы объекта. В этих случаях при решении задач ПР основными источниками информации станут человек (специалисты-эксперты, ЛПР, технолог, оператор блока) т.е. его знания, опыт, интуиция и суждения, которые выражаются качественной информацией, т.е. словесно.
Рассмотрим подход к формализации и постановку задач ПР в условиях рассмотренных проблем – многокритериальности и неопределенности, вызванной нечеткостью доступной информации. Конкретизируем формализацию и постановку задач оптимизации на основе математических моделей на примере принятия решений по управлению технологическим комплексом блока каталитического риформинга, описанного в предыдущем разделе.
Пусть f(x) = f1(x), …, fm(x) вектор критериев, оценивающий качество работы, например, экономическую эффективность и экологическую безопасность технологического комплекса блока риформинга. Например: f1(x), f2(x), f3(x) – соответственно, выход целевого продукта – объем катализата, сухого газа и ВСГ (водород содержащий газ); f4(x), f5(x), …, f14(x) – качественные показатели выходных продуктов (например, для катализата – бензина: октановое число; фракционный состав по ГОСТу 2177-82 – 10 и 50 % отгонка; давление насыщенных паров; содержание фактических смол, содержание водорастворимых кислот и щелочей; для сухого газа: содержание водорода, метана, этана, пропана, изобутана и н-бутана; для ВСГ: водород в % об.; удельный вес), f15(x), f16(x), …, f23(x) – локальные критерии оценок экологической безопасности, например, твердые, жидкие и газообразные отходы и выбросы (отработанные катализаторы, сточные воды, выбросы в атмосферу – УВ газы, сероводород, сернистый ангидрид, окись углерода, двуокись азота, сажа), а также ущерб от загрязнения окружающей среды нефтепродуктами и отходами переработки [113].
Каждый из m критериев зависит от вектора n параметров (управляющих воздействий, режимных параметров) x = (x1, …, xn), например: температуры и давления реакторов, печи и др.; состава сырья, характеристик катализаторов и т.д. Эту зависимость описывают модели, разработанные в предыдущем разделе. На практике всегда имеются различные ограничения (экономические, технологические, экологические), которые можно описать некоторыми функциями – ограничениями jq ≥ bq, 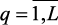 . Следует отметить, что некоторые из рассмотренных локальных критериев и ограничений сводятся к качественным ограничениям вида не более или не менее чем bq
. Следует отметить, что некоторые из рассмотренных локальных критериев и ограничений сводятся к качественным ограничениям вида не более или не менее чем bq 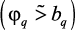 . Режимные, управляющие параметры также имеют свои интервалы изменения, задаваемые технологическим регламентом установки:
. Режимные, управляющие параметры также имеют свои интервалы изменения, задаваемые технологическим регламентом установки: 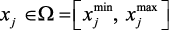 ,
, 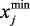 ,
, 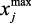 – нижний и верхний пределы изменения параметра xj. Эти ограничения могут быть нечеткими
– нижний и верхний пределы изменения параметра xj. Эти ограничения могут быть нечеткими 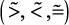 . Требуется выбрать оптимальное решение – режим работы блока риформинга, обеспечивающее экстремальное значение вектора критериев при выполнении заданных ограничений и нечеткости некоторых исходных данных, а также учитывающее
. Требуется выбрать оптимальное решение – режим работы блока риформинга, обеспечивающее экстремальное значение вектора критериев при выполнении заданных ограничений и нечеткости некоторых исходных данных, а также учитывающее
предпочтения ЛПР.
Формализованную задачу в условиях многокритериальности и нечеткости можно записать в виде следующей задачи многокритериальной оптимизации:
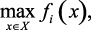
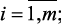 (3.1)
(3.1)
 (3.2)
(3.2)
Решением данной задачи является значение вектора режимных параметров 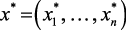 , обеспечивающее такие значения локальных критериев, которые удовлетворяют ЛПР.
, обеспечивающее такие значения локальных критериев, которые удовлетворяют ЛПР.
Если часть или все элементы приведенной задачи (критерии, ограничения, важность критериев и ограничений) описаны не количественной, а качественно (нечетко), то такая задача называется задачей ПР в условиях неопределенности на основе качественной информации. В известных методах решения таких задач, в основном, рассматриваются однокритериальные случаи, нет гибкости в учете предпочтений ЛПР [125]. При этом, как правило, нечеткая задача на этапе постановки заменяется эквивалентной детерминированной, что приведет к потере части информации.
Во многих случаях качественные факторы (нечеткие высказывания и суждения) являются основными и привычными для человека. Преобразование нечеткого описания в количественное не всегда удается или оказывается нецелесообразным. В связи с этим, в данной работе предложен наиболее перспективный подход, основанный на разработке методов ПР, приспособленных к человеческому языку, к качественным факторам любого характера, к человеческим процедурам принятия решений, которые ставятся и решаются в нечеткой среде, не преобразуя их к детерминированным задачам, т.е не теряя доступную информацию нечеткого характера [126].
Таким образом, сведем задачу (3.1)–(3.2) к многокритериальной задаче оптимизации с учетом лингвистической информации.
Пусть 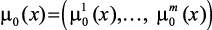 – нормализованный вектор критериев – fi(x),
– нормализованный вектор критериев – fi(x), 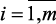 , оценивающий критерии управления блока каталитического риформинга. Допустим, что для каждого нечеткого ограничения
, оценивающий критерии управления блока каталитического риформинга. Допустим, что для каждого нечеткого ограничения 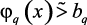 ,
, 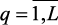 построена функция принадлежности его выполнения mq(x),
построена функция принадлежности его выполнения mq(x), 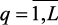 . Известен либо ряд приоритетов для локальных критериев Ik = {1, …, m} и ограничений Ir = {1, …, L}, либо весовой вектор, отражающий взаимную важность критериев (g = (g1, …, gm)) и ограничений (b = (b1, …, bL)).
. Известен либо ряд приоритетов для локальных критериев Ik = {1, …, m} и ограничений Ir = {1, …, L}, либо весовой вектор, отражающий взаимную важность критериев (g = (g1, …, gm)) и ограничений (b = (b1, …, bL)).
Тогда, например, на основе идеи методов главного критерия и максимина многокритериальную задачу ПР с векторным ограничениям с учетом качественного исходной информации (3.1)–(3.2) можно записать в следующей постановке [126]:
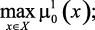 (3.3)
(3.3)
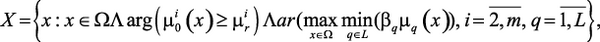 (3.4)
(3.4)
где L – логический знак «и», требующий, чтобы все связываемые им утверждения были истинны; 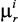 – граничные значения для локальных критериев
– граничные значения для локальных критериев 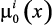 ,
, 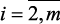 , задаваемые ЛПР. Область определения переменных х и выполнения нечетких ограничений определяется на основе принципа максимина (гарантированного результата).
, задаваемые ЛПР. Область определения переменных х и выполнения нечетких ограничений определяется на основе принципа максимина (гарантированного результата).
Меняя 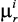 и вектор важности ограничений b = (b1, …, bL), получаем семейство решений задачи (3.3)–(3.4) – x*(mr, b). Выбор наилучшего решения можно осуществлять на основе диалога с ЛПР.
и вектор важности ограничений b = (b1, …, bL), получаем семейство решений задачи (3.3)–(3.4) – x*(mr, b). Выбор наилучшего решения можно осуществлять на основе диалога с ЛПР.
Алгоритм решения полученной задачи многокритериальной оптимизации (3.3)–(3.4) разработан и описан следующем подразделе.
Используя идеи методов Парето оптимальности и идеальной точки, модифицируя их на случай качественного характера исходной информации, многокритериальную задачу ПР (3.1)–(3.2) можно переписать в виде:
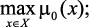 ,
, 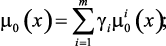 (3.5)
(3.5)
 (3.6)
(3.6)
где ||•||D – используемая метрика D; m(x) = (m1(x), …, mL(x)),
mu = (max m1(x), …, max mL(x)). Возможен вариант использования в качестве координат идеальной точки mu единиц: mu = (1,…,1); g = (g1, …, gm) – весовой вектор, отражающий взаимную важность локальных критериев.
Модифицируя использованных компромиссных схем при постановке задачи (3.5)–(3.6), нами предложен алгоритм ее решения, который описан в 3.2.
Используя идею принципов абсолютной (относительной) уступки и Парето оптимальности в условиях нечеткости, можно поставить следующую многокритериальную задачу оптимизации с несколькими ограничениями:

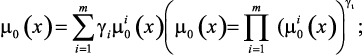
или
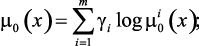 (3.7)
(3.7)
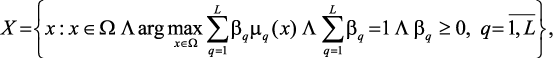 (3.8)
(3.8)
где L – логический знак «и», требующий, чтобы все связываемые им утверждения были истинны, g = (g1, …, gm) и b = (b1, …, bL) – соответственно, весовые векторы, отражающий взаимную важность критериев и ограничений.
Таким образом, в данном разделе формализованы различные задачи многокритериальной оптимизации по оптимальному управлению режимами работы технологического комплекса нефтепереработки на примере блока каталитического риформинга в условиях неопределенности. На основе компромиссных схем и методов теории возможностей задачи поставлены в виде многокритериальных задач оптимизации в нечеткой среде, которые являются одним из новизны результатов данной работы. На основе этих результатов получены конкретные задачи принятия и выбора оптимальных режимов работы технологических агрегатов блока каталитического риформинга.
