
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.1. Проблемы моделирования и оптимизации при управлении производственными объектами
Определение качества функционирования технологических объектов любого производства, в т.ч. нефтепереработки, определение оптимальных режимных параметров, выбор эффективной структуры и алгоритмов поведения, в соответствии с поставленной целью – основные проблемы при управлении функционирующими объектами и проектировании современного производства. Многокомпонентность, большая размерность, многопараметричность и неопределенность в производственных условиях усложняют решению указанных проблем. Методы математического моделирования и принятия решений являются научно обоснованными эффективными подходами к решению этих сложных проблем производства. Однако при применении методов моделирования и принятия решении в процессе управления производством возникают определенные проблем научного и практического характера. Рассмотрим этих проблем и подходов к их решению.
Методы математического моделирования в сочетании с современными вычислительными средствами позволяют с высокой точностью быстро исследовать различные варианты функционирования производственной системы, изучить ее основные особенности и вскрыть резервы усовершенствования. При математическом моделировании процесс исследуют, изменяя различные параметры, связанные в виде математической модели, на компьютере. Это позволяет быстро получать сведения о различных вариантах изучаемого процесса и определить оптимальных условий протекания технологических и производственных процессов, управление им на основе математической модели и перенос результатов на объект.
В основе любого вида моделирования лежит некоторая модель, имеющая соответствие, базирующееся на некотором общем качестве, которое характеризует реальный объект. Объективно реальный объект обладает некоторой формальной структурой, поэтому для любой модели характерно наличие некоторой структуры, соответствующей формальной структуре реального объекта, либо изучаемой стороне этого объекта.
В производственных условиях в качестве объекта моделирования выступают сложные организационно-технические системы, которые можно отнести к классу больших систем. Более того, по своему содержанию и созданная модель М также становится системой S(M) и тоже может быть отнесена к классу больших систем.
Одним из наиболее важных аспектов построения систем моделирования является проблема цели. Любую модель строят в зависимости от цели, которую ставит перед ней исследователь, поэтому одна из основных проблем при моделировании – это проблема целевого назначения. Подобие процесса, протекающего в модели М, реальному процессу является не целью, а условием правильного функционирования модели, и поэтому в качестве цели должна быть поставлена задача изучения какой-либо стороны функционирования объекта.
Если цель моделирования ясна, то возникает следующая проблема, а именно проблема построения модели М. Построение модели оказывается возможным, если имеется информация или выдвинуты гипотезы относительно структуры, алгоритмов и параметров исследуемого объекта. На основании их изучения осуществляется идентификация объекта. В настоящее время широко применяют различные способы оценки параметров (метод наименьших квадратов, метод максимального правдоподобия, байесовские, Марковские оценки и т.д.).
При построении модели производственных объектов возникают проблемы дефицита информации, неопределенности и нечеткости исходной информации. Для решения проблем неопределенности, вызванной случайным характером параметров моделируемого объекта, применяются вероятностные методы. Следует отметить, что эти методы применимы только в определенных условиях – при выполнении аксиом теории вероятностей (статистическая устойчивость объекта, многократная воспроизводимость результатов эксперимента в одинаковых условиях).
Особенностью большинства производственных объектов и процессов нефтепереработки, в которых участвует человек, является их сложность, вызванной не только значительным числом и многообразием параметров, но и неформализуемым действием человека, участвующего в контуре управления. В этих условиях при исследовании объектов и построении их математических моделей возникает проблема неопределенности, связанная с нечеткостью – качественного характера исходной информации, которую реально удаётся собрать для моделирования исследуемого объекта. Такая проблема связана с тем, что обычно сложные объекты количественно трудноописываемы, а специальные средства сбора и обработки необходимых статистических данных в промышленных условиях недостаточны, не обладают необходимыми свойствами или отсутствуют. В этих ситуациях часто единственным источником информации является человек (производственный персонал, специалист-эксперт), который сможет формализовать свои знания, опыт, интуицию (информацию) на естественном языке (словесно) в виде суждений, логического вывода, т.е. собранная информация носит качественный характер.
Попытки распространения традиционных методов моделирования на количественно трудноописываемые объекты (технологические установки нефтепереработки) пока не дали хороших результатов, несмотря на существенное развитие математических методов, а также средств вычислительной техники. На практике такими объектами и процессами достаточно хорошо управляет человек (оператор-технолог, руководитель). Человек в таких случаях довольно успешно справляется с неопределённостью и сложностью процесса управления. В отличие от машины, человек использует нечёткие качественные понятия и довольно успешно ориентируется в сложной обстановке. В связи с этим, возникает задача, как передать способности человека машине для моделирования и управления сложными промышленными объектами и производственными процессами. Для решения такой задачи требуются специальные методы формализации нечёткости и обработки размытой, качественной информации. Из различных методов решения этих задач в качестве наиболее эффективного можно выделить методы теории нечетких множеств и возможностей, которые используются в комбинации методами экспертных оценок. Именно эти методы применены и развиты в данной работе при разработке моделей и принятия решений по управлению технологическими объектами нефтепереработки на примере блока риформинга установки ЛГ Атырауского НПЗ.
Если модель М построена, то следующей проблемой можно считать проблему работы с ней, т.е. реализацию модели, основные задачи которой минимизация времени получения конечных результатов и обеспечение их достоверности. Для правильно построенной модели М характерным является то, что она выявляет лишь те закономерности, которые нужно исследователю, и не рассматривает свойства системы S, несущественные для данного исследования.
Таким образом, характеризуя проблему моделирования в целом, необходимо учитывать, что от постановки задачи моделирования до интерпретации полученных результатов существует большая группа сложных научно-технических проблем, к основным из которых можно отнести следующие: идентификацию реальных объектов, выбор вида моделей, построение моделей и их машинную реализацию, взаимодействие
исследователя с моделью в ходе машинного эксперимента, проверку правильности полученных в ходе моделирования результатов, выявление основных закономерностей, исследованных в процессе моделирования. В зависимости от объекта моделирования и вида используемой модели эти проблемы могут иметь разную значимость [114, 142].
Процесс принятия управленческого решения – это преобразование исходной информации (информации состояния) в выходную информацию (информацию управления). Решение может быть формальным и творческим. Принято считать, что если преобразование информации выполняется с помощью математических моделей, то выработанное решение считается формальным, если решение появляется в результате скрытой работы интеллекта человека, принимающего решение, то оно – творческое.
Для ситуаций, в которых происходит выбор решений, характерны:
1. Наличие цели (целей): Необходимость принятия решения диктуется только наличием некоторой цели, которую следует достичь. Если цель отсутствует, то не возникает и необходимость принимать какое-либо решение.
2. Наличие альтернативных линий поведения: Решения принимаются в условиях, когда существует более одного способа достижения поставленной цели. Каждый из способов может характеризоваться различными степенями и различными вероятностями достижения цели, требовать различных затрат.
3. Наличие ограничивающих факторов: Естественно, что лицо, принимающее решение, не обладает бесконечными возможностями. Все множества ограничивающих факторов можно разбить на три группы: экономические факторы – денежные средства, трудовые и производственные ресурсы, время и т.п.; технические факторы – режимы работы, энергопотребление, надёжность, точность и т.п.; социальные факторы, учитывающие требования человеческой этики и морали.
Такое деление в достаточной степени условно, поскольку чисто формального или чисто творческого решения не существует. Если решение вырабатывается с помощью математической модели, то знания и опыт человека (элементы творчества) используются при её создании, а интуиция (тоже момент творчества) – в момент, когда он задаёт то или иное значение параметра исходной информации или выбирает из множества альтернативных вариантов, полученных с помощью математической модели, один в качестве решения на управление. Если основным инструментом выработки решения является интеллект человека, то формальные методы, носителем которых практически является вся наука, скрыто присутствуют в его знаниях и опыте.
В соответствии с подразделением на творческие и формальные всё множество проблем, сопутствующих любому процессу принятия решений, условно делится на два класса: проблемы концептуального характера и проблемы формально-математического и вычислительного характера.
К концептуальным проблемам относятся сложные логические проблемы, которые невозможно решить с применением только формально-математических методов и ЭВМ. Часто эти проблемы уникальны в том смысле, что они решаются впервые и не имеют прототипов в прошлом. Концептуальные проблемы обычно решаются на уровне руководителей с привлечением группы экспертов, в качестве которых выступают высококвалифицированные специалисты из различных областей науки и практической деятельности. При решении концептуальных проблем наибольший вес имеют не формально-математические методы, а эрудиция, опыт и интуиция людей. Формальные методы здесь играют вспомогательную роль как средство, облегчающее и организующее эвристическую деятельность людей. К числу концептуальных относятся, в частности, такие проблемы, как анализ и выбор целей, выявление совокупностей показателей, характеризующих следствия принятого решения, выбор из их числа критериев оптимальности и т.п. Формализация эвристических процедур является содержанием так называемой неформальной теории принятия решений.
Процесс принятия решений является сложной итерационной процедурой. Структурная схема процесса принятия решений может иметь вид приведенный на рис. 4.1.
Общая постановка задачи принятия решения
Пусть эффективность выбора того или иного решения определяется некоторым критерием F, допускающим количественное представление. В общем случае все факторы, от которых зависит эффективность выбора, можно разбить на две группы:
а) контролируемые (управляемые) факторы, выбор которых определяется лицами, принимающими решения. Обозначим эти факторы X1, X2, …, XL;
б) неконтролируемые (неуправляемые) факторы, характеризующие условия, в которых осуществляется выбор и на которые ЛПР, влиять не могут. В состав неконтролируемых факторов может входить и время t. Неконтролируемые факторы в зависимости от информированности о них подразделяют на три подгруппы: детерминированные неконтролируемые факторы – неслучайные фиксированные величины, значения которых полностью известны, A1, A2, …, AP.); стохастические неконтролируемые факторы – случайные величины и процессы с известными
законами распределений, Y1, Y2, …, Yg; неопределённые неконтролируемые факторы, для каждого из которых известна только область, внутри которой находится закон распределения, значения неопределённых факторов неизвестны в момент принятия решения, Z1, Z2, …, ZZ.
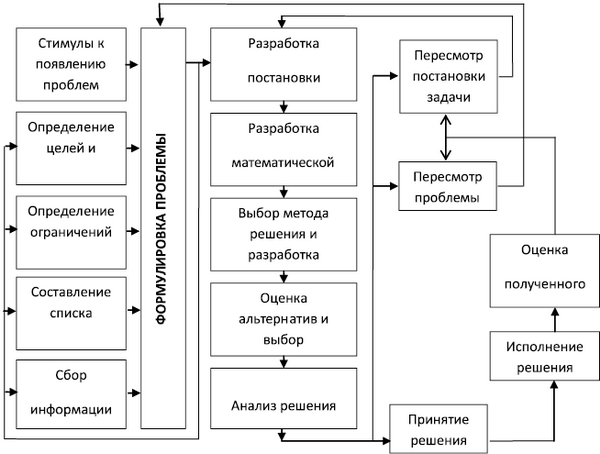
Рис. 4.1. Структурная схема процесса принятия решений
В соответствии с выделенными факторами критерий оптимальности можно представить в виде:
F = F(X1, X2, …, XL, A1, A2, …, AP, Y1, Y2, …, Yg, Z1, Z2, …, ZZ, t).
Значения контролируемых факторов обычно ограничены рядом естественных причин, например, ограниченностью располагаемых ресурсов. То есть определены (имеются) области Wx1, Wx2, …, WxL пространства, внутри которых расположены возможные (допустимые) значения факторов X1, X2, …, XL. Аналогично могут быть ограничены и области возможных значений неконтролируемых факторов. Величины X, A, Y, Z в общем случае могут быть скалярами, векто-
рами, матрицами.
Поскольку критерий оптимальности есть количественная мера степени достижения цели управления, математически цель управления выражается в стремлении к максимально возможному увеличению (или уменьшению) значения критерия F, что можно записать в виде: F → max (или min).
Средством достижения этой цели является соответствующий выбор управлений X1, X2, …, XL из областей Wx1, Wx2, …, WxL их допустимых значений. Таким образом, общая постановка задачи принятия решений может быть сформулирована так: при заданных значениях и характеристиках фиксированных неконтролируемых факторов A1, A2, …, AP, Y1, Y2, …, Yg, с учётом неопределённых факторов Z1, Z2, …, ZZ, найти оптимальные значения X1опт, X2опт, …, XLопт из областей Wx1, Wx2, …, WxL их допустимых значений, которые по возможности обращали бы в максимум (минимум) критерий оптимальности F.
Так как производственные задачи, прежде всего, характеризуются многокритериальностью, рассмотрим проблемы принятия решений в этих условиях.
Пусть, как и прежде, необходимо выбрать одно из множества решений X из области Wx их допустимых значений. Но, в отличие от рассмотренного ранее, каждое выбранное решение оценивается совокупностью критериев f1, f2, …, fk, которые могут различаться своими коэффициентами относительной важности (g1, …, gk). Критерии fq, 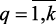 , называют частными или локальными критериями, они образуют интегральный или векторный критерий оптимальности F = {fq}. Коэффициенты (gq
, называют частными или локальными критериями, они образуют интегральный или векторный критерий оптимальности F = {fq}. Коэффициенты (gq 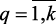 , образуют вектор важности G = (gq). Каждый локальный критерий характеризует некоторую локальную цель принимаемого решения.
, образуют вектор важности G = (gq). Каждый локальный критерий характеризует некоторую локальную цель принимаемого решения.
Оптимальное решение X должно удовлетворять соотношению:
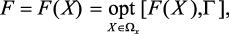
где F – оптимальное решение интегрального критерия; opt – оператор оптимизации, он определяет выбранный принцип оптимизации.
Область допустимых решений Wx может быть разбита на две непересекающиеся части: 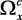 – область согласия, в которой качество решения может быть улучшено одновременно по всем локальным критериям или без снижения уровня любого из критериев;
– область согласия, в которой качество решения может быть улучшено одновременно по всем локальным критериям или без снижения уровня любого из критериев; 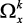 – область компромиссов, в которой улучшение качества решения по одним локальным критериям приводит к ухудшению качества решения по другим. Очевидно, что оптимальное решение может принадлежать только области компромиссов, так как в области согласия решение может и должно быть улучшено
– область компромиссов, в которой улучшение качества решения по одним локальным критериям приводит к ухудшению качества решения по другим. Очевидно, что оптимальное решение может принадлежать только области компромиссов, так как в области согласия решение может и должно быть улучшено
по соответствующим критериям. Выделение области компромисса сужает область возможных решений, но для выбора одного-единственного варианта решения необходимо выбрать схему компромисса, то есть раскрыть смысл оператора оптимизации opt. Этот выбор осуществляется субъективно.
Рассмотрим основные схемы компромисса, предполагая вначале, что все локальные критерии нормализованы (то есть имеют одинаковую размерность или являются безразмерными величинами) и одинаково важны. Рассмотрение удобно вести, перейдя от пространства Wx выбираемых решений X к пространству Wk возможных (допустимых) локальных критериев F = {f1, f2, …, fk}, деля его на область согласия и область компромиссов.
Тогда сформулированную ранее модель оптимизации можно переписать в виде:
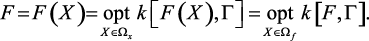
Основными схемами компромисса являются: принцип равномерности; принцип справедливой уступки; принцип выделения одного оптимизируемого критерия; принцип последовательной уступки и др. некоторые которых модифицированы и использованы нами в предыдущих разделах.
Принцип равномерности провозглашает целесообразность выбора такого варианта решения, при котором достигалась бы некоторая «равномерность» показателей по всем локальным критериям. Используют следующие реализации принципа равномерности:
Принцип равенства формально выражается следующим образом:
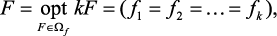
то есть оптимальным считается вариант, принадлежащий области компромиссов, при котором все значения локальных критериев равны между собой. Однако случай f1 = f2 = … = fk может не попасть в область компромиссов или вообще не принадлежать к области допустимых вариантов.
Принцип максимина формально выражается следующим образом:
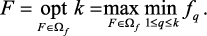
В случае применения этого принципа из области компромиссов выбирается вариант с минимальными значениями локальных критериев и среди них ищется вариант, имеющий максимальное значение. Равномерность в этом случае обеспечивается за счёт «подтягивания» критерия с наименьшим уровнем.
Принцип квазиравенства заключается в том, что стремятся достичь приближённого равенства всех локальных критериев. Приближение характеризуется некоторой величиной β. Это принцип может быть использован в дискретном случае.
Следует отметить, что принципы равенства, несмотря на их привлекательность, не могут быть рекомендованы во всех случаях. Иногда даже небольшое отклонение от равномерности может дать значительный прирост одному из критериев.
Принцип справедливой уступки основан на сопоставлении и оценке прироста и убыли величины локальных критериев. Переход от одного варианта к другому, если они оба принадлежат области компромиссов, неизбежно связан с улучшением по одним критериям и ухудшением по другим. Сопоставление и оценка изменения значения локальных критериев может производиться по абсолютному значению прироста и убыли критериев (принцип абсолютной уступки), либо по относительному (принцип относительной уступки).
Принцип абсолютной уступки может быть формально выражен с помощью следующей записи:
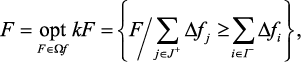
где J+ – подмножество мажорируемых критериев, то есть таких, для которых Δfj > 0; I– – подмножество минорируемых критериев, то есть таких, для которых Δfj < 0; Δfj, Δfj – абсолютное значение приращения критериев; / – символ «такой, для которого».
Таким образом, целесообразным считается выбрать такой вариант, для которого абсолютное значение суммы снижения одного или нескольких критериев не превосходит абсолютное значение суммы повышения оставшихся критериев. Можно показать, что принципу абсолютной уступки соответствует модель максимизации суммы критериев:
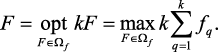
Недостатком принципа абсолютной уступки является то, что он допускает резкую дифференциацию уровней отдельных критериев, так как высокое значение интегрального критерия может быть получено за счёт высокого уровня одних локальных критериев при сравнительно малых значениях других критериев.
Принцип относительной уступки может быть записан в виде:
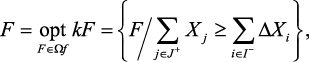
где 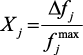 :
: 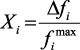 – относительные изменения критериев;
– относительные изменения критериев; 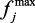 ,
, 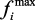 – максимальные значения критериев.
– максимальные значения критериев.
Целесообразно выбрать тот вариант, при котором суммарный относительный уровень снижения одних критериев меньше суммарного относительного уровня повышения других критериев.
Можно сказать, что принципу относительной уступки соответствует модель максимизации произведения критериев
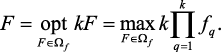
Принцип относительной уступки весьма чувствителен к величине критериев, причём за счёт относительности уступки происходит автоматическое снижение «цены» уступки для локальных критериев с большой величиной и наоборот. В результате проводится значительное сглаживание уровней локальных критериев. Важным преимуществом принципа относительной уступки является также то, что он инвариантен к масштабу изменения критериев, то есть его использование не требует предварительной нормализации локальных критериев.
Принцип выделения одного оптимизируемого критерия формально может быть записан следующим образом:
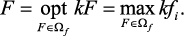
где fi – оптимизируемый критерий при условиях: 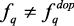 :
: 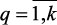 : i ≠ q:
: i ≠ q: 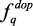 – допустимое значение критерия.
– допустимое значение критерия.
Один из критериев является оптимизируемым и выбирают тот вариант, при котором достигается максимум этого критерия. На другие критерии накладываются ограничения.
Принцип последовательной уступки. Предположим, что локальные критерии расположены в порядке убывающей важности: сначала основной критерий f1, затем другие, вспомогательные критерии f2, f3,… Как и ранее, считаем, что каждый их них нужно обратить в максимум. Процедура построения компромиссного решения сводится к следующему. Сначала находят решение, обращающее в максимум главный критерий f1. Затем, исходя из практических соображений, например, из точности, с которой известны исходные данные, назначают некоторую «уступку» Δf1, допустимую для того, чтобы обратить в максимум второй критерий f2. Налагаем на критерий f2 требование, чтобы он был меньше, чем 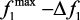 , где
, где 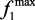 – максимально возможное значение f1 и при этом ограничении ищем вариант, обращающий в максимум f2. Далее снова назначают «уступку» в критерии f2, ценой которой можно макси-
– максимально возможное значение f1 и при этом ограничении ищем вариант, обращающий в максимум f2. Далее снова назначают «уступку» в критерии f2, ценой которой можно макси-
мизировать f3 и т.д.
Такой способ построения компромиссного решения хорош тем, что здесь отчётливо видно, ценой какой «уступки» в одном критерии приобретается выигрыш в другом. Свобода выбора решения, приобретаемая ценой даже незначительных «уступок», может оказаться существенной, так как в районе максимума обычно эффективность решения меняется очень слабо.
Ранее предполагалось, что лучшим считается большее значение локальных критериев, то есть решалась задача максимизации интегрального критерия.
В том случае, если лучшим считается меньшее значение критериев, то от задачи максимизации следует перейти к задаче минимизации. Если ряд критериев необходимо максимизировать, а остальные минимизировать, то для выражения интегрального критерия можно использовать соотношение:
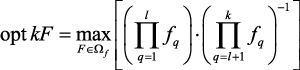
либо
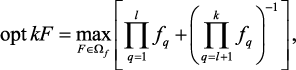
где fq, 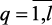 – локальные критерии, которые необходимо максимизировать; fq,
– локальные критерии, которые необходимо максимизировать; fq, 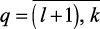 – локальные критерии, которые необходимо минимизировать.
– локальные критерии, которые необходимо минимизировать.
В некоторых случаях минимизируемые критерии удаётся заменить на обратные им, и тогда решается только задача максимизации. Важным этапом решения рассматриваемой задачи является этап нормализации критериев, а также задания и учёта их приоритетов.
Проблема нормализации критериев возникает во всех задачах векторной оптимизации, в которых локальные критерии оптимальности имеют различные единицы измерения. Исключение составляют те задачи, в которых в качестве схемы компромисса применяется принцип относительной уступки.
В основу нормализации критериев положено понятие «идеального вектора», то есть вектора с «идеальными» значениями параметров 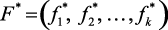 .
.
В нормализованном пространстве критериев вместо действительного значения критерия fq рассматривается безразмерная величина: 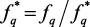 ,
, 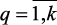 .
.
Если лучшим считается большое значение критерия и если 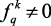 , то
, то 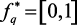 .
.
Успешное решение проблемы нормализации во многом зависит от того, насколько правильно и объективно удаётся определить идеальные значения 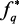 . Способ выбора идеального вектора fи и определяет способ нормализации. Рассмотрим основные способы нормализации.
. Способ выбора идеального вектора fи и определяет способ нормализации. Рассмотрим основные способы нормализации.
● идеальный вектор определяется заданными величинами критериев: Fи = Fзад = {fзад}, 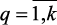 . Недостатком этого способа является сложность и субъективность назначения Fзад, что приводит к субъективности оптимального решения.
. Недостатком этого способа является сложность и субъективность назначения Fзад, что приводит к субъективности оптимального решения.
● в качестве идеального вектора выбирают вектор, параметрами которого являются максимально возможные значения локальных критериев: 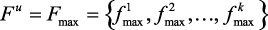 . Недостатком этого способа является то, что он существенно зависит от максимально возможного уровня локальных критериев. В результате равноправие критериев нарушается и предпочтение автоматически отдаётся варианту с наибольшим значением локального критерия.
. Недостатком этого способа является то, что он существенно зависит от максимально возможного уровня локальных критериев. В результате равноправие критериев нарушается и предпочтение автоматически отдаётся варианту с наибольшим значением локального критерия.
● в качестве параметров идеального вектора принимают максимально возможный разброс соответствующих локальных критериев, то есть 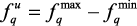 ,
, 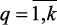 .
.
Известны и другие способы нормализации. Нормализация критериев по существу является преобразованием пространства критериев, в котором задача выбора варианта приобретает большую ясность.
Способы задания и учёта приоритета критериев. Приоритет локальных критериев может быть задан с помощью ряда приоритета, вектора приоритета, весового вектора.
Ряд приоритета 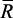 является упорядоченным множеством индексов локальных критериев
является упорядоченным множеством индексов локальных критериев 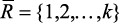 , критерии, индексы которых стоят слева, доминируют над критериями, индексы которых стоят справа. При этом доминирование является качественным: критерий f1 всегда более важен, чем f2 и т.д. В этом случае, если среди критериев имеются равноприоритетные, они выделяются в ряде приоритета скобками, например:
, критерии, индексы которых стоят слева, доминируют над критериями, индексы которых стоят справа. При этом доминирование является качественным: критерий f1 всегда более важен, чем f2 и т.д. В этом случае, если среди критериев имеются равноприоритетные, они выделяются в ряде приоритета скобками, например: 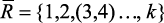 .
.
Приоритет критериев может быть задан вектором приоритета: G = {g1, g2,…, gk} компоненты которого представляют собой отношения, определяющие степень относительного превосходства по важности двух соседних критериев из ряда приоритетов, а именно: величина λq определяет, на сколько критерий fq важнее критерия fq + 1. Если некоторые критерии fq и fq + 1 равнозначны, то соответствующая компонента gq = 1. Для удобства вычислений обычно полагают gk = 1. Вектор приоритета G определяется в результате попарного сравнения локальных критериев, предварительно упорядоченных в соответствии с рядом приоритета 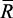 . Очевидно, что любая компонента вектора приоритета удовлетворяет соотношению: gq ≥ 1, q = 1, …, k.
. Очевидно, что любая компонента вектора приоритета удовлетворяет соотношению: gq ≥ 1, q = 1, …, k.
Весовой вектор: b = {b1, b2, …, bk} представляет собой k-мерный вектор, компоненты которого связаны соотношениями:
0 ≤ bq ≤ 1, 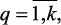
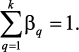
Компонента bq вектора b имеет смысл весового коэффициента, определяющего относительное превосходство критерия fq над всеми остальными. Компоненты векторов G, b связаны соотношениями gq = bq/bq + 1.
Приоритет критериев проще задавать с помощью вектора приоритета, поскольку его компоненты определяются сравнением важности только двух соседних критериев, а не всей совокупности критериев, как при задании весового вектора. Причем это удобно делать последовательно, начиная с последней пары критериев, положив gk = 1. Можно показать, что при gk = 1
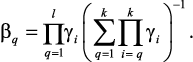
Если приоритет критериев задан в виде ряда, то при выборе оптимального варианта применяют принцип «жесткого приоритета», при котором осуществляется последовательная оптимизация. При этом не допускается повышение уровня критериев с низкими приоритетами, если происходит хотя бы небольшое снижение значения критерия с более высоким приоритетом.
Если заданы вектор приоритета Г или весовой вектор b, то при выборе оптимального варианта можно использовать принцип «гибкого приоритета». При этом оценка варианта производится по взвешенному векторному критерию, где в качестве компонент вектора критериев
{f1, f2, …, fk} используются компоненты вектора {b1f1, b2f2, …, bkfk}. В этом случае могут быть применимы все рассмотренные принципы выбора варианта в области компромиссов (принцип равенство, справедливой уступки и т.д.) с заменой fq на bqfq.
Примером многокритериальной задачи принятия решений может служить рассмотренная ранее задача выбора оптимального режима работы блока риформинга в следующей интерпретации. Оптимальный режим работы объекта характеризуются следующими локальными критериями: объемом выходной продукции – катализата – f1, октановое число продукции – f2, стабильность катализатора – f3 и т.п. Пусть для ЛПР эти локальные критерии в данной ситуации имеют следующую относительную важность: g1, g2, g3, и т.д. соответственно. Тогда при использовании метода абсолютной уступки для случая трех локальных критериев лучшим будет такой режим работы, для которого:
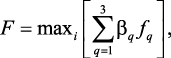
где i – i-й режим работы блока риформинга, i = 1, …, n.
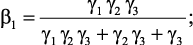
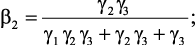
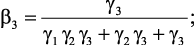
γ3 = 1.
Таким образом, принятие решений – это наука и искусство. Роль принятого решения огромна. Важнейший вопрос успешного функционирования организации заключается в том, как организация может выявлять свои проблемы и решать их. Каждое решение нацелено на какую-то проблему, а правильное решение – это то, которое максимально обеспечивает цели организации.
