
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.1. Динамические характеристики аналоговых систем
Для оценки динамических свойств аналоговых систем или отдельных звеньев исследуется их реакции на типовые входные воздействия. Рассмотрим случай, когда на вход устройства, например, электрической цепи, поступает единичный ступенчатый сигнал
x(t) = 1(t), (1.1)
где 1(t) – единичная ступенчатая функция, удовлетворяющая условию
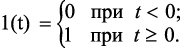 (1.2)
(1.2)
Преобразование Лапласа единичной ступенчатой функции равно
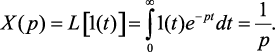 (1.3)
(1.3)
Преобразование Лапласа для выходного сигнала устройства при нулевых начальных условиях имеет вид
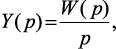 (1.4)
(1.4)
где 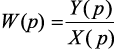 передаточная функция электрической цепи.
передаточная функция электрической цепи.
Реакцию электрической цепи на единичное ступенчатое воздействие называют переходной функцией
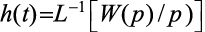 . (1.5)
. (1.5)
Переходная функция вычисляется по формуле обращения
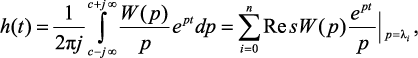 (1.6)
(1.6)
где λi – полюсы подинтегрального выражения; n – число полюсов.
Вычет в простом полюсе вычисляется по формуле
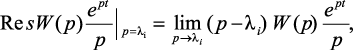 (1.7)
(1.7)
а в полюсе кратности к
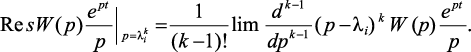 (1.8)
(1.8)
Если действие единичной ступенчатой функции начинается в момент времени t = τ, то она принимает вид
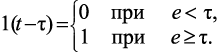 (1.9)
(1.9)
Единичное ступенчатое воздействие довольно легко реализуется и поэтому широко используется в экспериментальных исследованиях динамических свойств электротехнических и электронных устройств. Графики единичной ступенчатой функции и переходной функции изображены на рис. 1.1.
Рассмотрим случай, когда на вход устройства поступает единичная импульсная функция (функция Дирака):
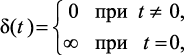
для которой выполняется условие
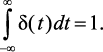 (1.10)
(1.10)
Функцию δ(t) можно представить как бесконечно большой импульс в момент t = 0, площадь которого равна единице. Это воздействие, как и предыдущее, является довольно тяжелым для исследуемых объектов.
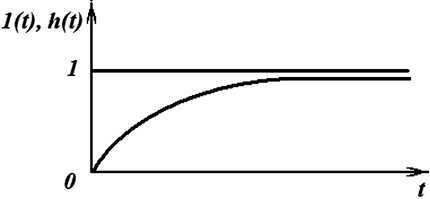
Рис. 1.1. Единичное ступенчатое воздействие и переходная функция
Так как преобразование Лапласа для δ-функции равно единице, то выходной сигнал цепи определяется выражением
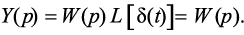 (1.11)
(1.11)
Реакцию системы на действие единичного импульса называют импульсной переходной функцией k(t). Из выражения (1.11) следует, что
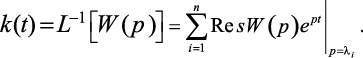 (1.12)
(1.12)
Импульсная переходная функция электрической цепи удовлетворяет следующим условиям:
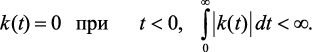 (1.13)
(1.13)
Первое условие называют условием физической реализуемости, оно показывает, что в реальной устройстве переходный процесс не может возникнуть раньше подачи на вход единичного импульса. Второе условие вытекает из условия устойчивости. Согласно выражениям (1.5) и (1.12)
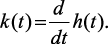 (1.14)
(1.14)
Запись δ(t – τ) означает, что единичный импульс приложен в момент времени τ. Поэтому, например,
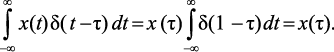 (1.15)
(1.15)
В реальных электротехнических и электронных устройствах единичный импульс имеет конечную длительность τ, которая должна удовлетворять условию
τ << Тmin, (1.16)
где Тmin – наименьшая из постоянных времени передаточной функции W(p) устройства. Единичный импульс можно представить прямоугольным импульсом, длительность которого равна τ, амплитуда – 1/τ. Кроме того, единичный прямоугольный импульс можно представить как разность двух ступенчатых функций (рис. 1.2):
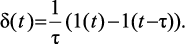 (1.17)
(1.17)
Рассмотрим влияние длительности единичного импульса τ на реакцию электрической цепи [59]. Пусть реакция на ступенчатое воздействие 1(t)/τ определяется выражением
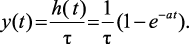 (1.18)
(1.18)
Определим, на какую величину возрастет функция у(t) за время τ. Поскольку τ << Т (T = 1/а), то на интервале 0...τ функция y(t) близка к линейной (рис. 1.2)
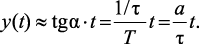 (1.19)
(1.19)
Тогда при t = τ
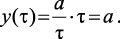 (1.20)
(1.20)
Аналогично определяется значение функции y(t) для единичного импульса с длительностью τ/2 и с амплитудой 2/τ
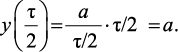 (1.21)
(1.21)
Таким образом, при условии τ << Т, реакция электрической цепи не зависит от длительности импульса, а определяется только его площадью, то есть информация в сигнале δ(t) заключена не в амплитуде, а в его
площади (аналогичное явление в теории механических систем – удар). Следовательно, не нарушая принципа действия устройства и режима работы электрической цепи, можно выбрать удобную форму импульса с площадью, равной единице. На рис. 1.3 представлены различные формы δ(t)-функции, которые вызывают одинаковую реакцию k(t).
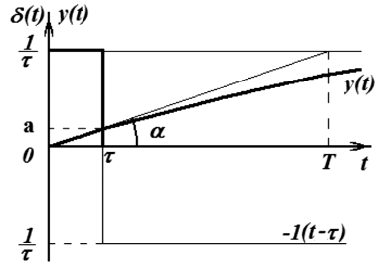
Рис. 1.2. Импульсное воздействие δ(t) и реакция y(t)
Если площадь импульса отлична от единицы в Q раз, то и реакция отличается тоже в Q раз
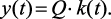 (1.22)
(1.22)
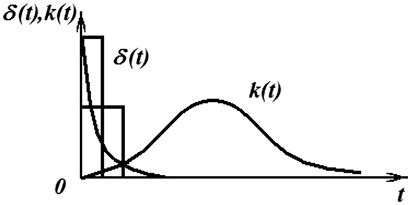
Рис. 1.3. Различные формы δ-функции и реакция k(t)
